ax²+bx+c=0(a≠0),其中 ![]() 是二次项,
是二次项, ![]() 是二次项系数;
是二次项系数; ![]() 是一次项;
是一次项; ![]() 是一次项系数;
是一次项系数; ![]() 是常数项。
是常数项。
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根
参考:百度百科
-------一元二次方程的解(根)--------
ax²+bx+c=0(a≠0)
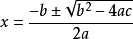
-----------------------------------------------------------
据判别式计算有几个根:
① 当  时,方程有两个不相等的实数根;
时,方程有两个不相等的实数根;
② 当  时,方程有两个相等的实数根;
时,方程有两个相等的实数根;
③ 当  时,方程无实数根,但有2个共轭复根。
时,方程无实数根,但有2个共轭复根。
上述结论反过来也成立。
---------------------------------------------------------
韦达定理(两根关系)
设一元二次方程 
 中,两根
中,两根  有如下关系:
有如下关系:
推导如下:
由一元二次方程求根公式知:

则有:
一元二次方程变形式
 (
(  是实数,
是实数,  )
)
--------------------------------------------------
配方式
----------------------------------------------------
两根式-------------------------------------------------------