树状数组学习笔记

定义

树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。 —— by baidu

实现

用一个数组$bit[i]$表示从$[i - lowbit(x) + 1, x]$中的所有的数的和。
如下图：

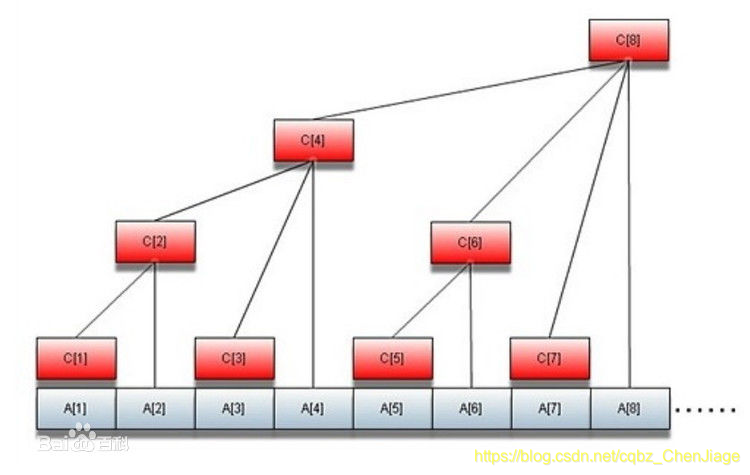
lowbit操作

$lowbit$表示一个数在二进制中只保留最后一位1及其以后的0所表示的数字。
常用的方法：
先将原数取反再与上原数：

int lowbit(int x) {
	return x & (-x);
}

update操作

$update$是单点修改操作，可以修改任意一个点上的数值，并进行全局维护。

void update(int x, int y) {
	for(int i = x;i <= n; i += lowbit(i)) 
		bit[i] += y;
}

Sum操作

$Sum(x)$是将从$1 -x$的所有数值的和累加起来：

long long Sum(int x) {
	long long ans = 0;
	for(int i = x; i; i -= lowbit(i))
		ans += bit[i];
	return ans;
}

常用模板

单点修改，区间查询

基本操作

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1e6 + 5;

int n, q;
long long a, bit[MAXN];

int lowbit(int x) {
	return x & (- x);
}

long long Sum(int x) {
	long long ans = 0;
	for(int i = x;i > 0; i -= lowbit(i)) ans += bit[i];
	return ans;
}

void update(int x, int y) {
	for(int i = x;i <= n; i += lowbit(i)) bit[i] += y;
}

int main() {
	scanf("%d %d", &n, &q);
	for(int i = 1;i <= n; i++) {
		scanf("%lld", &a);
		update(i, a);
	}
	for(int i = 1;i <= q; i++) {
		int oder;
		scanf("%d", &oder);
		if(oder == 1) {
			int k, x;
			scanf("%d %d", &k, &x);
			update(k, x);
		} 
		if(oder == 2) {
			int l, r;
			scanf("%d %d", &l, &r);
			printf("%lld
", Sum(r) - Sum(l - 1));
		}
	}
	return 0;
} 

区间修改，区间查询

$P[]仍为A[]的差分数组，那么原数组的前缀和 A[1]+A[2]+……+ A[n] =P[1]+(P[1]+P[2])+(P[1]+P[2]+P[3])+……+(P[1]+P[2]+……+P[n]) =n*P[1]+(n-1)*P[2]+(n-2)*P[3]+……+P[n] =n*(P[1]+P[2]+P[3]+……+P[n])-(0*P[1]+1*P[2]+2*P[3]+……+(n-1)*P[n])$
观察减式两边，分别将P[i]和(i-1)p[i]建立两个树状数组BIT1和BIT2，BIT1就是差分数组，区间修改按上一例进行；BIT2的增量就不是x了，而是x*(i-1)。至于区间查询，我们已经知道原数组前缀和了，直接相减即可查询区间和。

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1e6 + 5;

int n, q;
int a[MAXN];
long long bit1[MAXN], bit2[MAXN];

int lowbit(int x) {
	return x & -x;
}

void updata(int x, int y) {
	for(int i = x;i <= n; i += lowbit(i)) {
		bit1[i] += (long long) y;
		bit2[i] += (long long) (x - 1) * y;
	}
}

long long Sum(int k) {
	long long ans = 0;
	for(int i = k; i; i -= lowbit(i)) {
		ans += (long long) bit1[i] * k - (long long) bit2[i];
	}
	return ans;
}

int main() {
	scanf("%d %d", &n, &q);
	for(int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
		updata(i, a[i] - a[i - 1]);
	}
	for(int i = 1;i <= q; i++) {
		int opt, l, r, x;
		scanf("%d", &opt);
		if(opt == 1) {
			scanf("%d %d %d", &l, &r, &x);
			updata(l, x);
			updata(r + 1, -x);
		} 
		if(opt == 2) {
			scanf("%d %d", &l, &r);
			printf("%lld
", Sum(r) - Sum(l - 1));
		}
	}
	return 0;
} 

区间修改，单点查询

$对原数组A[]建一个差分数组P[i]=A[i]-A[i-1]那么A[i]=P[1]+P[2]+……+P[i]$
将差分数组P[]建立BIT，单点查询就是sum，区间修改就是update(left, x)和update(right+1, -x)，BIT求前缀和sum就是区间修改后的单点查询了。

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1e6 + 5;

int n, q, a[MAXN];
long long p[MAXN], bit[MAXN];

int lowbit(int x) {
	return x & (- x);
}

void updata(int x, int y) {
	for(int i = x;i <= n; i += lowbit(i)) bit[i] += y;
}

long long Sum(int x) {
	long long ans = 0;
	for(int i = x;i > 0; i -= lowbit(i)) {
		ans += bit[i];
	}
	return ans;
}

int main() {
	scanf("%d %d", &n, &q);
	for(int i = 1;i <= n; i++) {
		scanf("%d", &a[i]);
		p[i] = a[i] - a[i - 1];
		updata(i, p[i]);
	}
	for(int i = 1;i <= q; i++) {
		int oder;
		scanf("%d", &oder);
		if(oder == 1) {
			int l, r, x;
			scanf("%d %d %d", &l, &r, &x);
			updata(l, x);
			updata(r + 1, -x);
		} else {
			int x;
			scanf("%d", &x);
			printf("%lld
", Sum(x));
		}
	}
	return 0;
}

二维树状数组 ：单点修改，区间查询

#include <map>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1e4 + 5; 

int n, m, opt;
long long bit[MAXN][MAXN];

int lowbit(int x) {
    return x & -x;
}

void update(int x, int y, int k) {
	for(int i = x; i <= n; i += lowbit(i)) {
		for(int j = y; j <= m; j += lowbit(j)) {
			bit[i][j] += k;
		}
	}
}

long long Sum(int x, int y) {
	long long ans = 0;
	for(int i = x; i > 0; i -= lowbit(i)) {
		for(int j = y; j > 0; j -= lowbit(j)) {
			ans += bit[i][j];
		}
	}
	return ans;
}

int main() {
	scanf("%d %d", &n, &m);
	while(scanf("%d", &opt) != EOF) {
		if(opt == 1) {
			int x, y, k;
			scanf("%d %d %d", &x, &y, &k);
			update(x, y, k);
		} else {
			int a, b, c, d;
			scanf("%d %d %d %d", &a, &b, &c, &d);
			printf("%lld
", Sum(c, d) - Sum(a - 1, d) - Sum(c, b - 1) + Sum(a - 1, b - 1));
		} 
	}
	return 0;
}
 

二维树状数组 ：区间修改，区间查询

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#define LL long long
using namespace std;
const int MAXN = 2055;

int n, m, arr[MAXN], opt;
long long bit1[MAXN][MAXN], bit2[MAXN][MAXN], bit3[MAXN][MAXN], bit4[MAXN][MAXN];

int lowbit(int x) { return x & -x; }

void update(int a, int c, int x) {
    for (int i = a; i <= n; i += lowbit(i)) {
        for (int j = c; j <= m; j += lowbit(j)) {
            bit1[i][j] += (LL)x;
            bit2[i][j] += (LL)c * x;
            bit3[i][j] += (LL)a * x;
            bit4[i][j] += (LL)a * c * x;
        }
    }
}

long long Sum(int x, int y) {
    long long ans = 0;
    for (int i = x; i; i -= lowbit(i)) {
        for (int j = y; j; j -= lowbit(j)) {
            ans += (LL)bit1[i][j] * (x + 1) * (y + 1) - (LL)bit2[i][j] * (x + 1) - (LL)bit3[i][j] * (y + 1) +
                   (LL)bit4[i][j];
        }
    }
    return ans;
}

int main() {
    scanf("%d %d", &n, &m);
    while (scanf("%d", &opt) != EOF) {
        int a, b, c, d, x;
        if (opt == 1) {
            scanf("%d %d %d %d %d", &a, &b, &c, &d, &x);
            update(a, b, x);
            update(c + 1, b, -x);
            update(a, d + 1, -x);
            update(c + 1, d + 1, x);
        }
        if (opt == 2) {
            scanf("%d %d %d %d", &a, &b, &c, &d);
            printf("%lld
", Sum(c, d) + Sum(a - 1, b - 1) - Sum(a - 1, d) - Sum(c, b - 1));
        }
    }
    return 0;
}