朴素贝叶斯算法,点进来了解了解。

还请大家多多指点，一起进步喔。

贝叶斯方法是以贝叶斯原理为基础，使用概率统计的知识对样本数据集进行分类。由于其有着坚实的数学基础，贝叶斯分类算法的误判率是很低的。贝叶斯方法的特点是结合先验概率和后验概率，即避免了只使用先验概率的主管偏见，也避免了单独使用样本信息的过拟合现象。贝叶斯分类算法在数据集较大的情况下表现出较高的准确率，同时算法本身也比较简单。

朴素贝叶斯法（NPC）是基于贝叶斯定理与特征条件独立假设的分类方法。
NBC模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，这给NBC模型的正确分类带来了一定影响,这也是缺点所在。

先认识一下朴素贝叶斯的优缺点：
优点：
朴素贝叶斯算法假设了数据集属性之间是相互独立的，因此算法的逻辑性十分简单，并且算法较为稳定，当数据呈现不同的特点时，朴素贝叶斯的分类性能不会有太大的差异。换句话说就是朴素贝叶斯算法的健壮性比较好，对于不同类型的数据集不会呈现出太大的差异性。当数据集属性之间的关系相对比较独立时，朴素贝叶斯分类算法会有较好的效果。
缺点：
属性独立性的条件同时也是朴素贝叶斯分类器的不足之处。数据集属性的独立性在很多情况下是很难满足的，因为数据集的属性之间往往都存在着相互关联，如果在分类过程中出现这种问题，会导致分类的效果大大降低。

贝叶斯算法属于有监督的分类算法

思想 ： 通过已知类别的训练数据集，计算样本的先验概率，然后利用贝叶斯公式概率公式测算未知类别样本属于某个类别的后验概率， 最终以最大后验概率所对应的样本类别作为样本的预测值。

由全概率公式以及概率乘法可得 贝叶斯公式，y = f(x) = P(CiX)/P(X) = (P(Ci)*P(X|Ci))/sum(P(Ci)*P(X|Ci)) i=1,2,3,4,5,…

最后取argmax y = argmax f(x) = argmax P(CiX)/P(X) 作为最大后验概率值（一般转换成计算分子的最大值，因为分子求和公式说明了分子是一个常量）。
如果 分子中P(Ci)未知的话，一般会假设每个类别出现的概率相等，只需计算P(X|Ci)的最大值。大多数情况下P(Ci)是以训练数据集中类别Ci的频率作为先验概率。

现在只剩下分子中的P(X|Ci)待求，就是已知类别的情况下自变量X为某种值的概率。因为计算条件概率（这里是联合概率）比较费时、复杂，
这时一般假设自变量是条件独立的: 即 P(X|Ci) = P(x1,x2,x3…xp|Ci) = P(x1|Ci)* P(x2|Ci)* P(x3|Ci)… P(xp|Ci)；但是同时也就产生了缺点。

总结三种常见的朴素贝叶斯分类器：

一、高斯贝叶斯分类器

如果数据集中的自变量X均为连续的数值型，则在计算P(X|Ci)是会假设自变量X服从高斯正太分布，

所以自变量X的条件分布表示为：P(Xj|Ci) = 1/(Qji * sqrt(2Pi,1/2)) * exp(-(Xj-Uji)**2 / 2Qji**2)

Qji是训练数据集中自变量Xj属于类别Ci的标准差、Uji是训练数据集中自变量Xj属于类别Ci的均值，Xj表示第j个自变量的取值。
一个例子：
有如下的数据集，假设某金融公司是否愿意放贷给客户会优先考虑两个因素，分别是年龄和收入。

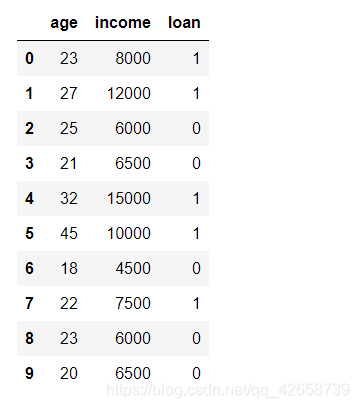
现在有一位客户年龄24岁，收入为8500元，问公司是否愿意给客户放贷？

则计算步骤如下：（解释、解答是否愿意给该客户放贷）

1. 因变量各类别的频率：

P(loan=0) = 5/10 = 0.5

P(loan=1) = 5/10 = 0.5

2. 求非标签字段的字段的各两个标签下的均值与标准差：

均值：

Uage0 = (25+21+18+23+20)/5 = 21.40

Uage1 = (23+27+32+45+22)/5 = 29.8

Uincome0 = (6000+6500+4500+6000+6500)/5 = 5900

Uincome1 = (8000+12000+15000+10000+7500)/5 = 10500

标准差：

Qage0 = (((25-21.40)**2+(21-21.40)**2+(18-21.40)**2+(23-21.40)**2+(20-21.40)2)/5)(1/2) = 2.416 == 2.42

Qage1 = 8.38

Qincome0 = 734.85

Qincome1 = 2576.81

3 单变量的条件概率

P(age =24|loan=0) = 1/(Qji * sqrt(2Pi,1/2)) * exp(-(Xj-Uji)**2 / 2Qji**2) = 0.0926

P(age=24|loan=1) = 0.0375

P(income=8500|loan=0) = 1.0384 * (10**(-6))

P(income=8500|loan=1) = 1.1456 * (10**(-4))

4. 计算后验概率：

【(1.)计算在age=0和income=8500这两个事件同时发生的情况下,loan=0的概率】

P(loan=0|(age=24,income=8500)) = P(loan=0)P(age=24|loan=0)P(income=8500|loan=0) = 4.8079(10*(-8))

【(2.)计算在age=0和income=8500这两个事件同时发生的情况下,loan=1的概率】

P(loan=1|(age=24,income=8500)) = P(loan=1)P(age=24|loan=1)P(income=8500|loan=1) = 2.1479(10*(-6))

所以，当age=24和income=8500时，被预测为不放贷的概率为 4.8079*(10**(-8))。被预测为放大的概率为2.1479*(10**(-6))。根据最大后验数的原则，公司决定给该客户放贷。

一个demo解释（利用伯努利贝叶斯分类器实现面部皮肤区分的判别）

实现高斯贝叶斯分类器，在sklearn中有naive_bayes模块中的GaussianNB类。
该类只有一个参数 naive_bayes.GaussianNB(priors=None) ，
priors用于指定因变量各类别的先验概率，默认以数据集中的类别频率作为先验概率。

该数据集含有两部分，一部分是人类面部皮肤数据，该部分数据是由不同种族、年龄、和性别人群的图片转换而成的；另一部分是非人类面部皮肤数据。‘
两个部分的数据集一共包含245057条样本和4个变量，自变量为R、G、B，代表图片中的三原色。因变量为y，属于二分类变量，1表示人类面部皮肤（正例）
首先使用pandas库读入数据并且查看数据的大体结构和信息：

查看数据集是否有空值：skin.isnull().any()

# 设置正例和负例
skin.y = skin.y.map({2:0,1:1})  #把是2的设置为0（负例），把是1的设置为1（正例）
skin.y.value_counts()
#把数据转成浮点型
skin = skin.astype(float)

拆分样本建立模型：

# 样本拆分
X_train,X_test,y_train,y_test = model_selection.train_test_split(skin.iloc[:,:3], skin.y, test_size = 0.25,random_state=1234)
# 调用高斯朴素贝叶斯分类器的“类”
gnb = naive_bayes.GaussianNB()

# 模型拟合
gnb.fit(X_train, y_train)

# 模型在测试数据集上的预测
gnb_pred = gnb.predict(X_test)

# 各类别的预测数量
pd.Series(gnb_pred).value_counts()
# 预测为负例（0也就是原数据中的2【非人类面部皮肤】）的有50630，正例有10635

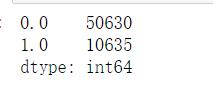
可视化预测效果

1.绘制混淆矩阵：

# 导入第三方包
from sklearn import metrics
import matplotlib.pyplot as plt
import seaborn as sns

# 构建混淆矩阵
cm = pd.crosstab(gnb_pred,y_test)

# 绘制混淆矩阵图
sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd')

# 去除x轴和y轴标签
plt.xlabel('Real')
plt.ylabel('Predict')

# 显示图形
plt.show()

print('模型的准确率为：
',metrics.accuracy_score(y_test, gnb_pred))
print('模型的评估报告：
',metrics.classification_report(y_test, gnb_pred))

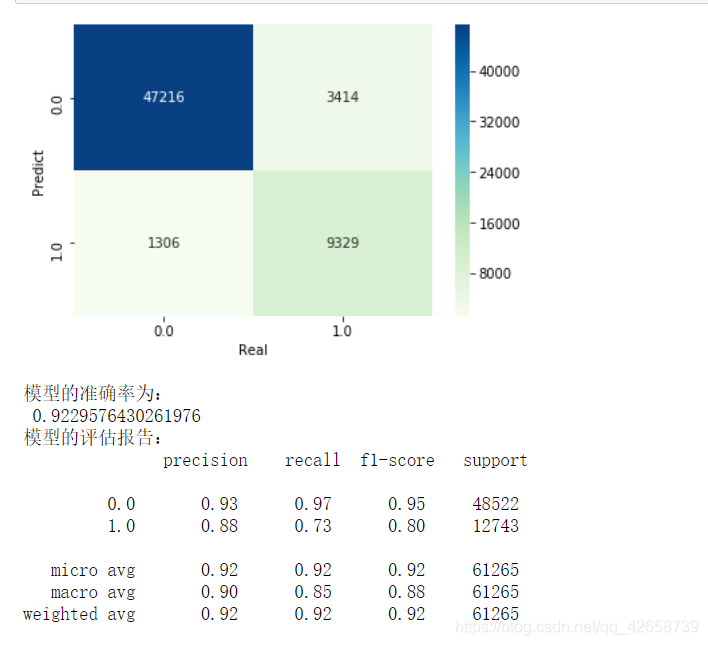
如何去解读这个混淆矩阵和评估报告？
可视化的混淆矩阵中：
左上角第一块深蓝色区域是 表示真实为0预测为0的有47216个样本；
左下角的区域是 表示 真实为0但预测为1的样本有1306个样本；
右上角的区域是 表示 真实为1但预测为0的样本是有3414个样本；
右下角的区域是 表示 真实为1，预测也为1的样本有9329个样本。
知识补充：
True Positive （真正, TP）被模型预测为正的正样本；
True Negative（真负 , TN）被模型预测为负的负样本 ；
False Positive （假正, FP）被模型预测为正的负样本；
False Negative（假负 , FN）被模型预测为负的正样本；

分类准确率分数【对应图中模型准确率】是指所有分类正确的百分比。分类准确率这一衡量分类器的标准比较容易理解，但是它不能告诉你响应值的潜在分布，并且它也不能告诉你分类器犯错的类型。
准确率(Accuracy) = (TP+FN) / （ TP+FN+FP+TN）

metrics的分类评估报告解读：
列表左边上部分的一列为分类的标签名，左边下部分的一列为平均值。
precision 精确率 = TP /(TP+FP)
recall 召回率 = TP / (TP+FN)
f1-score可以看作是模型准确率和召回率的一种加权平均，它的最大值是1，最小值是0,计算公式是F1 = 权值* (准确率 *召回率)/(准确率+召回率)。
support ： 我也不太了解，看图形结合数据的相关可以判断这个是代表对应标签中的真实值个数。

2.绘制ROC曲线，寻找AUC值（>0.8即可认为模型是好的）

# 计算正例的预测概率，用于生成ROC曲线的数据
y_score = gnb.predict_proba(X_test)[:,1]
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)

# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

二、多项式贝叶斯分类器

如果数据集的自变量X都为离散变量时，就无法使用高斯贝叶斯分类器，应该选择多项式贝叶斯分类器。
多项式贝叶斯分类器构造详解：
#在计算概率值P(X|Ci)时，有 P(xj = xjk|Ci) = (Nik+ arf)/(Ni+n*arf)
其中，xjk表示自变量xj的值；Nik表示因变量为类别Ci时自变量xj取xjk的样本个数；Ni表示数据集中类别Ci的样本个数；arf为平滑系数，用于防止概率值取0可能，通常取值为1，表示对概率值做拉普拉斯平滑；n则表示因变量的类别个数。

• 加入平滑系数是为了防止其单变量概率为0，进而导致所求概率为0.

一个例子解释多项式贝叶斯分类器：假设影响女孩是否参加相亲活动的重要因素有三个，分别时男孩的职业、受教育水平和收入状况；
如果女孩参加相亲活动，则对应的Meet变量为1，否则为0.
问：在如下表中给定的信息下，对于高收入的公务员并且其学历为硕士的男生来说，女孩是否愿意参加他的相亲？

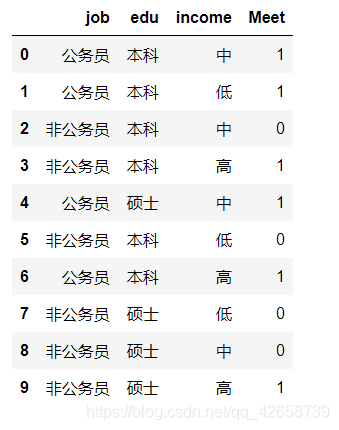
求解：

1. 因变量各类别频率:

   P(Meet=0) = 4/10 = 0.4
   P(Meet=1) = 6/10 = 0.6

2. 单变量条件概率(根据题目所求列出所需的单变量条件概率)：

   P(job=公务员|Meet=0) = (0+1)/(4+21) = 1/6
   P(job=公务员|Meet=1) = (4+1)/(6+21) = 1/8
   P(edu=硕士|Meet=0) = (2+1)/(4+21) = 3/6
   P(edu=硕士|Meet=1) = (2+1)/(4+21) = 3/8
   P(income=高|Meet=0) = (0+1)/(4+21) = 1/6
   P(income=高|Meet=1) = (2+1)/(6+21) = 4/8

3. 寻找贝叶斯后验概率以及最大后验概率：

   P(Meet=0|job=公务员,edu=硕士，income=高) = P(Meet=0)P(job=公务员|Meet=0)P(edu=硕士|Meet=0)P(income=高|Meet=0)=0.4(1/6)(3/6)(1/6)=1/180
   
   P(Meet=1|job=公务员,edu=硕士，income=高) = 18/256

所以，根据最大后验概率原则，愿意见面的概率（18/256）>不愿见面的概率(1/180)，所以，该女生选择参加这位男生的相亲。

一个demo解释：
根据蘑菇的各项特征判断其是否有毒
因变量为type表示是否有毒，剩余的自变量是关于蘑菇的一些特征。

如何快速实现多项式贝叶斯分类器提高工作效率？？？ 如下类实现：

  naive_bayes.MultinomialNB(alpha=1.0,fit_prior=True,class_prior=None) 

1. alpha是用于指定平滑系数的值，默认为1.0
2. fit_prior是布尔类型的参数，意思是是否以数据集中各类别(标签)的比例作为P(Ci)的先验概率，默认为True。
3. class_prior是用于人工指定各类别的先验概率P(Ci)。如果指定该参数，则fit_prior为false或者不再为true或者不再有效。

查看数据的信息：

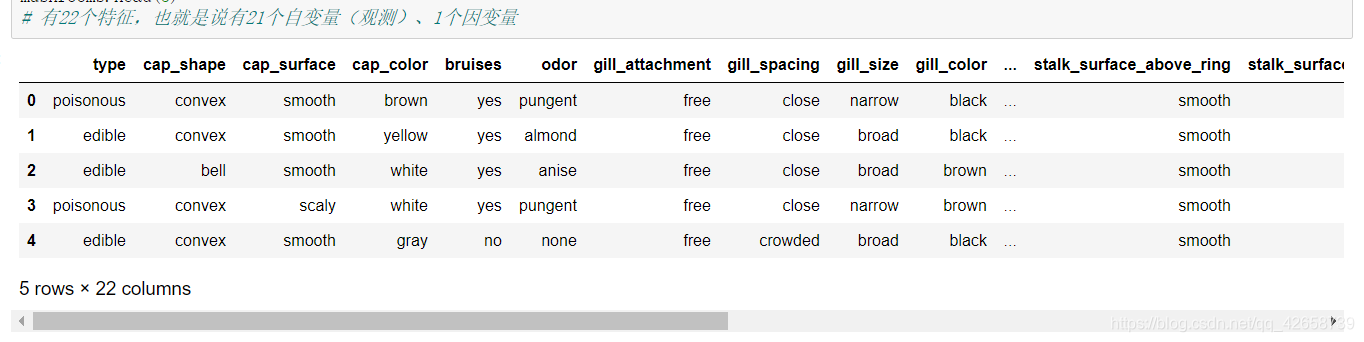
表中所有变量均为字符型离散变量，由于python建模过程必须要求自变量为数值类型，所以需要做因子化处理，即把字符值转化为对应的数值。

columns = mushrooms.columns[1:]
for column in columns:
    mushrooms[column] = pd.factorize(mushrooms[column])[0]
    #因子化处理时factorize()函数返回一个元组，元组的第一个元素是转换成的数值、第二个元素是数值对应的字符水平
mushrooms.head(5)

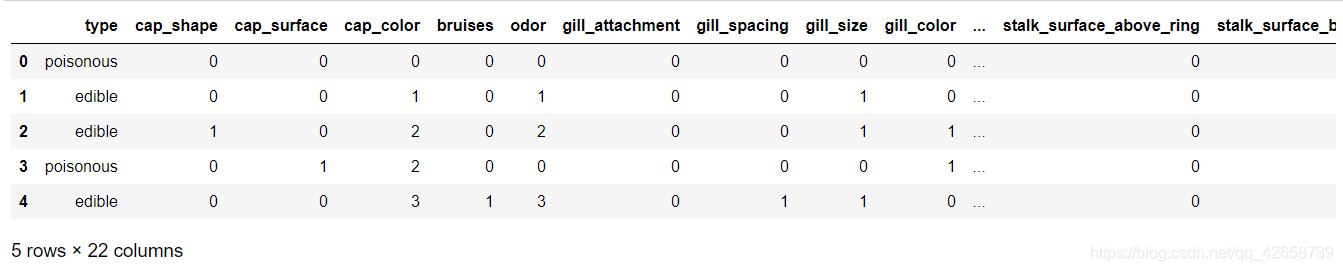
拆分数据并建立模型：

# 将数据集拆分为训练集合测试集
Predictors = mushrooms.columns[1:]
X_train,X_test,y_train,y_test = model_selection.train_test_split(mushrooms[Predictors], mushrooms['type'],  test_size = 0.25, random_state = 10)

# 建立模型
from sklearn import metrics
import seaborn as sns
import matplotlib.pyplot as plt

# 构建多项式贝叶斯分类器的“类”
mnb = naive_bayes.MultinomialNB()

# 基于训练数据集的拟合
mnb.fit(X_train, y_train)

# 基于测试数据集的预测
mnb_pred = mnb.predict(X_test)
 #到此为此

三、伯努利贝叶斯分类器

当数据集的自变量X均为0-1二元值时（例如在文本挖掘中判断某个词语是否出现在句子中，出现用1表示，不出现用0表示），通常优先选择伯努利贝叶斯。

利用伯努利贝叶斯计算概率值P(X|Ci)时，会假设自变量X的条件概率满足伯努利分布，故其P(X|Ci)表示为：
P(xj|Ci) = p * xj+(1-p) * (1-xj)

其中，xj为第j个变量，取值为0或者1；
p表示类别为Ci时自变量取1的概率（该概率值可以用经验概率代替）,即 ：

p=P(xj=1|Ci) = (Nxj + arfa)/(Ni+n * arfa)

其中Ni表示类别Ci的样本个数；Nxj表示样本在类别为Ci时，xj变量取1的样本量；arfa为平滑系数；n为因变量中的类别个数。

一个案例解释伯努利贝叶斯:

假设有10条评论数据做分词处理后，得到如下表的文档词条矩阵，矩阵中有5个词语和一个表示情感的结果，其中0表示正面情绪，1表示负面情绪。
问：如果一个用户的评论中包含了“还行”一词，该用户的评论属于哪种情绪？

• 文本挖掘中判断某个词语是否出现在句子中，出现用1表示，不出现用0表示.

求解：

1.计算因变量各类别的频率（作为概率）：

P(类别=0)=4/10 = 0.4
P(类别=1)=6/10 = 0.6

2.使用计算单变量的条件概率：

P(x1=0|类别=0) = (Nxj+arfa)/(Ni+n * arfa) = (1+1)/(4+2) = 1/3
P(x1=0|类别=1) = (4+1)/(6+2) = 5/8
P(x2=0|类别=0) = (1+1)/(4+2) = 1/3
P(x2=0|类别=1) = (4+1)/(6+2) = 5/8
P(x3=0|类别=0) = (4+1)/(4+2) = 5/6
P(x3=0|类别=1) = (1+1)/(6+2) = 1/4
P(x4=1|类别=0) = (2+1)/(4+2) = 1/2
P(x4=1|类别=1) = (0+1)/(6+2) = 1/8
P(x5=0|类别=0) = (4+1)/(4+2) = 5/6
P(x5=0|类别=1) = (1+1)/(6+2) = 1/4

3.使用概率乘法公式计算贝叶斯后验概率:

P(类别=0|x1=0,x2=0,x3=0,x4=1,x5=0) = P(类别=0)* P(x1=0|类别=0) * P(x2=0|类别=0) * P(x3=0|类别=0) * P(x4=1|类别=0) * P(x5=0|类别=0) = 5/324

P(类别=1|x1=0,x2=0,x3=0,x4=1,x5=0) = P(类别=1)* P(x1=0|类别=1) * P(x2=0|类别=1)* P(x3=0|类别=1)* P(x4=1|类别=1) * P(x5=0|类别=1) = 3/4096

所以，用户的评论中只有“还行”一词时，正面评论的概率 > 负面评论的概率，所以预判为正面评论。

一个demo：

对用户的评价数据进行分类，分类的目的是预测用户的评价内容所表达的情绪（积极或者消极）
数据集包含四个字段，分别是用户昵称、评价时间、评价内容、和对应的评价情绪.评价内容中会有一些脏数据。
查看数据信息：

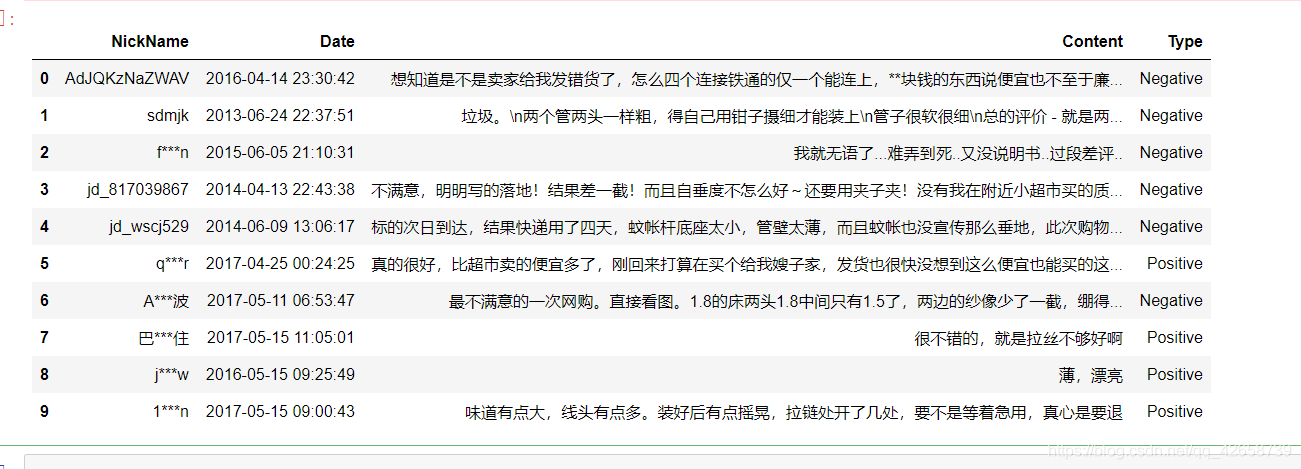
运用正则表达式，将评论中的数字和英文去除

evaluation.Content = evaluation.Content.str.replace('[0-9a-zA-Z]','')
#evaluation.head()

引入自定义词典（词库和停止词词库【使用停止词目的是无用的词语去掉】）对文本进行切词：

import jieba

# 加载自定义词库
jieba.load_userdict(r'all_words.txt')

# 读入停止词
with open(r'mystopwords.txt', encoding='UTF-8') as words:
    stop_words = [i.strip() for i in words.readlines()]

# 构造切词的自定义函数，并在切词过程中删除停止词
def cut_word(sentence):
    words = [i for i in jieba.lcut(sentence) if i not in stop_words]  #切词过程中删除停止词
    # 切完的词用空格隔开
    result = ' '.join(words)
    return(result)

# 对评论内容进行批量切词
words = evaluation.Content.apply(cut_word)
# 前5行内容的切词效果
words[0]

利用切好的词，构造文档词条矩阵，矩阵的每一行代表一个评论内容，矩阵的每一列代表切词后的词语，矩阵的元素为词语在文档中出现的频次。

from sklearn.feature_extraction.text import CountVectorizer

# 计算每个词在各评论内容中的次数，并将稀疏度为99%以上的词删除
counts = CountVectorizer(min_df = 0.001) #作用是留下来的词语所对应的文档数目必须在所有文档中至少占有1%的比例，去除过于稀疏的词语。

# 文档词条矩阵
dtm_counts = counts.fit_transform(words).toarray()

# 获取矩阵的列名称【其实这里的作用是获取所有的特征名，因为这时候已经有许多的特征了因为经过了切词】
columns = counts.get_feature_names()

# 将矩阵转换为数据框--即X变量
X = pd.DataFrame(dtm_counts, columns=columns)

# 情感标签变量
y = evaluation.Type
#X.head()

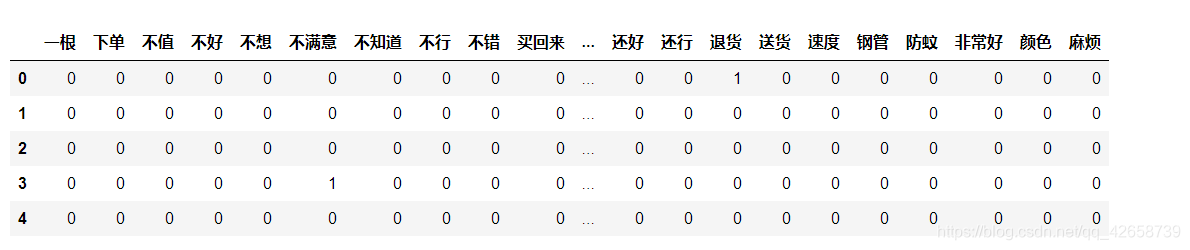
拆分数据并建模训练：

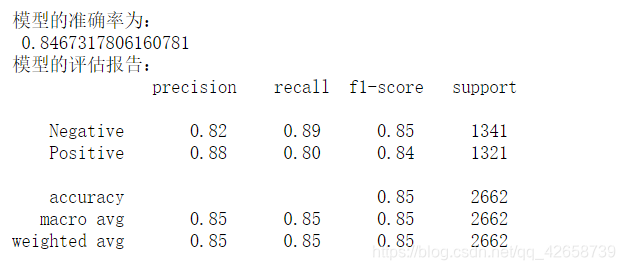
# 将数据集拆分为训练集和测试集
X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size = 0.25, random_state=1)

# 构建伯努利贝叶斯分类器
bnb = naive_bayes.BernoulliNB()

# 模型在训练数据集上的拟合
bnb.fit(X_train,y_train)

# 模型在测试数据集上的预测
bnb_pred = bnb.predict(X_test)
# 模型的预测准确率
print('模型的准确率为：
',metrics.accuracy_score(y_test, bnb_pred))
print('模型的评估报告：
',metrics.classification_report(y_test, bnb_pred))

希望大家能给予意见和建议。谢谢！