【洛谷】普及区_树形数据结构（不全）

简单说说二叉树。

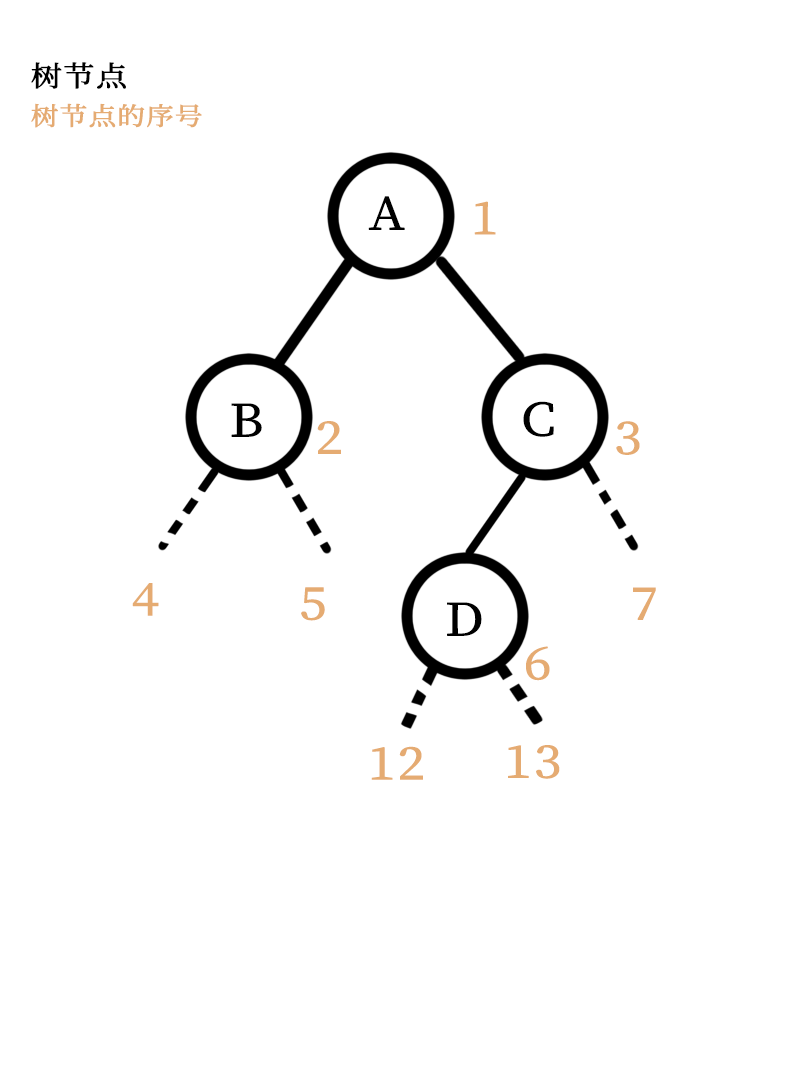
如图：

二叉树的每个树节点都有两个子节点（通俗称作父子关系）；

节点A，他是B和C两个节点的爸爸，D节点可以说是他的孙子；

节点B，没有儿子；

节点C，只有一个左儿子D；

节点D，没有儿子。

聪明的你肯定发现：

左儿子的序号等于父亲序号的2倍，右儿子的序号等于父亲序号的2倍+1；

因此可以利用递归遍历整棵二叉树。

P1087 FBI树

本题对于二叉树新人来说难点是建树（比如我在课间想了一上午才明白）。

（其实只要动动笔在纸上画一画就很清楚了）

其次就是查询字符串的“FBI”值（弄一个判断函数）

#include<cstdio>
#include<iostream>
#include<string>
using namespace std;

int N, count;
string s;
char FBI[10000];

char find(string s){ // 查询
    int h = 0;
    bool one = true;
    for(int i = 0; i < s.size(); i++){
        if(h == 1 && s[i] == '0') one = false;
        if(h == -1 && s[i] == '1') one = false;
        if(s[i] == '1' && i == 0) h = 1;
        if(s[i] == '0' && i == 0) h = -1;
    }
    if(one){
        if(h == 1) return 'I';
        else return 'B';
    }
    else return 'F';
}

void solve(string s){ // 建树
    if(s.size() == 1){
        FBI[count++] = find(s);
        return ;
    }
    string a = s.substr(0, s.size()/2), b = s.substr(s.size()/2);
    solve(a); // 左儿子
    solve(b); // 右儿子
    FBI[count++] = find(s);
    return ;
}

int main(){
    while(cin >> N){
        cin >> s;
        count = 0;
        solve(s);
//        printf("count:%d
", count);
        for(int i = 0; i < count; i++) cout << FBI[i];
        cout << endl;
    }
    return 0;
}

string的substr对于复制string屡试不爽，推荐一下。

下一题：

P1030 求先序排列

前中后序排列指的是二叉树怎么查询的问题。

推荐博客：看懂二叉树的三种遍历（比较容易理解）

（前序排列：根左右； 中序排序：左根右；后序排序：左右根；）

题目样例：

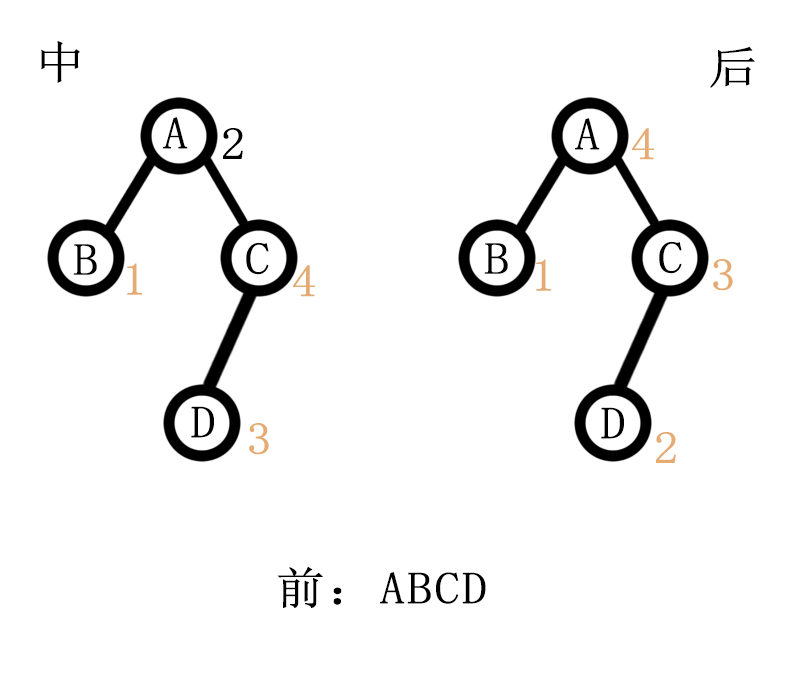
手写一下，会发现：

后序排列的末位肯定是前面所有节点的父节点；

然后在中序排列里找到那个父节点就可以把字符串分成两部分；

中：BADC　→　中：B    DC　→　中：B　　D

后：BDCA　→　后：B    CD　→　后：B　　D

查找的同时把父节点（后序排列字符串的末尾）输出。

（题目样例过于简单，可在上述的博客研究更复炸的树）

#include<iostream>
#include<string>
using namespace std;

string a, b; // a是中序， b是后序

void solve(string a, string b){
    if(b.size() > 0){
        cout << b[b.size()-1];
        int n = a.find(b[b.size()-1]);
        solve(a.substr(0, n), b.substr(0, n));
        solve(a.substr(n+1), b.substr(n, a.size()-n-1));
    }
    return ;
}

int main()
{
    while(cin >> a >> b){
        solve(a, b);
        cout << endl;
    }
    return 0;
}

（参考了洛谷第一位题解，自己弄了一晚上把自己弄晕了@-@）

下一题：

P1305 新二叉树

经过上两题的练习后，相信看到这里的你对于这题的第一感觉就可以用暴力建树解决了（没错，我就是这么解决的）

后面n行的第一个字目表示父节点——找到父节点的序号，左右儿子就简单储存（暴力遍历）

最后搜索一下就AC了。

（一开始数据建少了，所以会RE与WA。要注意的是，父节点的序号是从1开始的，如果从0开始，0*2还是等于0的quq）

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int N, par;
char s[5005];
char t[3];

void print(char s[], int i){
    if(s[i] == '*') return ;
    cout << s[i];
    print(s, i*2);
    print(s, i*2+1);

    return ;
}
int main()
{
    cin >> N;
    for(int i = 0; i < 5000; i++) s[i] = '*';
    for(int i = 0; i < N; i++){
        cin >> t;
        if(i == 0) s[1] = t[0];

        for(int f = 1; f < 5000; f++){
            if(s[f] == t[0]) {
                par = f;
                break;
            }
        }
        s[par*2] = t[1];
        s[par*2+1] = t[2];
    }

    print(s, 1);
    cout << endl;

    return 0;
}