一、排序算法
常见的排序算法主要分为下面几类:
-
- 选择排序
- 堆排序
- 冒泡排序
- 快速排序
- 插入排序
- 希尔排序
- 归并排序
- 桶式排序
- 基数排序
本文主要介绍选择排序、堆排序、冒泡排序、快速排序和归并排序的原理和Java代码实现。
二、算法实现
2.1 选择排序
选择排序的原理:
选择排序是一种简单直观的排序算法,它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
Java实现:
public static void selSort(int a[]){
if(a==null||a.length==0){
return;
}
for (int i = 0; i < a.length; i++) {
int tmp = a[i];//存储遍历时最小的值
int flag = i;//存储最小值的位置
for(int j = i+1;j<a.length;j++){
if(a[j]<tmp){
//找到更小的值,将值和位置存储起来
tmp = a[j];
flag = j;
}
}
int tmp2 = a[i];//临时保存a[i]的值,用于交换值得位置
a[i] = tmp;
a[flag] = tmp2;
}
}
2.2 堆排序
堆排序的原理:
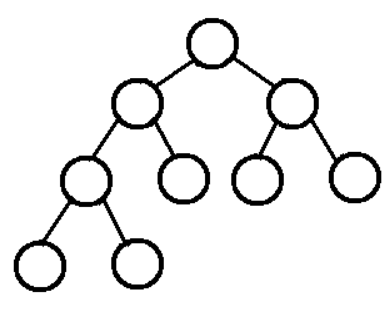
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序。堆是具有以下性质的完全二叉树:
- 每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;
- 每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
- 完全二叉树: 除了最后一层之外的其他每一层都被完全填充,并且所有结点都保持向左对齐。
它的基本思想是将待排序的序列构造成一个大顶堆(或小顶堆)。此时,整个序列的最大值就是堆顶的根节点,将其与堆数组的末尾元素交换,此时末尾元素就是最大值,然后将剩余的 n-1 个序列重新构造成一个最大堆,再将新的最大堆的顶与末尾元素交换,如此反复执行,便能得到一个有序序列了。
Java实现
public static void heapSort(int[] arr){
buildMaxHeap(arr);
int heapSize = arr.length;
//最大值的节点与最后一个节点交换位置
for (int i = arr.length - 1; i > 0; i--) {
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
//最后一个节点为最大值后,再对前边节点进行堆排序,每交换出一个最大值,最大堆的大小减1
heapSize--;
maxHeapify(arr, 0, heapSize);
}
}
/**
* 4 3 9 5 10 2 6
* 0 1 2 3 4 5 6
*
* 4
* 3 9
* 5 10 2 6
*
* @param arr 待排序的数组
* @param index 要进行调整的节点位置
* @param heapSize 最大堆的大小
*/
public static void maxHeapify(int[] arr, int index, int heapSize) {
int leftIndex = 2 * index + 1;//左节点
int rightIndex = 2 * index + 2;
int largeIndex;//临时存储三个节点中最大的节点
if (leftIndex < heapSize && arr[leftIndex] > arr[index]) {
largeIndex = leftIndex;
} else {
largeIndex = index;
}
if (rightIndex < heapSize && arr[rightIndex] > arr[largeIndex]) {
largeIndex = rightIndex;
}
if (largeIndex != index) {
//与最大值的节点交换位置
int temp = arr[largeIndex];
arr[largeIndex] = arr[index];
arr[index] = temp;
//递归的方式对新的节点进行最大堆调整
maxHeapify(arr, largeIndex, heapSize);
}
}
//建立最大堆,遍历其中的非叶子节点,调整位置,达到最大堆的特点,即父节点的值大于子节点的值
public static void buildMaxHeap(int[] arr) {
int heapSize = arr.length;
for (int i = (arr.length - 2) / 2; i > -1; i--) {
maxHeapify(arr, i, heapSize);
}
}
2.3 冒泡排序
冒泡排序的原理:
冒泡排序需要重复地走访要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,该数列就已经排序完成。
步骤如下所示:
-
-
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
-
Java实现
/**
* 冒泡排序
* 每次选择两个相邻的值进行比较,较小的放在前面
* 第一轮比较时,第一个和第二个比较,第二个和第三个比较,一直到最后一个
* 第一轮结束,最后一个值为最大值
* 再进行第二轮比较,比较时,无需再比较最后一个值
* ...
* 依次类推,保证每一轮的最后一个值都是最大值,直到没有值再与第一个值比较时,循环结束
* @param a
*/
public static void bubSort(int a[]){
for(int i=0; i<a.length; i++){
//第一轮比较完后,最后一个位置的值为最大值
//每遍历一轮,最后的位置就能多确定一个
for(int j=0; j<a.length-i-1; j++){
int tmp = a[j];//保存a[j]的值,如果比下一个值大,则交换位置
if(a[j]>a[j+1]){
a[j] = a[j+1];
a[j+1] = tmp;
}
}
}
}
2.4 快速排序
快速排序的原理:
快速排序采用了分治的思想,将一个数组分成多个子数组,当子数组满足排序时,整个数组则已经排好序。它的基本思想是通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
Java实现
/**
* 快速排序
* 选择一个基准值,将比其小的值放在左边,比其大的值放在右边
* 对新产生的数组左边和右边再递归以上动作
* 直到所有子数组都已排好序
* @param array 数组
* @param start 开始节点
* @param end 最后节点
*/
public static void quiSort(int[] array, int start, int end) {
if (start < end) {
//递归遍历
int position = partition(array, start, end);
quiSort(array, start, position - 1);
quiSort(array, position + 1, end);
}
}
public static int partition(int[] array, int start, int end) {
int position = start - 1;//开始时start前一个位置
int base = array[end];//选择最后一个元素为基准
for (int i = start; i < end; i++) {
//从开始节点遍历
if (array[i] <= base) {
position++;
//第i个元素和position位置元素交换位置
int temp = array[position];
array[position] = array[i];
array[i] = temp;
}
}
//最后一个元素与position交换位置
int temp = array[position + 1];
array[position + 1] = array[end];
array[end] = temp;
//返回基准所在的位置
return position + 1;
}
2.5 归并排序
归并排序的原理:
归并排序利用的是分治的思想实现的,对于给定的一组数据,利用递归与分治技术将数据序列划分成为越来越小的子序列,之后对子序列排序,最后再用递归方法将排好序的子序列合并成为有序序列。合并两个子序列时,需要申请两个子序列加起来长度的内存,临时存储新的生成序列,再将新生成的序列赋值到原数组相应的位置。
Java实现
public static void merSort(int[] arr,int left,int right){
if(left<right){
int mid = (left+right)/2;
merSort(arr,left,mid);//左边归并排序,使得左子序列有序
merSort(arr,mid+1,right);//右边归并排序,使得右子序列有序
merge(arr,left,mid,right);//合并两个子序列
}
}
private static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[right - left + 1];//ps:也可以从开始就申请一个与原数组大小相同的数组,因为重复new数组会频繁申请内存
int i = left;
int j = mid+1;
int k = 0;
while(i<=mid&&j<=right){
if (arr[i] < arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while(i<=mid){//将左边剩余元素填充进temp中
temp[k++] = arr[i++];
}
while(j<=right){//将右序列剩余元素填充进temp中
temp[k++] = arr[j++];
}
//将temp中的元素全部拷贝到原数组中
for (int k2 = 0; k2 < temp.length; k2++) {
arr[k2 + left] = temp[k2];
}
}