C#实现约瑟夫环数学问题

描述

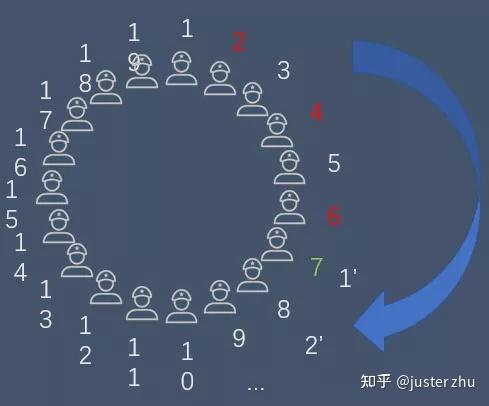
据说在罗马帝国时期，犹太士兵被罗马人包围。犹太士兵为了不被俘虏决定集体自sha，自sha的方式是所有人围成一个圆。

 

 

思路如下：

• 第一个士兵会kill掉他左边第二个士兵
• 第三个士兵会kill掉第四个士兵
• 第五个士兵kill掉第六个士兵
• 以此类推...直到最后剩下一人再自sha。

犹太士兵里有个人叫约瑟夫，他想投降保命但又不能明说。那么约瑟夫应该站在哪个位置上才能成为最后一个剩下的人？这样就不用自sha可以直接向罗马人投降。在人数不多的情况下这个问题很好推算，假设总人数10人的前置条件。

 

 

思路如下：

第一轮

• 1 kill 2
• 3 kill 4
• 5 kill 6
• 7 kill 8
• 9 kill 10

第二轮

• 1 kill 3
• 5 kill 7
• 9 kill 1
• 5 kill 9

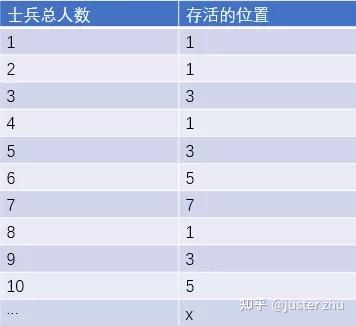
最终活下来的是5号位，但是士兵有100人、1000人呢？约瑟夫没有那么多时间进行推算。把总人数和最终存活的位置整理成图表的话大致如下：

 

 

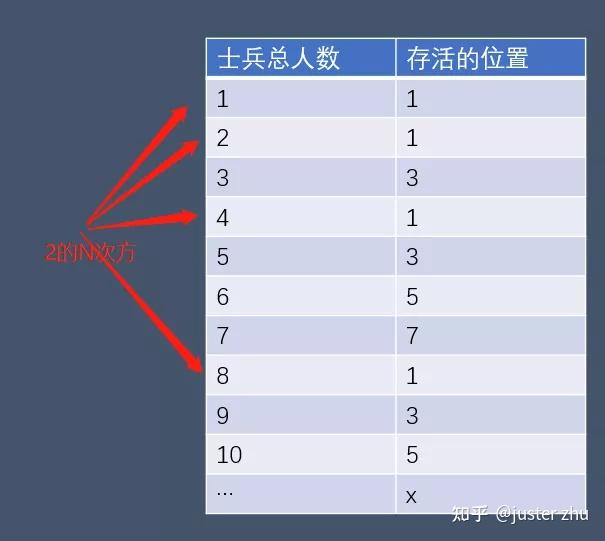
最终我们发现，活下来的都是奇数位。因为最先杀人的士兵都处在奇数位置，不管人数多少最先被kill掉的肯定是站在偶数位置上的人。也就是约瑟夫绝对不能站在偶数位置上。第二点我们在图表中多次发现存活位置1，也就是士兵1最后会存活的情况的总人数些情况恰好是2的N次方。

 

 

我们来分析一下规律，假设士兵总人数是8个也就是2的3次方，

• 第一轮kill完，偶数位置上的人都挂了
• 第二轮重新标记位置，还是士兵1号位先动手仍然是偶数位上的人都挂了，剩下的就是1号士兵。

按照这个逻辑如果士兵总人数是2的N次方的情况下最后存活的一定是士兵1。

 

如果人数是19不是2的N次方怎么办？

 

 

如果人数是19不是2的N次方但仍可以把19写成3+2的4次方。可以理解成先排除掉这多余的三个人，然后重新编号再从1'开始在进行一轮搏杀最终剩下的就是1'这个1'就是原来的士兵7。

 

 

 

C#代码

/// <summary>
    /// 约瑟夫一下
    /// </summary>
    /// <param name="num">总人数</param>
    /// <returns>可存活下来的位置</returns>
    int Joseph(int num)
    {
        for (int i = 31; i >= 0; i--)
        {
            if (((num >> i) & 1) == 1)
            {
                num ^= 1 << i;
                return num * 2 + 1;
            }
        }
        return 0;
    }

结尾

有机智的小伙伴会问了，人数是2的n次方下1号位能活下来那大家都会抢着当1号位。那么如何保证拿到1号位呢？

答：先动手的那个。（doge