[TopCoder - 12244 SRM 559 Round1 Div1] CircusTents
小而精的计算几何题
题目大意:有(n)个实心圆(不能从内部经过)
在第一个圆上选出一个点,使得从其他任意圆上到达它的最小距离 最大
分析:要最小值最大,显然可以想到二分答案
不能穿过其他圆这一条件让计算答案变得十分困难,但是可以发现,如果路径经过了一号圆以外的圆
那么从路径与该圆的交点直接过去的距离一定更近
也就是说,可以把 距离 看做 可以穿过一号圆以外的圆 的距离
考虑从一个圆(O)到达一号圆上的某一点(X)的最小距离,大致可以成两种情况
1.(OX)连线不穿过一号圆,那么可以直接走(OX)连线
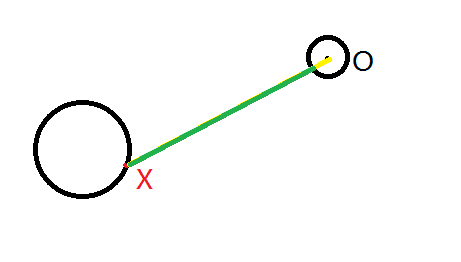
最优路径就是绿色线
2.先走一条切线,然后绕着圆周走一段
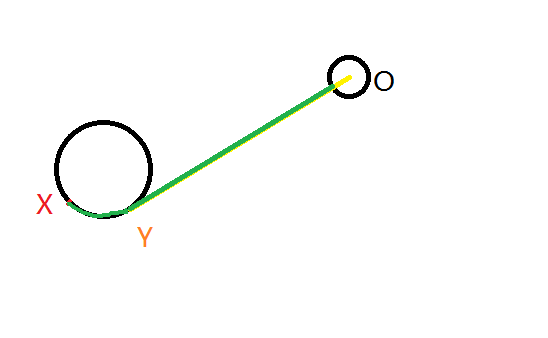
其中(Y)是(O)点对于一号圆的切线的切点,绿色线+圆弧是最优路径
那么二分答案(mid)之后,可以发现满足距离(ge mid)的选点位置是一段圆弧,可以从角度取交集判断是否有解
实现上,可以先把一号圆平移到远点
然后对于其他的圆,按照角度范围是否在切线内部可以分类讨论
#include<bits/stdc++.h>
using namespace std;
typedef double db;
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(int i=a,i##end=b;i>=i##end;--i)
template <class T> inline void cmin(T &a,const T &b){ ((a>b)&&(a=b)); }
template <class T> inline void cmax(T &a,const T &b){ ((a<b)&&(a=b)); }
const int N=110;
const db eps=1e-10,Pi=acos(-1),D=2*Pi;
int n;
struct Cir{
int x,y,r;
}A[N];
db X[N],Y[N],H[N];
int C,S[N];
db Norm(db x){ return x<0?x+D:x; }
int I(db x){ return lower_bound(H+1,H+C+1,x)-H; }
int Check(db L){
memset(S,0,sizeof S);
H[1]=0,H[C=2]=D;
rep(i,1,n) {
db dis=A[i].x*A[i].x+A[i].y*A[i].y;
db t=sqrt(dis-A[0].r*A[0].r)-A[i].r;
//t为走过切线的距离
dis=sqrt(dis);
if(dis-A[0].r-A[i].r>=L){ X[i]=0,Y[i]=D; continue; }
db l,r;
if(t>=L) {
// 说明范围在切线位置以内
// 此时,满足d=dis((x0,y0),A[i].O)-A[i].r>=L
db a=dis,b=A[0].r,c=L+A[i].r;
db co=(a*a+b*b-c*c)/(2*a*b);
//余弦定理
db x=acos(co),y=atan2(A[i].y,A[i].x);
l=y+x,r=y-x+D;
} else {
db d=acos(A[0].r/dis);
db x=atan2(A[i].y,A[i].x);
db y=(L-t)/A[0].r+d;
// 圆弧长度/半径得到圆弧弧度
if(y>Pi) return 0; // 特判一下全部覆盖的情况
l=x+y,r=x-y+D;
}
// 求 [l,r] 的交
if(r>D) l-=D,r-=D;
if(r<=0) l+=D,r+=D;
H[++C]=Norm(X[i]=l),H[++C]=Y[i]=r;
}
sort(H+1,H+C+1);
rep(i,1,n) {
if(X[i]>=0) S[I(X[i])]++,S[I(Y[i])]--;
else S[I(0)]++,S[I(Y[i])]--,S[I(X[i]+D)]++,S[I(D)]--;
}
// 暴力求交
rep(i,1,C) if((S[i]+=S[i-1])==n) return 1;
return 0;
}
class CircusTents {
public:
double findMaximumDistance(vector <int> _x, vector <int> _y, vector <int> _r) {
n=_x.size()-1;
rep(i,0,n) A[i]=(Cir){_x[i]-_x[0],_y[i]-_y[0],_r[i]};
db l=0,r=1e5;
while(r-l>eps) {
db mid=(l+r)/2;
if(Check(mid)) l=mid;
else r=mid;
}
return l;
}
};