

期望:100 实际:100

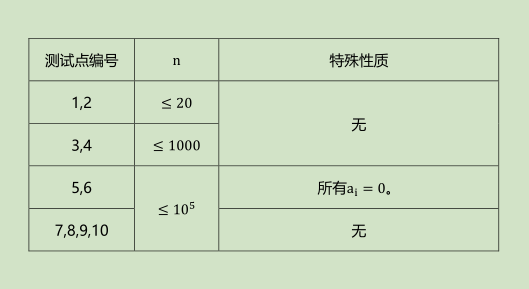
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define MAXN 100010 using namespace std; int n,s,num; int a[MAXN]; long long ans; int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int cmp(int x,int y){ return x>y; } int main(){ freopen("median.in","r",stdin); freopen("median.out","w",stdout); n=read();s=read(); for(int i=1;i<=n;i++) a[i]=read(); sort(a+1,a+1+n,cmp); int mid=n/2; for(int i=1;i<=n;i++) if(a[i]>=s) num++; else{ if(num<=mid){ ans+=(s-a[i]);num++; } else if(num>mid) break; } cout<<ans; }

期望:20~40 实际:0

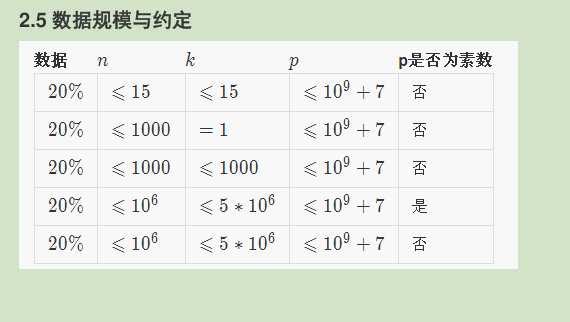
/* 思路:感觉可以用卡特兰数搞一下。 应该可以推出递推式。 */ #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n,p,k; long long ans; int vis[10010]; int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } void dfs(int now,int num1,int num2){ if(num1>n) return ; if(num1+(2*n-now)+1<n) return ; if(num2-num1>=k) return ; if(now==2*n+1){ if(num1==n){ ans+=1; ans%=p; } return ; } vis[now]=1;dfs(now+1,num1+1,num2);vis[now]=0; dfs(now+1,num1,num2+1); } int main(){ freopen("term.in","r",stdin); freopen("term.out","w",stdout); n=read();k=read();p=read(); if(n<=15){ dfs(1,0,0); printf("%d ",ans); } else if(k==1){ ans=1; for(int i=2*n;i>=n+2;i--){ int j=2,num=i; while(j<=n){ if(!vis[j]){ if(num%j==0){ num/=j; vis[j]=1; } } j++; } ans=ans*num; } for(int i=2;i<=n;i++) if(!vis[i]) ans/=i; cout<<ans%p; } }

看出是卡特兰数了,但是对于非质数的除法取莫出现了问题

#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n,k,p,tot; int prime[10000],num[100000]; int vis[10010],mn[100010],yes[100010]; int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } void pre(){ memset(yes,true,sizeof(yes)); yes[1]=false; for(int i=2;i<=2*n;i++){ if(yes[i]) prime[++tot]=i,mn[i]=tot; for(int j=1;i*prime[j]<=n;j++){ yes[i*prime[j]]=false; if(i%prime[j]==0) break; } } } void insert(int x,int opt){ while(x!=1){ num[mn[x]]+=opt; x=x/prime[mn[x]]; } } int fastpow(long long a,long long b){ long long s=1; for(;b;b>>=1){ if(b&1) s=a*a%p; a=a*a%p; } return s; } int findans(){ long long ans=1; for(int i=1;i<=tot;i++) if(num[i]) ans=(1ll*ans*fastpow(prime[i],num[i]))%p; return ans; } int main(){ // freopen("term.in","r",stdin); //freopen("term.out","w",stdout); n=read();k=read();p=read(); pre(); for(int i=n+1;i<=2*n;i++) insert(i,1); for(int i=1;i<=n;i++) insert(i,-1); long long ans1=findans(); memset(num,0,sizeof(num)); for(int i=n+k+1;i<=2*n;i++) insert(i,1); for(int i=1;i<=n-k;i++) insert(i,-1); long long ans2=findans(); cout<<(ans1-ans2+p)%p; }

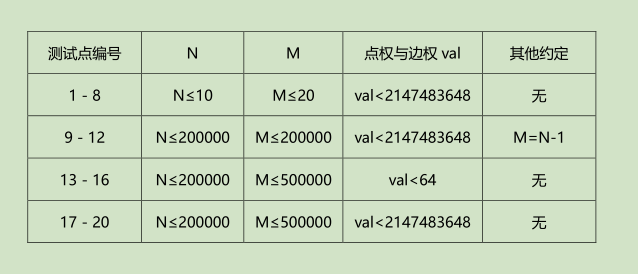
发现正反跑spfa有70分。

#include<map> #include<queue> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define MAXN 500010 using namespace std; map<int,bool>ma[MAXN]; int tim,top,sumcol; int n,m,s,t,tot,tot1,tot2; struct nond{ int id,dis; }; int low[MAXN],dfn[MAXN],col[MAXN]; int val[MAXN],val1[MAXN],di[MAXN],dis[MAXN]; int stack[MAXN],vis[MAXN],visstack[MAXN]; int to[MAXN],cap[MAXN],net[MAXN],head[MAXN]; int to1[MAXN],cap1[MAXN],net1[MAXN],head1[MAXN]; int to2[MAXN],cap2[MAXN],net2[MAXN],head2[MAXN]; int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } void add(int u,int v,int w){ to[++tot]=v;cap[tot]=w;net[tot]=head[u];head[u]=tot; } void add2(int u,int v,int w){ to1[++tot1]=v;cap1[tot1]=w;net1[tot1]=head1[u];head1[u]=tot1; } void add3(int u,int v,int w){ to2[++tot2]=v;cap2[tot2]=w;net2[tot2]=head2[u];head2[u]=tot2; } void tarjin(int now){ low[now]=dfn[now]=++tim; stack[++top]=now; vis[now]=1;visstack[now]=1; for(int i=head[now];i;i=net[i]) if(visstack[to[i]]) low[now]=min(low[now],dfn[to[i]]); else if(!vis[to[i]]){ tarjin(to[i]); low[now]=min(low[now],low[to[i]]); } if(dfn[now]==low[now]){ sumcol++; col[now]=sumcol; while(stack[top]!=now){ col[stack[top]]=sumcol; visstack[stack[top]]=0; top--; } visstack[now]=0; top--; } } void spfa(int S){ queue<int>que; memset(vis,0,sizeof(vis)); memset(di,0x7f,sizeof(di)); vis[S]=1;di[S]=val1[S]; que.push(S); while(!que.empty()){ int now=que.front(); que.pop(); vis[now]=0; for(int i=head1[now];i;i=net1[i]) if(di[to1[i]]>=(di[now]&cap1[i]&val1[to1[i]])){ di[to1[i]]=(di[now]&cap1[i]&val1[to1[i]]); if(!vis[to1[i]]){ vis[to1[i]]=1; que.push(to1[i]); } } } } void spfa1(int S){ queue<int>que; memset(vis,0,sizeof(vis)); memset(dis,0x7f,sizeof(di)); vis[S]=1;dis[S]=val1[S]; que.push(S); while(!que.empty()){ int now=que.front(); que.pop(); vis[now]=0; for(int i=head2[now];i;i=net2[i]) if(dis[to2[i]]>=(dis[now]&cap2[i]&val1[to2[i]])){ dis[to2[i]]=(dis[now]&cap2[i]&val1[to2[i]]); if(!vis[to2[i]]){ vis[to2[i]]=1; que.push(to2[i]); } } } } int main(){ freopen("rabbit.in","r",stdin); freopen("rabbit.out","w",stdout); n=read();m=read();s=read();t=read(); for(int i=1;i<=n;i++) val[i]=read(); for(int i=1;i<=m;i++){ int u=read(); int v=read(); int w=read(); add(u,v,w); } for(int i=1;i<=n;i++) if(!vis[i]) tarjin(i); for(int i=1;i<=n;i++) for(int j=head[i];j;j=net[j]) if(col[i]!=col[to[j]]) if(ma[col[i]].find(col[to[j]])==ma[col[i]].end()){ ma[col[i]][col[to[j]]]=1; add2(col[i],col[to[j]],cap[j]); add3(col[to[j]],col[i],cap[j]); } memset(vis,0,sizeof(vis)); for(int i=1;i<=n;i++) if(!vis[col[i]]) val1[col[i]]=val[i],vis[col[i]]=1; else val1[col[i]]=(val1[col[i]]&val[i]); for(int i=1;i<=n;i++) for(int j=head[i];j;j=net[j]) if(col[i]==col[to[j]]) val1[col[i]]=(val1[col[i]]&cap[j]); spfa(col[s]); spfa1(col[t]); if(di[col[t]]==0x7f7f7f7f){ puts("-1");return 0; } else{ printf("%d ",min(di[col[t]],dis[col[s]]));return 0; } }

/* ————该题目主要考察tarjan缩点,拓扑排序和贪心 40pts: 直接爆搜,看每条边走不走,复杂度 ,此部分分贪心将所有权值&起来是有分的(给对题目做了一定分析的盆友的彩蛋) 60pts: 对于M = N - 1的点,其实他并不是树QWQ,因为题目中明确说了不保证联通,所以这个部分分是个假的。但是为了多给大家送点分,此部分数据采用随机生成,不论是用不正确的spfa还是dijkstra都能够跑过去,是不是很良心。 80pts: 考虑每个联通分量中,能走的肯定要尽量去走,然后我们缩点求出连通分量的贡献,转换成DAG上的问题,然后发现DAG上不能够简单地按照拓扑序取min做dp转移,但是我们可以对DAG上每一个位置开一个64的数字记录到这个节点各个数字是否可行,然后拓扑序转移,复杂度64(N + M) 还是能跑过去的 100pts: 既然每个二进制位上的数字互不干扰,我们就拆分二进制做。 考虑从高位向低位枚举二进制位,我们肯定是希望高位上能够为0,那么我们考虑在整个DAG中的那些路径是能够使这一位为0的,显然,在所有从s到t的道路中,若存在某个点或者边,那么他所有的后继路径和前驱路径都是可行的,那么我们可以正反拓扑两次找到所有可行的点边集合作为当前答案。 然后考虑下一位,下一位中因为要保证上一位是0,所以能够走的点和边肯定是上次得到的点边集合里的,我们在这个得到的集合中在尽行同样的拓扑看看当前位是否可行,如果可行的话就用新得到的点边集合去更新原图的点边集合。 如此做三十次考虑所有的为就能得到答案了。 */ #include<cstdio> #include<algorithm> #include<cstring> #include<queue> #include<iostream> #include<ctime> #include<cmath> #include<set> #include<map> #define ll long long #define M 700010 struct Edge { int vi, vj, v; } edge[M]; struct Note { int vj, v, id; } be; using namespace std; int read() { int nm = 0, f = 1; char c = getchar(); for(; !isdigit(c); c = getchar()) if(c == '-') f = -1; for(; isdigit(c); c = getchar()) nm = nm * 10 + c - '0'; return nm * f; } vector<int>to[M]; vector<Note> to1[M], to2[M]; int belong[M], st[M], dfn[M], low[M], dft, n, m, s, t, note[M], noww[M], tp, tot, sz[M], ans = 2147483647, rudu1[M], rudu2[M]; bool vis[M]; void tarjan(int now) { vis[now] = true; st[++tp] = now; dfn[now] = low[now] = ++dft; for(int i = 0; i < to[now].size(); i++) { int vj = to[now][i]; if(!dfn[vj]) { tarjan(vj); low[now] = min(low[now], low[vj]); } else if(vis[vj]) low[now] = min(low[now], dfn[vj]); } if(dfn[now] == low[now]) { tot++; while(st[tp] != now) { int x = st[tp]; vis[x] = false; noww[tot] &= note[x]; belong[x] = tot; tp--; } int x = st[tp]; vis[x] = false; noww[tot] &= note[x]; belong[x] = tot; tp--; } } bool can[M], tmp1[M], tmp2[M]; int note1[M], note2[M], tp1, tp2; void tuopu() { queue<int>q; q.push(belong[t]); while(!q.empty()) { int op = q.front(); q.pop(); for(int i = 0; i < to2[op].size(); i++) { int vj = to2[op][i].vj; rudu2[vj]++; if(!vis[vj]) q.push(vj), vis[vj] = true; } } while(!q.empty()) q.pop(); q.push(belong[s]); while(!q.empty()) { int op = q.front(); note1[++tp1] = op; q.pop(); for(int i = 0; i < to1[op].size(); i++) { int vj = to1[op][i].vj; rudu1[vj]--; if(rudu1[vj] == 0) q.push(vj); } } q.push(belong[t]); while(!q.empty()) { int op = q.front(); q.pop(); note2[++tp2] = op; for(int i = 0; i < to2[op].size(); i++) { int vj = to2[op][i].vj; rudu2[vj]--; if(rudu2[vj] == 0) q.push(vj); } } } void work(int x) { for(int i = 1; i <= tot; i++) tmp1[i] = tmp2[i] = false; if((noww[belong[s]] & x) == 0) tmp1[belong[s]] = true; for(int i = 1; i <= tp1; i++) { int op = note1[i]; for(int j = 0; j < to1[op].size(); j++) { be = to1[op][j]; if((tmp1[op] == true) || (can[be.id] && ((be.v & x) == 0))) { tmp1[be.vj] = true; tmp1[be.id] = true; } else if((noww[be.vj] & x) == 0 && (can[be.vj])) tmp1[be.vj] = true; } } if((noww[belong[t]] &x) == 0) tmp2[belong[t]] = true; for(int i = 1; i <= tp2; i++) { int op = note2[i]; for(int j = 0; j < to2[op].size(); j++) { be = to2[op][j]; if((tmp2[op] == true) || (can[be.id] && ((be.v & x) == 0))) { tmp2[be.vj] = true; tmp2[be.id] = true; } else if((noww[be.vj] & x) == 0 && (can[be.vj])) tmp2[be.vj] = true; } } for(int i = 1; i <= tot; i++) tmp1[i] = (tmp1[i] | tmp2[i]); if(tmp1[belong[s]] && tmp1[belong[t]]) ans -= x; else return; for(int i = 1; i <= tot; i++) can[i] = (can[i] & tmp1[i]); } int main() { freopen("rabbit.in", "r", stdin); freopen("rabbit.out", "w", stdout); cin >> n >> m >> s >> t; for(int i = 1; i <= n; i++) note[i] = read(), noww[i] = 2147483647; for(int i = 1; i <= m; i++) { int vi = read(), vj = read(), v = read(); edge[i].vi = vi, edge[i].vj = vj, edge[i].v = v; to[vi].push_back(vj); } tarjan(s); if(!dfn[t]) { puts("-1"); return 0; } for(int i = 1; i <= m; i++) { int vi = edge[i].vi, vj = edge[i].vj, v = edge[i].v; vi = belong[vi], vj = belong[vj]; if(vi == 0 || vj == 0) continue; if(vi == vj) noww[vi] &= v; else { be.id = ++tot; be.vj = vj; be.v = v; to1[vi].push_back(be); rudu1[vj]++; be.vj = vi; to2[vj].push_back(be); } } if(belong[s] == belong[t]) { cout << noww[belong[s]] << " "; return 0; } tuopu(); for(int i = 1; i <= tot; i++) can[i] = true; for(int i = 30; i >= 0; i--) work(1 << i); cout << ans << " "; return 0; }
