常见的GAN网络的相关原理及推导
在上一篇中我们给大家介绍了GAN的相关原理和推导,GAN是VAE的后一半,再加上一个鉴别网络。这样而导致了完全不同的训练方式。
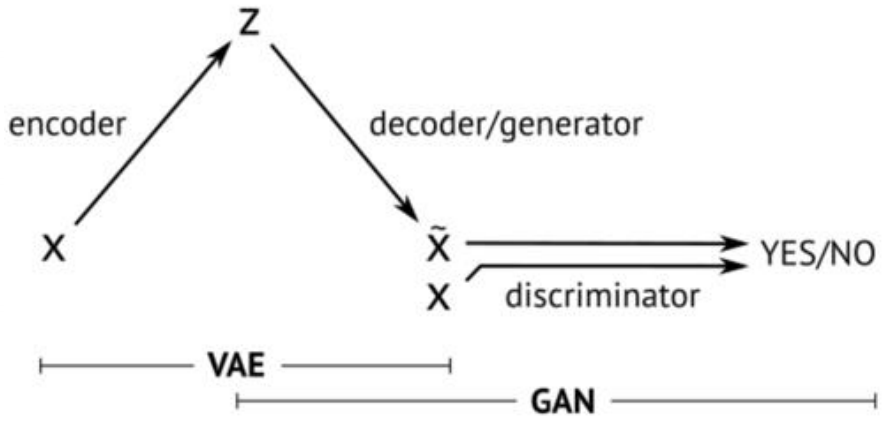
GAN,生成对抗网络,主要有两部分构成:生成器,判别器。
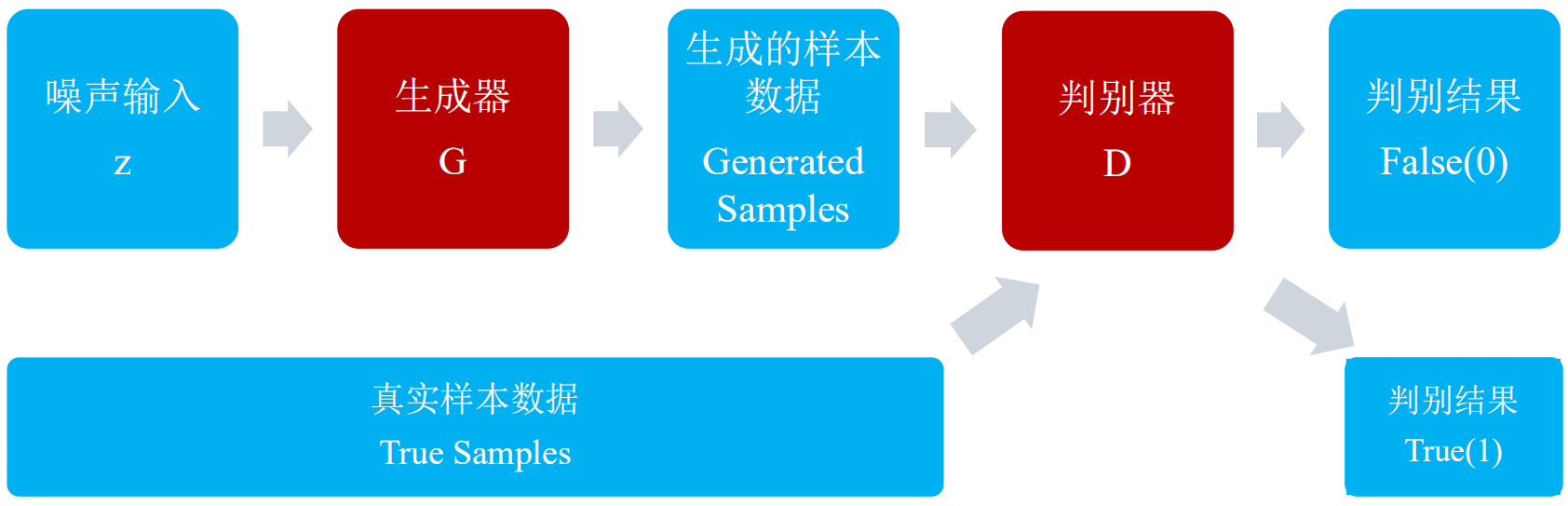
生成器网络的主要工作是负责生成样本数据,输入的是高斯白噪声z,输出的是样本数据向量x:
![]()
判别器网络的主要工作是负责检测样本的数据增加,输入真实或者生成的样本数据,输出样本的标签:
![]()
由于生成器和判别器都是需要经过网络进行训练的,所以两者都要能够微分。
生成对抗网络的工作方式是让第一代的G产生一些图片,然后把这些图片和一些真实的图片丢到第一代的D里面去学习,让第一代的D能够分别生成的图像和真实的图片。在训练第二代的G,第二代的G产生的图片,能够骗过第一代的D,在训练第二代的D,依次迭代。
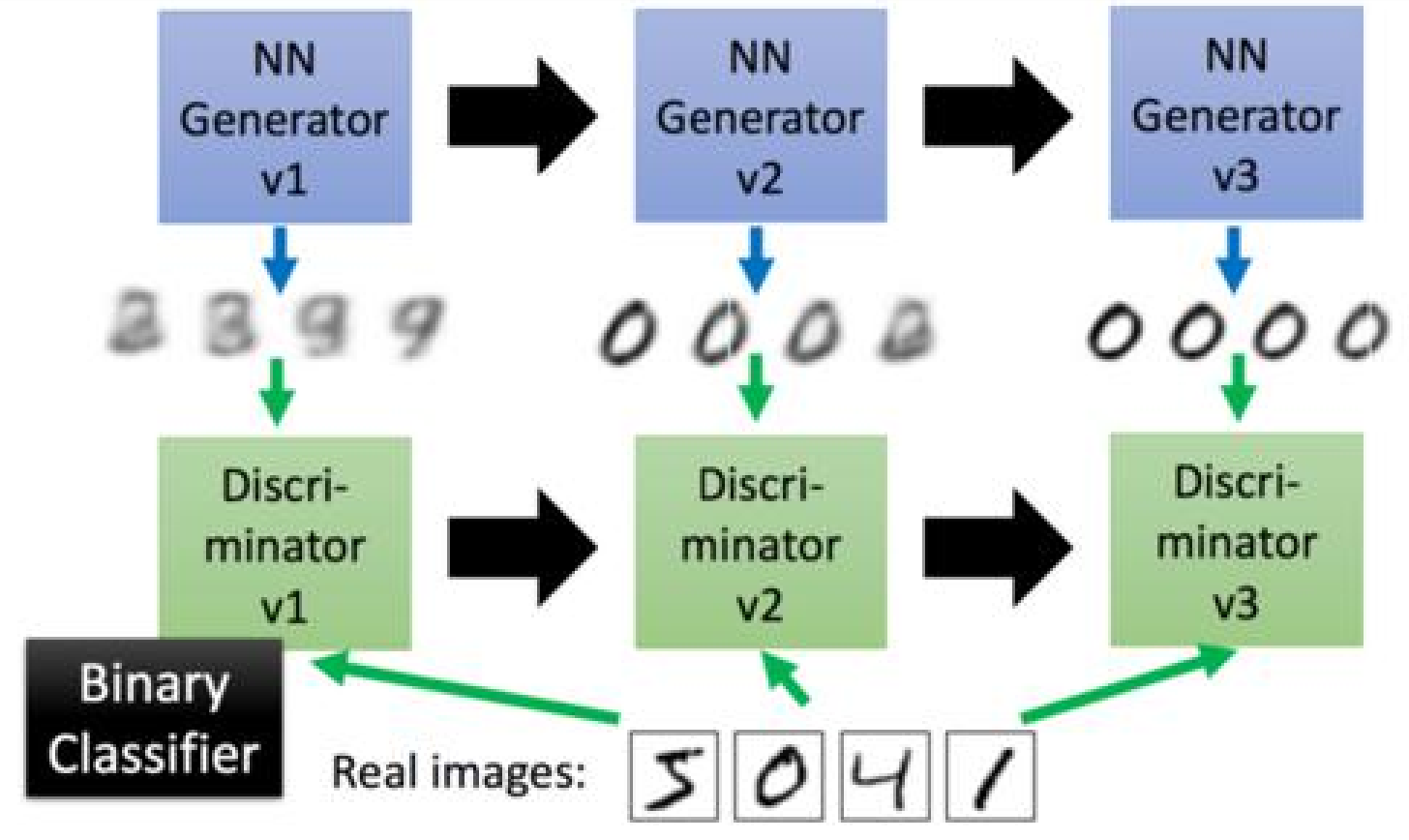
那么,问题就来了,如何训练新一代的G来骗过上一代的D呢?
我们可以把新一代的G和上一代的D连起来形成一个新的NN,我们训练最终的输出接近1,然后我们那中间的结果当做我们新的图片的输出。
优化函数
![]()
生成器G固定之后,使用![]() 来评价Pdata和Pz之间的差异。优化方式,对于生成器优化而言,我们要最小化价值函数,对于判别器而言,我们要优化最大价值函数,不断的交替进行之后,能够达到有个平衡点,称之为纳什均衡点。
来评价Pdata和Pz之间的差异。优化方式,对于生成器优化而言,我们要最小化价值函数,对于判别器而言,我们要优化最大价值函数,不断的交替进行之后,能够达到有个平衡点,称之为纳什均衡点。
![]()
![]()
生成器最小化目标即为判别器将生成数据识别为假的概率的log值,对于上述提到的均衡点,它是判别代价函数的鞍点。
对于GAN的训练算法,步骤如下:
a、执行D-step的minibatch优化k次:
1.从先验分布p(z)随机生成m个随机噪声向量z
2.从数据集分布p(x)里随机获取m个样本x
3.使用随机梯度上升优化判别器的代价函数
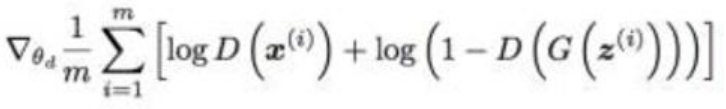
b.执行G-step的minibatch优化1次:
1.从先验分布p(z)随机生成m个随机噪声向量z
2.使用梯度下降优化生成器的代价函数
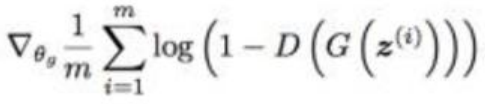
我们可以通过下面的曲线进一步理解训练过程:
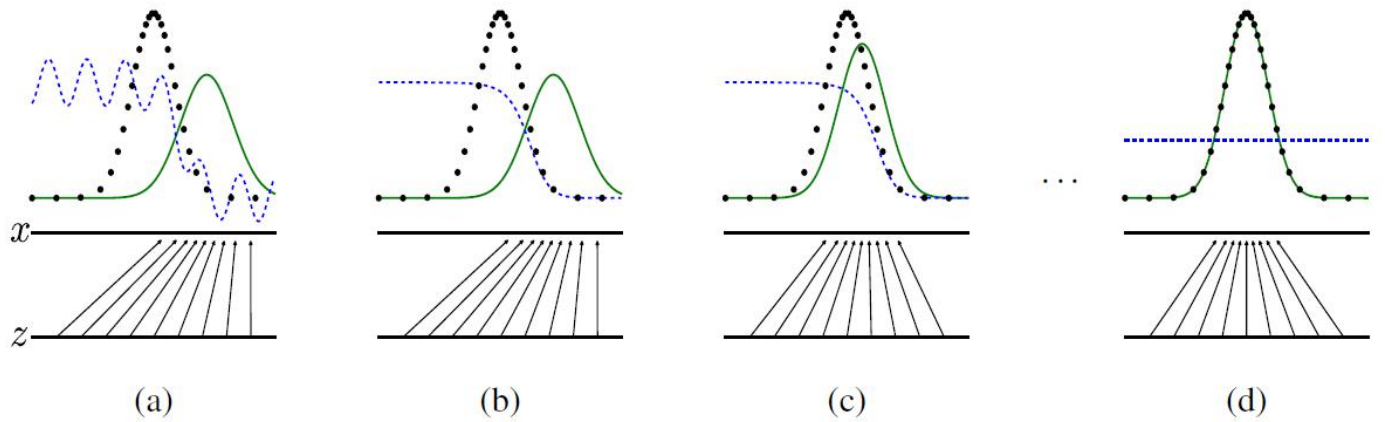
其中,绿线为生成器的数据分布,黑线为真实数据的分布,蓝线为判别器的结果分布。
GAN的问题:
GAN的训练比较困难,主要存在收敛难,很难达到纳什均衡点,并且无法有效监控收敛状态,另一方面,模型容易崩溃,判别器快速达到最优,能力明显强于生成器,生成器将数据集中生成在判别器最认可的空间上,即输出多样性低,不使用于离散输出(不可微分)。