A1103 Integer Factorization (30 分)

这道题我是根据晴神 DFS() 这一节给出的两个例子归纳的模板 AC 的，但实际上剪枝还不够完美 :-(

先说晴神 DFS 小节第一个例子：

有 n 件物品，每件物品的重量为 w[i]，价值为 c[i]。现在需要选出若干件物品放入一个容量为 V 的背包中，使得在选入背包的物品重量和不超过容量 V 的前提下，让背包中物品的价值之和最大，求最大价值。(1≤n≤20)

晴神给出的代码如下：

void DFS(int index, int sumW, int sumC) {
    //死胡同
    if (index == n) {
        return;//已经完成对 n 件物品的选择
    }

    //岔道口
    DFS(index + 1, sumW, sumC);//不选第 index 件物品
    if (sumW + w[index] <= V) {//只有加入第 index 件物品后未超过容量 V，才能继续
        if (sumC + c[index] > ans) {
            ans = sumC + c[index];//更新最大价值 maxValue
        }
        DFS(index + 1, sumW + w[index], sumC + c[index]);//选第 index 件物品
    }
}

根据这个算法我粗略地模拟了一下程序执行过程：

发现 DFS() 特点就是 1) 遍历所有子序列；2) 每个子序列都遍历到底，然后稍微总结了一下模板

/* 模板大概如下 */
void DFS(当前元素, 其他条件的数据..) {
    //死胡同
    if (当前为第 n 个元素)    return;

    //岔道口
    DFS(不选当前元素);
    if (剪枝条件)    DFS(选当前元素);
}

本来想尝试用这个模板做一下晴神 DFS 小节第二个例子，但是这个例子有点不同，先看例子：

给定 N 个整数（可能有负数），从中选择 K 个数，使得这 K 个数之和恰好等于一个给定的整数 X；如果有多种方案，选择它们中元素平方和最大的一个。数据保证这样的方案唯一。例如，从 4 个整数 {2, 3, 3, 4} 中选择 2 个数，使它们的和为 6，显然有两种方案 {2, 4} 和 {3, 3}，其中平方和最大的方案为 {2, 4}。

同样晴神给出了代码：

void DFS(int index, int nowK, int sum, int sumSqu) {
    if (nowK == k && sum == x) {//找到 k 个数的和为 X
        if (sumSqu > maxSumSqu) {//如果比当前找到的更优
            maxSumSqu = sumSqu;//更新最大平方和
            ans = temp;//更新最优方案
        }
        return;
    }
    //已经处理完 n 个数，或者超过 k 个数，或者和超过 x，返回
    if (index == n || nowK > k || sum > x)    return;

    //选 index 号数
    temp.push_back(A[index]);
    DFS(index + 1, nowK + 1, sum + A[index], sumSqu + A[index] * A[index]);
    temp.pop_back();
    //不选 index 号数
    DFS(index + 1, nowK, sum, sumSqu);
}

同样我也粗略模拟了一下

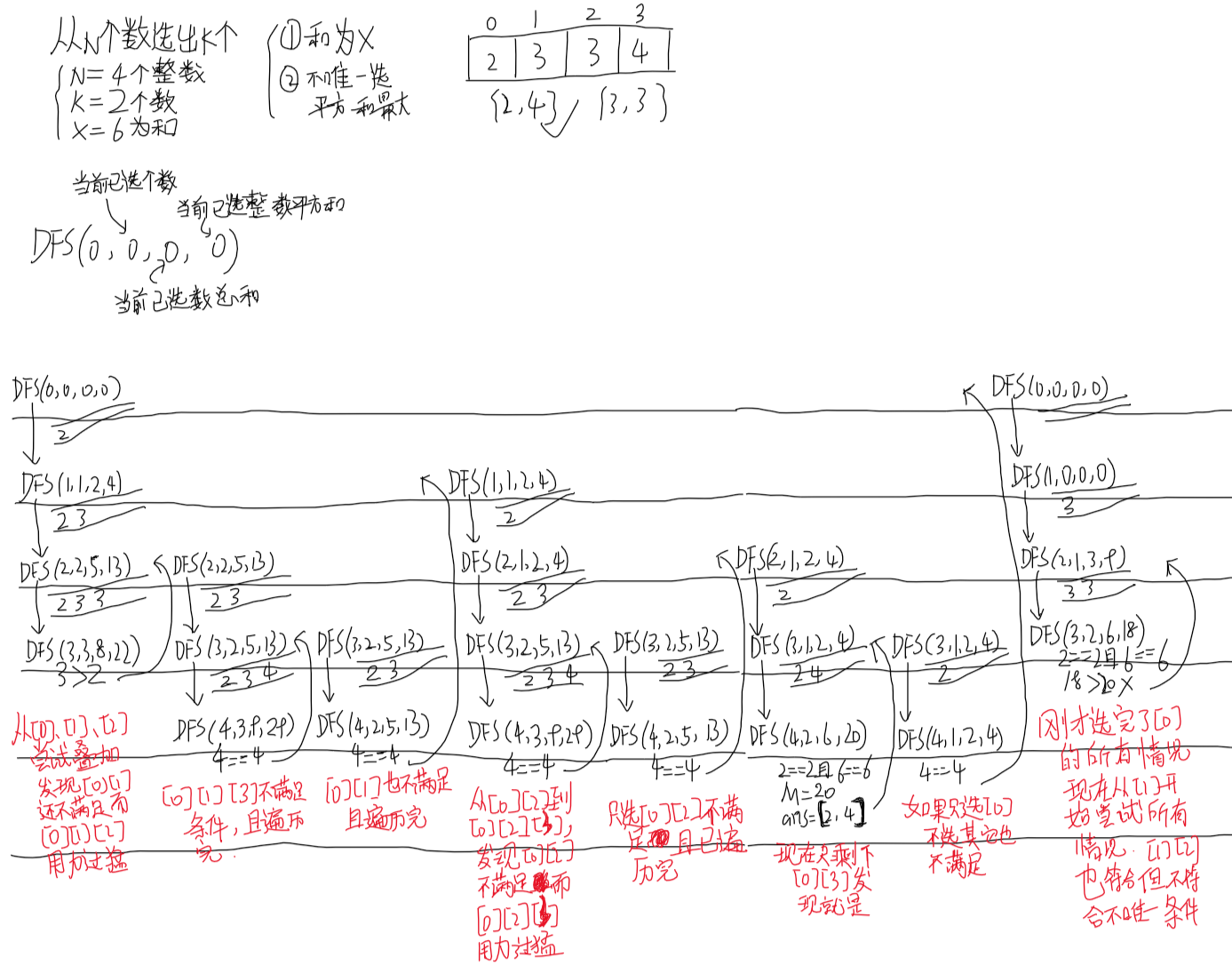
相比上一个例子，这个例子就多了个 "结果不唯一"，这需要记录每次满足条件的结果。晴神这边处理方法是多增加了一个逻辑块，让符合条件的所有结果都进来，然后在这里根据不唯一的条件再筛选一次。至于如何保存之前尝试的选择，晴神就是在 "选这个元素" 的前面和后面加一个  .push_back() 和  .pop_back() ，然后在这个筛选不唯一结果的逻辑块中更新这些尝试

/* 然后我改了一下模板 */
void DFS(当前元素, 其他条件..) {
    if (满足条件) {
        if (不唯一条件)    {...}
        return;
    }
    if (死胡同)    return;

    //岔道口
    DFS(不选当前元素);
    if (剪枝条件)    DFS(选当前元素);
}

最后我用这个模板试了一下 A1103，思路如下：

/* 思路 */

题目要求：
1、找 K 个数
2、这 K 个数的 P 方和等于 N
3、不唯一时找因子和最大的

模板中需要填充的地方：
1、形参中的 "其他条件" 就是题目的要求：
    K 个数：                 可以用 sumNum 记录选了几个数
    这 K 个数的 P 方和等于 N：可以用 sumPower 记录已选数的 P 方和
    不唯一时找因子和最大的：   可以用 sumFactor 记录已选数和
2、判断 1 的 "满足条件" 是指：
    (选了 K 个数) && (这 K 个数的 P 方和等于 N)
3、判断 1 里面的判断条件 "不唯一条件" 是指：
    因子和最大
4、"死胡同" 是指：
    (选完了所有元素) || (超过了 K 个数) || (K 个数的 P 方和大于 N)

最后确实能 AC，但我尝试了跑数据范围内最大的  400 399 2 非常非常非常非常久，我又试了试柳婼大神的代码：

 

:-( 

优化留着以后再看了，继续撸下一节 XD

点击获取完整代码