小数据池
1.什么是小数据池
小数据池就是python中一种提高效率的方式
小数据池支持:str,int,bool
ID就是查看空间的内存地址的
小数据池数字支持范围-5~256
2.小数据池启用的条件
代码块: 一个文件,一个模块,一个函数,一个类,终端中每一行都一个代码块
代码块在python中是用字典的方式去存储
电脑会先执行代码块,不符合的时候才会执行小数据池
is 和 == 的区别
- is 判断两个内存地址是否相同
- ==判断等号两边的值是否相同
- 如果==相同,is不一定相同
字符驻留机制
字符串驻留定义:在计算机科学中,字符串驻留一种仅保存一份相同且不可变字符串的方法。不同的值被存放在字符串驻留池中,即小数据池.
字符串驻留限制:仅包含下划线(_)、字母和数字的字符串会启用字符串驻留机制驻留。因为解释器仅对看起来像python标识符的字符串使用intern()方法,而python标识符正是由下划线、字母和数字组成。python只会针对整数范围为[-5, 256]的整数启用字符串驻留
字符串驻留机制的优缺点如下:
优点:能够提高一些字符串处理任务在时间和空间上的性能,
缺点:在创建或驻留字符串时的会花费更多的时间。
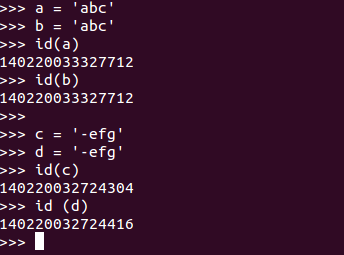
当字符串中没有特殊字符时(‘abc’),引用指向同一对象,即内存地址相同;
当字符串中有特殊字符时(‘-abc’),引用指向不同对象,即内存地址不同.
(字符串乘法)字符串会驻留的情况:
- 字符串做乘法的时候(与数字相乘)原字符串总长度不超过20()
- 自己定义的字符串,长度不限制,但字符串必须由字符/数字/下划线组成才能进行驻留
- 特殊字符(除中文外)定义1个时候,必须驻留
- 乘数为1的时候就是赋值,默认驻留
python3.7 乘法的时候总长度4096
怎么能自己驻留
需要使用python的内置模块
sys.intern() 指定驻留。
from sys import intern
a = intern("hello@")
b = intern("hello@")
print("intern 指定驻留:",b is a)
intern 指定驻留 : True
3.小数据池在哪里用?
面试的时候偶尔用到
解决自己的疑惑
集合
集合的形式:用大括号括起来,包含多个单独元素(不包含多个对象)
set {1,2,3}
s = {1,2,3}
- 存放的是单个元素
- 天然去重
- 集合是无序的
- 集合就是一个没有值的字典,遵循唯一,元素哈希不可变
- 集合是可变的
添:
s.update("3456") #迭代添加
s.add("元素") 单纯添加
删:
s.pop() 随机删除
s.remove("元素") 通过元素删除
s.clear() 清空
del s 删除整个集合
改:
删了再加
查:
for 循环
去重
li = {1,1,2,3,4,5,6,6,7,7}
print(list(set(li)))
各种集合
差集 s1-s2
并集 s1 | s2
交集 s1 & s2
对称差集--反交集 s1 ^ s2
print(s1 > s2) 超集 判断s2是不是s1的子集
冻结集合
可变转换成不可变
frozenset({1,2,3,4,5})
浅拷贝
浅拷贝会创建一个新的列表,列表中的元素和列表共用一份
浅拷贝会创建一个新的列表(容器)
新创建的列表中的元素和原列表的元素用的是同一个内存空间
浅拷贝:只拷贝第一层
会创建一个新的容器,两个列表公用一份地址
修改不可变数据类型,不变动,修改可变数据类型,变动
深拷贝 :拷贝了之后,就和之前的拷贝目标没什么关系,地址不同,修改不变动
- 赋值: 两个变量使用的是同一个空间
- 浅拷贝:修改不可变数据类型,不变动,修改可变数据类型,变动
- 深拷贝:修改就不变动
不可变数据类型更改后地址发生改变,可变数据类型更改地址不发生改变
| 数据类型 | 可变/不可变 |
|---|---|
| 整型 int=123 | 不可变 |
| 字符串 str= "123" | 不可变 |
| 元组 tuple=("123",[1,2,3]) | 不可变 |
| 列表 list=[1,2,3] | 可变 |
| 集合 set={1,2,3} | 可变 |
| 字典 dict={a:1,b:2,c:3} | 可变 |
dic = {} # "v":4
li = [] #[{"v":0},{"v":1},{"v":2},{"v":3},{"v":4}]
for i in range(0,5):
dic["v"] = i
li.append(dic)
print(li)
深拷贝:
import copy
li = [3,4,5,[1,2,3,4],6,7,8,{"k":'v'}]
l2 = copy.deepcopy(li)
li[-1]['k'] = "a"
print(li)
print(l2)