P1004 方格取数

P1004 方格取数

我们做题的思路可以这样：

①先看一下出题日期（毕竟是NOIP的题目，有一定的水准），然后发现是2000年的普及第四题

我们要知道的是，好像比较前面的几年由于1999的数塔IOI问题后，接下来几年的最后一两题都很喜欢出DP

所以，我们首先看一下题目的内容，求路径最大的方法，这时候就要想到DP或者DFS

②然后我们发现题目的数据规模不大，n<=9，所以我们可以考虑用DFS或者DP都可以

但是鉴于 "好像比较前面的几年由于1999的数塔IOI问题后，接下来几年的最后一两题都很喜欢出DP "

我们觉得用DP会比较好

③而且，NOIP的压轴DP题你想要2维过（在考场上是很难想出来的）

所以我们考虑高维

④我们找到一个东西叫做四维DP，因为这题是两个人走，我们思考一下能不能单纯用两个人的模拟过呢？

显然是可以的，我们记f[i][j][k][l]表示第1条路线的i,j走法和第2条路线的k,l走法

显然我们可以两个人一起走，复杂度最多就是9*9*9*9=6561（哈哈哈时间复杂度这么低）

所以我们就用这个方法了！

⑤然后我们思考动归方程的写法：

第1条路线只可能是从i-1,j或者i,j-1转移，第2条路线也只可能从k-1,l或者k,l-1转移

而且因为是2个人走，如果走到一点我们的那个点就要打标记说那点上面的值为0

所以我们得到了我们的动归方程（注意：万一i,j与k,l相同这是要小心的！）

f[i][j][k][l]=max(f[i-1][j][k-1][l],f[i][j-1][k-1][l],f[i-1][j][k][l-1],f[i][j-1][k][l-1])+a[i][j]+a[k][l];

#include<bits/stdc++.h>
using namespace std;
int n,x,y,val,ans=0,maxn,f[12][12][12][12],a[12][12];//a[i][j][k][l]表示两个人同时走，一个走i,j 一个走k,l 
int main(){
    scanf("%d",&n);
    memset(a,0,sizeof a);
    while(1){
        scanf("%d%d%d",&x,&y,&val);
        if(x==0&&y==0&&val==0)break;
        a[x][y]=val;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            for(int k=1;k<=n;k++){
                for(int l=1;l<=n;l++){
                    f[i][j][k][l]=max(f[i-1][j][k-1][l],max(f[i][j-1][k-1][l],max(f[i-1][j][k][l-1],f[i][j-1][k][l-1])))+a[i][j]+a[k][l];
                    if(i==k&&j==l)f[i][j][k][l]-=a[i][j];
                }
            }
        }
    }
    printf("%d
",f[n][n][n][n]);
    return 0;
}

看了下题解还没有spfa的费用流解法，就自己发一份了。来自一位不会动规的蒟蒻。

简要介绍一下如何构图

1. 拆点：因为每个方格只取一次，但要走两遍，因此我们考虑对于矩阵中每个方格拆为两个节点，一个为流入点，记为i；一个为流出点，记为i'。连两条边从i->i’，两条容量都为1，费用为-g[i][j]和0。

2. 编号：这个大家有各自的习惯。我的题解中具体看我程序中的hashin和hashout函数和注释，hashin用于编号我前文所提到的i，hashout用于编号我前文所提到的i'。

3. 连接节点：每个节点的out连接它的右边和它下边节点的流入点，对于边界特殊处理一下，s连(0,0)的入点，(n-1,n-1)连t点。

这样构图跑一遍spfa的最小费用最大流就OK了。

#include <cstdio>
#include <cstring>
#include <queue>
#define INF 0x7f7f7f7f
using namespace std;

struct Edge{
    int u;//大多数算法在邻接表中并不需要这个，但费用流比较例外
    int v;
    int f;//残量 
    int c;//费用 
    int next;
}e[850];//网络流的题目都要记得边数开两倍，因为还有反向弧
int head[170];
int n,m,s,t;
int ecnt = 0;
inline void AddEdge(int _u,int _v,int _f,int _c) {
    e[ecnt].next = head[_u];
    head[_u] = ecnt;
    e[ecnt].u = _u;
    e[ecnt].v = _v;
    e[ecnt].f = _f;
    e[ecnt].c = _c;
    ecnt++;
}
inline void Add(int _u,int _v,int _f,int _c) {
    AddEdge(_u,_v,_f,_c);
    AddEdge(_v,_u,0,-_c);
}

int dis[170];
bool inq[170];
int pre[170];
bool SPFA() {
    queue <int> q;
    q.push(s);
    memset(dis,0x7f,sizeof(dis));
    memset(inq,0,sizeof(inq));
    memset(pre,-1,sizeof(pre));
    inq[s] = true;
    dis[s] = 0;
    while (!q.empty()) {
        int cur = q.front();
        q.pop();
        inq[cur] = false;
        for (int i = head[cur];i != -1;i = e[i].next) {
            if (e[i].f != 0 && dis[e[i].v] > dis[cur] + e[i].c) {
                dis[e[i].v] = dis[cur] + e[i].c;
                pre[e[i].v] = i;
                if (!inq[e[i].v]) {
                    inq[e[i].v] = true;
                    q.push(e[i].v);
                }
            }
        }
    }
    return dis[t] != INF;
}

void MICMAF(int &flow,int &cost) {
    flow = 0;
    cost = 0;
    while (SPFA()) {
        int minF = INF;
        for (int i=pre[t];i != -1;i=pre[e[i].u]) minF = min(minF,e[i].f);
        flow += minF;
        for (int i=pre[t];i != -1;i=pre[e[i].u]) {
            e[i].f -= minF;
            e[i^1].f += minF;
        }
        cost += dis[t] * minF;
    }
}
/*
节点编号规则：
源点：0
矩阵节点(入)：n*x+y+1
矩阵节点(出)：n*n+n*x+y+1
汇点：2*n*n+1
*/
int g[10][10];
inline int hashin(int x,int y) {
    return n*x+y+1;
}
inline int hashout(int x,int y) {
    return n*n + n * x + y + 1;
}
int main() {
    memset(head,-1,sizeof(head));
    scanf("%d",&n);
    int x,y,v;
    while (scanf("%d%d%d",&x,&y,&v) == 3) {
        if (x == 0 && y == 0 && v == 0) break;
        x --;
        y --;
        g[x][y] = v;
    }
    s = 0;
    t = 2 * n * n + 1;
    Add(s,1,2,0);
    Add(2*n*n,t,2,0);
    for (int i=0;i<n;i++)
        for (int j=0;j<n;j++) {
            int in = hashin(i,j);
            int out = hashout(i,j);
            Add(in,out,1,0);//邻接表中后插入的先遍历，卡常，f=1是因为只可能再经过一次
            Add(in,out,1,-g[i][j]);
            if (i != n - 1) Add(out,hashin(i+1,j),2,0);
            if (j != n - 1) Add(out,hashin(i,j+1),2,0);
        }
    int f,c;
    MICMAF(f,c);
    printf("%d
",-c);
    return 0;
}

深搜深搜

见都是动规的帖子，来来来，贴一个深搜的题解（手动滑稽）。。。

这道题深搜的最优方法就是两种方案同时从起点出发。因为如果记录完第一种方案，再计算第二种方案，不可控的因素太多了，大多都不是最优解→_→，但两种方案同时执行就行，因为这可以根据当前的情况来判断最优。

总的来说，每走一步都会有四个分支（你理解成选择或者情况也可以）：

1、两种都向下走

2、第一种向下走，第二种向右走

3、第一种向右走，第二种向下走

4、两种都向右走

每走一步走枚举一下这四种情况，因为在每个点的方案具有唯一性（也就是在某个点走到终点的取数方案只有一个最优解，自己理解一下），所以我们可以开一个数组来记录每一种情况，当重复枚举到一种情况时就直接返回（对，就是剪枝），大大节省了时间（不然会超时哦~）。深搜和动归的时间复杂度时一样的！

#include<iostream>
    using namespace std;
    int N=0;
    int s[15][15],f[11][11][11][11];
int dfs(int x,int y,int x2,int y2)//两种方案同时执行，表示当第一种方案走到x,y,第二种方案走到x2,y2时到终点取得的最大数 
{
    if (f[x][y][x2][y2]!=-1) return f[x][y][x2][y2];//如果这种情况已经被记录过了，直接返回，节省时间 
    if (x==N&&y==N&&x2==N&&y2==N) return 0;//如果两种方案都走到了终点，返回结束 
    int M=0;
    //如果两种方案都不在最后一列，就都往下走，统计取得的数，如果有重复，就减去一部分 
    if (x<N&&x2<N) M=max(M,dfs(x+1,y,x2+1,y2)+s[x+1][y]+s[x2+1][y2]-s[x+1][y]*(x+1==x2+1&&y==y2));
    //如果第一种方案不在最后一行，第二种方案不在最后一列，第一种就向下走，第二种就向右走， 
    //统计取得的数，如果有重复，就减去一部分
    if (x<N&&y2<N) M=max(M,dfs(x+1,y,x2,y2+1)+s[x+1][y]+s[x2][y2+1]-s[x+1][y]*(x+1==x2&&y==y2+1));
    //如果第一种方案不在最后一列，第二种方案不在最后一行，第一种就向右走，第二种就向下走， 
    //统计取得的数，如果有重复，就减去一部分
    if (y<N&&x2<N) M=max(M,dfs(x,y+1,x2+1,y2)+s[x][y+1]+s[x2+1][y2]-s[x][y+1]*(x==x2+1&&y+1==y2));
    //如果第一种方案和第二种方案都不在最后一列，就都向右走，统计取得的数，如果有重复，就减去一部分
    if (y<N&&y2<N) M=max(M,dfs(x,y+1,x2,y2+1)+s[x][y+1]+s[x2][y2+1]-s[x][y+1]*(x==x2&&y+1==y2+1));
    //对最后那个 s[x][y+1]*(x==x2&&y+1==y2+1))的解释：这个是用来判断两种方案是不是走到了同一格的
    //如果是真，就返回1，否则返回0，如果是1的话，理所当然的可以减去s[x][y+1]*1,否则减去s[x][y+1]*0相当于
    //不减,写得有点精简，省了4个if，见谅哈~ 
    f[x][y][x2][y2]=M;//记录这种情况 
    return M;//返回最大值 
}
int main()
{
    cin>>N;
    //将记录数组初始化成-1，因为可能出现取的数为0的情况，如果直接判断f[x][y][x2][y2]!=0（见dfs第一行）
    //可能出现死循环而导致超时，细节问题 
    for(int a=0;a<=N;a++)
      for(int b=0;b<=N;b++)
        for(int c=0;c<=N;c++)
          for(int d=0;d<=N;d++) f[a][b][c][d]=-1;
    for(;;)//读入 
    {
        int t1=0,t2=0,t3=0;
        cin>>t1>>t2>>t3;
        if(t1==0&&t2==0&&t3==0) break;
        s[t1][t2]=t3;
    }
    cout<<dfs(1,1,1,1)+s[1][1];//输出，因为dfs中没有考虑第一格，即s[1][1]，所以最后要加一下 
    return 0;
}

设两个起点，总起点向副起点连一条容量为二，费用为零的边（只走两次）

用结构体存储每个费用不为零的点的信息（id是第几个被输入）

每个费用不为零的点又分为入点和出点，入出点之间连一条容量为一，费用为当前点权值的边（取走这个点的值），再连一条容量为二，费用为零的边（不取走这个点的值）

副起点向每个费用不为零的入点连一条容量为inf，费用为零的边

每个费用不为零的点的出点向终点连一条容量为inf，费用为零的边

每个费用不为零的点的出点只需要连与当前点最“近”的点的入点（需要排序）

详细说明请见下文：

下面来自wjyyy大神题解

对于坐标系中一个点，它可以由横坐标非严格小于它，且纵坐标非严格小于它的点（在可行域中）转移。我们为了控制边数，只用连接与它最近的点。我们在可行域中首先找到横坐标最大（同等条件下纵坐标最大）的点，接着屏蔽掉以原点与这个点的连线为对角线的矩形，因为矩形中的点都可以或直接或间接地转移到这个右上角点来：

我们依次这样做下去，就会得到这两个蓝色点和红色点，从蓝点指向红点是一条边权为∞，费用为0的承接边。

 

不过，在某些情况下，下面剩的两个黑点直接走到红点是更优的解，这样我们只需要把之前拆的点之间重新建一条边，边权为∞，费用为0的承接边，表示不经过这个点的两点连线通过这个点连接到一起，与这个点无关。这样一来，与上面的拆点一起，每个点有了两条自环边，实则分成了两个点，它们之间有两条连线，一条是承接边，一条是费用边，即对费用增加有贡献的边。

最后跑最大费用最大流即可

#include<bits/stdc++.h>
#define maxn 200000
#define inf INT_MAX
using namespace std;
struct edge{
    int x,y,f,v,next;
}e[maxn*10];
bool vis[maxn];
int n,m=1,cnt=0,mc=0;
int head[maxn],pre[maxn],sum[maxn];
inline void add(int a,int b,int c,int d){
    e[cnt].x=a; 
    e[cnt].y=b;
    e[cnt].f=c;
    e[cnt].v=d;
    e[cnt].next=head[a];
    head[a]=cnt++;
}
inline void ad(int a,int b,int c,int d){
    add(a,b,c,d);
    add(b,a,0,-d);
}
void init() {
    cnt=0;memset(head,-1,sizeof(head));
}
bool spfa(int s,int t){
    queue<int>q;
    for(int i=0;i<=t+1;i++){
        sum[i]=-inf;
        pre[i]=-1;
        vis[i]=0;
    }
    sum[s]=0;
    vis[s]=1;
    q.push(s);
    while(!q.empty()){
        int x=q.front(); q.pop(); vis[x]=0;
        for(int i=head[x];i!=-1;i=e[i].next){
            int y=e[i].y;
            int f=e[i].f;
            int v=e[i].v;
            if(f>0&&sum[y]<sum[x]+v){
                pre[y]=i;
                sum[y]=sum[x]+v;
                if(!vis[y]){
                    vis[y]=1;
                    q.push(y);
                }
            }
        }
    }
    return sum[t]>0;
}
void ek(int s,int t){
    mc=0;
    while(spfa(s,t)){
        int minn=inf;
        for(int i=pre[t];i!=-1;i=pre[e[i].x])
        minn=min(minn,e[i].f);
        mc+=sum[t]*minn;
        for(int i=pre[t];i!=-1;i=pre[e[i].x]){
            e[i].f-=minn;
            e[i^1].f+=minn;
        }
    }
    printf("%d",mc);
}
struct data{
    int x,y,z,id;
}bean[2005];
bool cmp(data a,data b){
    if(a.x==b.x) return a.y<b.y;
    return a.x<b.x;
}
int main()
{
    init();
    scanf("%d",&n);
    int s=0,t,ss;
    while(scanf("%d%d%d",&bean[m].x,&bean[m].y,&bean[m].z)){
        if(bean[m].x==0&&bean[m].y==0&&bean[m].z==0) break;
        bean[m].id=m; 
        m++;
    }
    m--;
    t=m*2+1;
    ss=t+1;
    ad(s,ss,2,0);
    for(int i=1;i<=m;i++){
        ad(ss,i,inf,0);
        ad(i+m,t,inf,0);
        ad(i,i+m,1,bean[i].z);
        ad(i,i+m,2,0); 
    }
    sort(bean+1,bean+m+1,cmp);
    for(int i=1;i<m;i++){
        int minn=inf;
        for(int j=i+1;j<=m;j++)
        if(bean[j].y>=bean[i].y&&bean[j].y<minn){
            minn=bean[j].y;
            ad(m+bean[i].id,bean[j].id,inf,0);
        }
    }
    ek(s,t);
}

本题是简单的双路动归。

---

注意到题目有一个设定，取走后的方格中的数字将变为0，如果没有这个设定，则可以考虑在搜索时求出最大值和次大值，相加即可。

一旦加上这个设定，则意味着对于大于0的格子只能取一次，所以直接在搜索时求最大值和次大值会出现错误。

题目要求是走两次，但是我们并不一定按部就班地一次一次地走，可以两条线路同时走！

假设某时刻走到(i,j)和(k,l)两个点，那么它们的来向就有四种可能: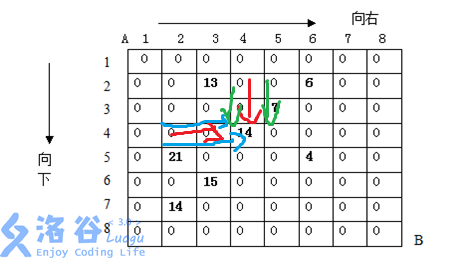 

1.同时从上方过来

2.从上方和左方过来

3.从左方和上方过来

4.同时从左方过来

由此可以推出状态转移方程

sum[i][j][k][l]表示两个点走到(i,j)和(k,l)时取得的最大值

sum[i][j][k][l]=max(
sum[i-1][j][k-1][l],
sum[i-1][j][k][l-1],
sum[i][j-1][k-1][l],
sum[i][j-1][k][l-1])
+fang[i][j]+(i==k&&j==l ? 0 : fang[k][l])

其中fang[i][j]为方格中有的数

#include<iostream>
using namespace std;
int fang[15][15],sum[15][15][15][15];
int max_(int a,int b,int c,int d)//max_() 是我手打的一个判断四个数中最大那个数的那个数的函数
{
    if(a<b)a=b;
    if(a<c)a=c;
    if(a<d)a=d;
    return a;
}
int main()//主函数
{
    int n;
    cin>>n;
    int x,y,c;
    cin>>x>>y>>c;
    while(x!=0 and y!=0 and c!=0){//读入，读到0停止
        fang[x][y]=c;
        cin>>x>>y>>c;
    }

    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            for(int k=1;k<=n;k++)
                for(int l=1;l<=n;l++)//四重循环动归
                    sum[i][j][k][l]=max_(
                    sum[i-1][j][k-1][l],//1.同时从上方过来
                    sum[i-1][j][k][l-1],//2.从上方和左方过来
                    sum[i][j-1][k-1][l],//3.从左方和上方过来
                    sum[i][j-1][k][l-1])//4.同时从左方过来 
                    +fang[i][j]+(i==k&&j==l ? 0 : fang[k][l]);//如果同时走到同一个点就不重复加了 
    cout<<sum[n][n][n][n];
    return 0;
}