描述
小Hi和小Ho所在学校的校园网被黑客入侵并投放了病毒。这事在校内BBS上立刻引起了大家的讨论,当然小Hi和小Ho也参与到了其中。从大家各自了解的情况中,小Hi和小Ho整理得到了以下的信息:
- 校园网主干是由N个节点(编号1..N)组成,这些节点之间有一些单向的网路连接。若存在一条网路连接(u,v)链接了节点u和节点v,则节点u可以向节点v发送信息,但是节点v不能通过该链接向节点u发送信息。
- 在刚感染病毒时,校园网立刻切断了一些网络链接,恰好使得剩下网络连接不存在环,避免了节点被反复感染。也就是说从节点i扩散出的病毒,一定不会再回到节点i。
- 当1个病毒感染了节点后,它并不会检查这个节点是否被感染,而是直接将自身的拷贝向所有邻居节点发送,它自身则会留在当前节点。所以一个节点有可能存在多个病毒。
- 现在已经知道黑客在一开始在K个节点上分别投放了一个病毒。
举个例子,假设切断部分网络连接后学校网络如下图所示,由4个节点和4条链接构成。最开始只有节点1上有病毒。
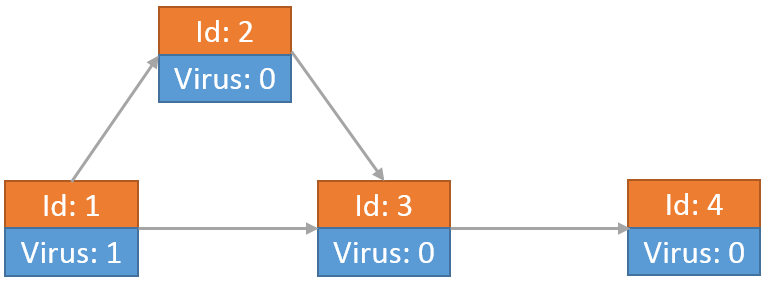
最开始节点1向节点2和节点3传送了病毒,自身留有1个病毒:
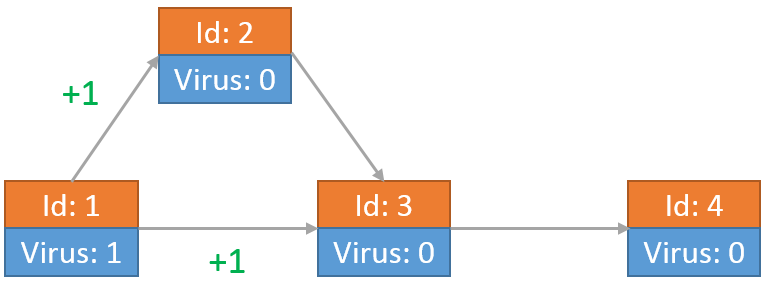
其中一个病毒到达节点2后,向节点3传送了一个病毒。另一个到达节点3的病毒向节点4发送自己的拷贝:
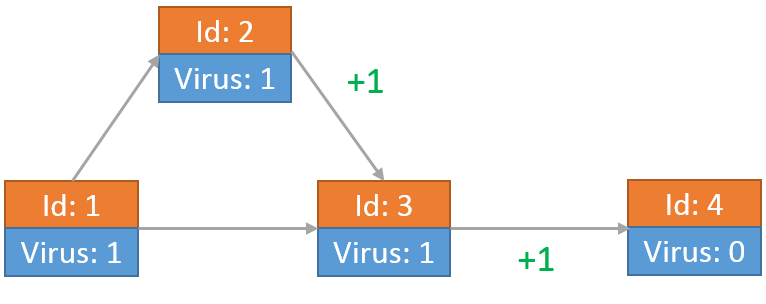
当从节点2传送到节点3的病毒到达之后,该病毒又发送了一份自己的拷贝向节点4。此时节点3上留有2个病毒:
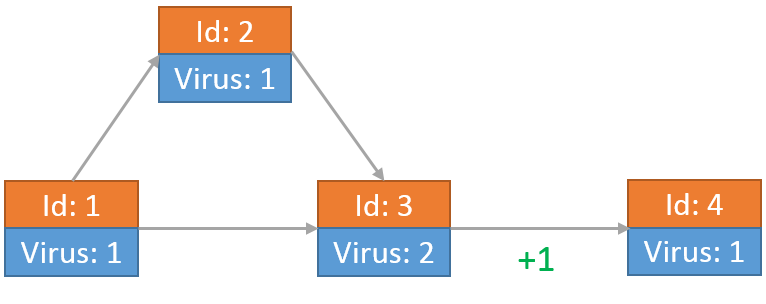
最后每个节点上的病毒为:
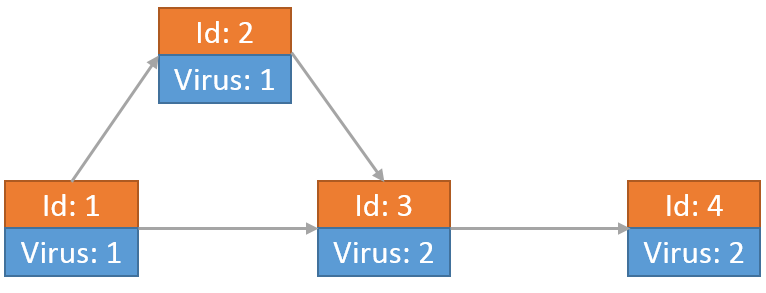
小Hi和小Ho根据目前的情况发现一段时间之后,所有的节点病毒数量一定不会再发生变化。那么对于整个网络来说,最后会有多少个病毒呢?
输入
第1行:3个整数N,M,K,1≤K≤N≤100,000,1≤M≤500,000
第2行:K个整数A[i],A[i]表示黑客在节点A[i]上放了1个病毒。1≤A[i]≤N
第3..M+2行:每行2个整数 u,v,表示存在一条从节点u到节点v的网络链接。数据保证为无环图。1≤u,v≤N
输出
第1行:1个整数,表示最后整个网络的病毒数量 MOD 142857
样例输入
4 4 1 1 1 2 1 3 2 3 3 4
样例输出
6
解题思路:这道还是拓扑排序裸题,题目已经保证是有向无环图。要求每次出队队首元素,都要将本身所带病毒数传给其所有邻接点。最后计算所有节点编号的总病毒数。简单题,注意两数相加时要取余,避免数据溢出!
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=100005; 4 const int mod=142857; 5 vector<int> vec[maxn];//邻接表,每个节点保存与它相连的边的另一个端点 6 queue<int> que; 7 int n,m,k,x,u,v,InDeg[maxn],virus[maxn];//记录每个节点的入度,num用来表示节点的个数,virus数组用来记录每个节点的病毒个数 8 void topsort(){ 9 for(int i=1;i<=n;++i) 10 if(!InDeg[i])que.push(i);//预处理,先将入度为0的节点编号入队 11 while(!que.empty()){ 12 int now=que.front();que.pop();//出队入度为0的编号节点 13 for(unsigned int i=0;i<vec[now].size();++i){ 14 if(--InDeg[vec[now][i]]==0)que.push(vec[now][i]); 15 virus[vec[now][i]]=(virus[now]+virus[vec[now][i]])%mod;//注意取余操作,避免数据溢出 16 } 17 } 18 } 19 int main() 20 { 21 while(cin>>n>>m>>k){ 22 for(int i=1;i<=n;++i)vec[i].clear();//全部清空 23 memset(InDeg,0,sizeof(InDeg));//全部顶点的度清0 24 memset(virus,0,sizeof(virus)); 25 while(k--){cin>>x;virus[x]++;} 26 while(m--){ 27 cin>>u>>v; 28 vec[u].push_back(v);//u指向v 29 InDeg[v]++;//v的入度加1 30 } 31 topsort(); 32 int sum=0;//保存所有节点病毒的总个数 33 for(int i=1;i<=n;++i)sum=(sum+virus[i])%mod; 34 cout<<sum<<endl; 35 } 36 return 0; 37 }