原文地址:http://www.cnblogs.com/zsboy/archive/2013/01/27/2878810.html
网络流看了两天,终于有了一点眉目,也拿模版A了道题目,通过对于模版代码的调试也真正了解了ek算法的用途了。
想好好写下总结都不让人顺心,写到一半网站死了,又得重新写。。
不说废话了,直接正题
首先要先清楚最大流的含义,就是说从源点到经过的所有路径的最终到达汇点的所有流量和
EK算法的核心
反复寻找源点s到汇点t之间的增广路径,若有,找出增广路径上每一段[容量-流量]的最小值delta,若无,则结束。
在寻找增广路径时,可以用BFS来找,并且更新残留网络的值(涉及到反向边)。
而找到delta后,则使最大流值加上delta,更新为当前的最大流值。
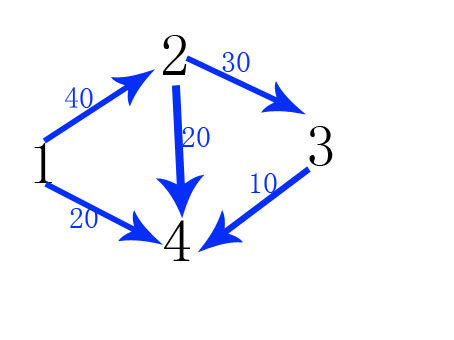
这么一个图,求源点1,到汇点3的最大流
由于我是通过模版真正理解ek的含义,所以先上代码,通过分析代码,来详细叙述ek算法
显而易见capacity存变的流量,进行ek求解
对于BFS找增广路:
1. flow[1]=INF,pre[1]=0;
源点1进队列,开始找增广路,capacity[1][2]=40>0,则flow[2]=min(flow[1],40)=40;
capacity[1][4]=20>0,则flow[4]=min(flow[1],20)=20;
capacity[2][3]=30>0,则flow[3]=min(folw[2]=40,30)=30;
capacity[2][4]=30,但是pre[4]=1(已经在capacity[1][4]这遍历过4号点了)
capacity[3][4].....
当index=4(汇点),结束增广路的寻找
传递回increasement(该路径的流),利用前驱pre寻找路径
路径也自然变成了这样:

2.flow[1]=INF,pre[1]=0;
源点1进队列,开始找增广路,capacity[1][2]=40>0,则flow[2]=min(flow[1],40)=40;
capacity[1][4]=0!>0,跳过
capacity[2][3]=30>0,则flow[3]=min(folw[2]=40,30)=30;
capacity[2][4]=30,pre[4]=2,则flow[2][4]=min(flow[2]=40,20)=20;
capacity[3][4].....
当index=4(汇点),结束增广路的寻找
传递回increasement(该路径的流),利用前驱pre寻找路径
图也被改成

接下来同理
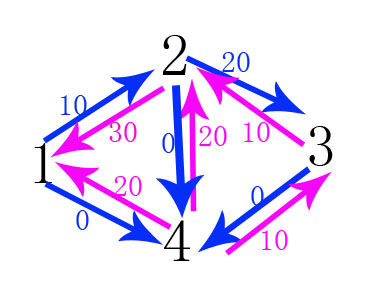
这就是最终完成的图,最终sumflow=20+20+10=50(这个就是最大流的值)
PS,为什么要有反向边呢?

我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。于是我们修改后得到了下面这个流。(图中的数字是容量)

这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?问题就在于我们没有给程序一个”后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢?回溯搜索吗?那么我们的效率就上升到指数级了。
而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时,inc(c[y,x],delta)
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下
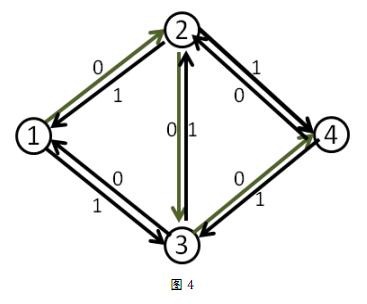
这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。

那么,这么做为什么会是对的呢?我来通俗的解释一下吧。
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给”退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。(有人问如果这里没有2-4怎么办,这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流量。
这就是这个算法的精华部分,利用反向边,使程序有了一个后悔和改正的机会。而这个算法和我刚才给出的代码相比只多了一句话而已。
至此,最大流Edmond-Karp算法介绍完毕。