SDUST-2017年12数据结构期末考试题（转载）

（1）考试时长2小时，从登录时间算起,12:10结束；（2）不想结束考试，千万不要点击结束考试，否则，后果自负；（3）考试期间只能使用PTA考试客户端、C、C++软件系统，严禁打开浏览器、通讯软件以及其他软件系统；违反以上规定以及学校的考试管理规定的以作弊论处（4）编程题禁止使用STL（5）如遇系统故障举手找监考

判断题答案： 1-5: T, F, T, T, F 6-10: T, F, T, F, F

选择题答案： 1-5: D, A, D, B, C 6-10: B, B, D, B, C

        11-15:  C,  B, B, C, B, C

判断题

1-1 图的关键路径上任意活动的延期都会引起工期的延长

1-2 所有的排序算法中，关键字的比较操作都是不可避免的

1-3 某二叉树的前序和中序遍历序列正好一样，则该二叉树中的任何结点一定都无左孩子

1-4 折半查找的判定树一定是平衡二叉树

1-5 查找某元素时，折半查找法的查找速度一定比顺序查找法快

1-6 用邻接矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关

1-7 基于比较的排序算法中，只要算法的最坏时间复杂度或者平均时间复杂度达到了次平方级O(N * logN)，则该排序算法一定是不稳定的

1-8 B-树中一个关键字只能在树中某一个节点上出现，且节点内部关键字是有序排列的

1-9 采用顺序存储结构的循环队列，出队操作会引起其余元素的移动

1-10 二叉树中至少存在一个度为2的结点

单选题

2-1 下面代码段的时间复杂度是

i = 1;
while( i<=n )
    i=i*3;

A. ({O(n)})

B. ({O(n​2​​)})

C. ({O(1)})

D. ({O(log​3​​n)})

2-2 设一段文本中包含4个对象{a,b,c,d}，其出现次数相应为{4,2,5,1}，则该段文本的哈夫曼编码比采用等长方式的编码节省了多少位数？

A.5

B.0

C.2

D.4

2-3 在双向循环链表结点p之后插入s的语句是:

A.s->prior=p;s->next=p->next; p->next=s; p->next->prior=s;

B.p->next=s;s->prior=p; p->next->prior=s ; s->next=p->next;

C.p->next->prior=s;p->next=s; s->prior=p; s->next=p->next;

D.s->prior=p;s->next=p->next; p->next->prior=s; p->next=s;

2-4 下图为一个AOV网，其可能的拓扑有序序列为

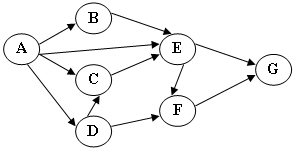
A.ABCDFE

B.ABCEDF

C.ACBDEF

D.ABCEFD

2-5对于模式串'abaaab'，利用KMP算法进行模式匹配时，其对应的Next取值（注意是未改进的Next值）为:

A.0 1 1 2 3 1

B.0 1 1 2 2 2

C.0 1 2 3 4 5

D.0 1 2 2 2 1

2-6 给定散列表大小为11，散列函数为H(Key)=Key%11。采用平方探测法处理冲突：h​i​​(k)=(H(k)±i​2​​)%11将关键字序列{ 6，25，39，61 }依次插入到散列表中。那么元素61存放在散列表中的位置是:

A.5

B.6

C.7

D.8

2-7 设栈S和队列Q的初始状态均为空，元素a、b、c、d、e、f、g依次进入栈S。若每个元素出栈后立即进入队列Q，且7个元素出队的顺序是b、d、c、f、e、a、g，则栈S的容量至少是

A.3

B.4

C.1

D.2

2-8 有组记录的排序码为{46，79，56，38，40，84 }，采用快速排序（以位于最左位置的对象为基准而）得到的第一次划分结果为：

A.{38,79,56,46,40,84}

B.{38,46,56,79,40,84}

C.{38,46,79,56,40,84}

D.{40,38,46,56,79,84}

2-9 设森林F中有三棵树，第一、第二、第三棵树的结点个数分别为M​1​​，M​2​​和M​3​​。则与森林F对应的二叉树根结点的右子树上的结点个数是：

A. M​1​​+M​2​​

B. M​2​​+M​3​​

C. M​1​​

D. M​3​​

2-10 在决定选取何种存储结构时，一般不考虑（）

A.结点个数的多少

B.对数据有哪些运算

C.所用编程语言实现这种结构是否方便

D.各结点的值如何

2-11 将{ 3, 8, 9, 1, 2, 6 }依次插入初始为空的二叉排序树。则该树的后序遍历结果是：

A. 1, 2, 8,6, 9, 3

B. 2,1, 6, 9, 8, 3

C. 1, 2, 3,6, 9, 8

D. 2, 1, 3,6, 9, 8

2-12 具有65个结点的完全二叉树其深度为（根的深度为1）：

A. 6

B. 5

C. 8

D. 7

2-13 在图中自d点开始进行深度优先遍历算法可能得到的结果为:

A. d,e,a,c,f,b

B. d,f,c,e,a,b

C. d,a,c,f,e,b

D. d,a,e,b,c,f

2-14 我们用一个有向图来表示航空公司所有航班的航线。下列哪种算法最适合解决找给定两城市间最经济的飞行路线问题？

A. Kruskal算法

B. Dijkstra算法

C. 深度优先搜索

D. 拓扑排序算法

2-15 若对N阶对称矩阵A以行优先存储的方式将其下三角形的元素(包括主对角线元素)依次存放于一维数组B［1..(N(N+1))/2］中，则A中第i行第j列（i和j从1开始，且i>j）的元素在B中的位序k（k从1开始）为 (3分)

A. j*(j-1)/2+i

B. i*(i+1)/2+j

C. j*(j+1)/2+i

D. i*(i-1)/2+j

函数题

6-1 删除单链表中最后一个与给定值相等的结点

本题要求在链表中删除最后一个数据域取值为x的节点。L是一个带头结点的单链表，函数ListLocateAndDel_L(LinkList L, ElemType x)要求在链表中查找最后一个数据域取值为x的节点并将其删除。例如，原单链表各个节点的数据域依次为1 3 1 4 3 5，则ListLocateAndDel_L(L,3)执行后，链表中剩余各个节点的数据域取值依次为1 3 1 4 5。

函数接口定义：

void ListLocateAndDel_L(LinkList L, ElemType x);

其中 L 是一个带头节点的单链表。 x 是一个给定的值。函数须在链表中定位最后一个数据域取值为x的节点并删除之。

裁判测试程序样例：

//库函数头文件包含
#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
//函数状态码定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
#define NULL 0

typedef int Status;
typedef int ElemType; //假设线性表中的元素均为整型

typedef struct LNode
{
    ElemType data;
    struct LNode *next;
} LNode, *LinkList;

//链表创建函数
Status ListCreate_L(LinkList &L, int n)
{
    LNode *rearPtr, *curPtr;
    L = (LNode *)malloc(sizeof(LNode));
    if (!L)
        exit(OVERFLOW);
    L->next = NULL;
    rearPtr = L;
    for (int i = 1; i <= n; i++)
    {
        curPtr = (LNode *)malloc(sizeof(LNode));
        if (!curPtr)
            exit(OVERFLOW);
        scanf("%d", &curPtr->data);
        curPtr->next = NULL;
        rearPtr->next = curPtr;
        rearPtr = curPtr;
    }
    return OK;
}

//链表输出函数
void ListPrint_L(LinkList L)
{
    LNode *p = L->next;
    if (!p)
    {
        printf("空表");
        return;
    }
    while (p != NULL)
    {
        if (p->next != NULL)
            printf("%d ", p->data);
        else
            printf("%d", p->data);
        p = p->next;
    }
}

//下面是需要实现的函数的声明
void ListLocateAndDel_L(LinkList L, ElemType x);

int main()
{
    LinkList L;
    int n;
    int x;
    scanf("%d", &n);
    //输入链表中元素个数

    if (ListCreate_L(L, n) != OK)
    {
        printf("表创建失败！！！
");
        return -1;
    }
    scanf("%d", &x); //输入待查找元素
    ListLocateAndDel_L(L, x);
    ListPrint_L(L);
    return 0;
}
/* 请在这里填写答案 */

输入样例：

6
1 3 1 4 3 5
3

输出样例：

1 3 1 4 5

答案:

void ListLocateAndDel_L(LinkList L, ElemType x)
{
    if(!L)
        return;//表空啥也不干
    else
    {
        LinkList p = L->next,q,t=L;//t指向头结点
        while(p)
        {
            if(p->data==x)
                t = q;//记录并更新相同位置（t也是要删除位置的直接前驱）
            q = p;//这两部就是不等就一直往后更新
            p = p->next;
        }
        if(t!=L)//大概的意思就是t往后移动了，就可以删了(不知道不写这句行不行)
        {
            t->next = t->next->next;//删除操作
        }
    }
}

6-2 计算二叉树的深度

编写函数计算二叉树的深度。二叉树采用二叉链表存储结构

函数接口定义：

int GetDepthOfBiTree ( BiTree T);

其中 T是用户传入的参数，表示二叉树根节点的地址。函数须返回二叉树的深度（也称为高度）。

裁判测试程序样例：

//头文件包含
#include <stdlib.h>
#include <stdio.h>
#include <malloc.h>
//函数状态码定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -1
#define INFEASIBLE -2
#define NULL 0
typedef int Status;
//二叉链表存储结构定义
typedef int TElemType;
typedef struct BiTNode
{
    TElemType data;
    struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;
//先序创建二叉树各结点，输入0代表空子树
Status CreateBiTree(BiTree &T)
{
    TElemType e;
    scanf("%d", &e);
    if (e == 0)
        T = NULL;
    else
    {
        T = (BiTree)malloc(sizeof(BiTNode));
        if (!T)
            exit(OVERFLOW);
        T->data = e;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
    return OK;
}
//下面是需要实现的函数的声明
int GetDepthOfBiTree(BiTree T);
//下面是主函数
int main()
{
    BiTree T;
    int depth;
    CreateBiTree(T);
    depth = GetDepthOfBiTree(T);
    printf("%d
", depth);
}
/*请在这里填写答案*/

输入样例(输入0代表创建空子树)：

1 3 0 0 5 7 0 0 0

输出样例：

3

编程题

7-1 排序

给定N个（长整型范围内的）整数，要求输出从小到大排序后的结果。

本题旨在测试各种不同的排序算法在各种数据情况下的表现。各组测试数据特点如下：

· 数据1：只有1个元素；

· 数据2：11个不相同的整数，测试基本正确性；

· 数据3：103个随机整数；

· 数据4：104个随机整数；

· 数据5：105个随机整数；

· 数据6：105个顺序整数；

· 数据7：105个逆序整数；

· 数据8：105个基本有序的整数；

· 数据9：105个随机正整数，每个数字不超过1000。

输入格式:

输入第一行给出正整数N（≤10​5​​），随后一行给出N个（长整型范围内的）整数，其间以空格分隔。

输出格式:

在一行中输出从小到大排序后的结果，数字间以1个空格分隔，行末不得有多余空格。

输入样例:

11

4 981 10 -17 0 -20 29 50 8 43 -5

输出样例:

-20 -17 -5 0 4 8 10 29 43 50 981

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <ctype.h>
#include <time.h>//我要搞事 (｀･ω･´)

#define max(A, B) ((A > B) ? A : B)
#define min(A, B) ((A < B) ? A : B)

void swap(int arr[], int i, int j);
void QuickSort(int arr[], int left, int right);
void ShellSort(int arr[], int left, int right);
void InsertSort(int arr[], int left, int right);
void BucketSort(int arr[], int left, int right);
void SelectSort(int arr[], int left, int right);
void Merge(int arr[], int left, int mid, int right);
void MergeSort(int arr[], int left, int right);

int main()
{
    int n;
    int *arr;
    int i;

    scanf("%d", &n);
    arr = (int*)malloc(sizeof(int) * (n + 1));
    for (i = 1; i <= n; i++)
        scanf("%d", arr + i);
    /*想测试人品吗？srand((unsigned)time(0));
    int temp = rand() % 6;   //骚一波 ≖‿≖✧ ps:拼人品，有可能过不了
    switch (temp) {
    case 0:
        QuickSort(arr, 1, n);
        break;
    case 1:
        ShellSort(arr, 1, n);
        break;
    case 2:
        InsertSort(arr, 1, n);
        break;
    case 3:
        BucketSort(arr, 1, n);
        break;
    case 4:
        SelectSort(arr, 1, n);
        break;
    case 5:
        MergeSort(arr, 1, n);
        break;
    default:
        printf("error: rand()? or mod Σ( ° △ °|||)︴
");
        break;
    }*/
    MergeSort(arr, 1, n);
    for (i = 1; i <= n; i++)
        printf("%d ", arr[i]);
    return 0;
}

void swap(int arr[], int i, int j)
{
    int temp;

    temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

void QuickSort(int arr[], int left, int right)
{
    int i, pivot;

    if (left >= right)
        return;
    pivot = left;
    swap(arr, left, (left + right) / 2);
    for (i = left + 1; i <= right; i++) //单边搜索，可以该为双向搜索（据说快点( ° ▽、° )）
        if (arr[i] < arr[left])
            swap(arr, i, ++pivot);
    swap(arr, left, pivot);
    QuickSort(arr, left, pivot - 1);
    QuickSort(arr, pivot + 1, right);
}

void ShellSort(int arr[], int left, int right)
{
    int gap, i, j;

//ShellSort因为我只写过0——n-1的(最标准的)，可能有点小bug（不过应该没错吧 (*´Д｀*) )
    for (gap = (left + right) / 2; gap > 0; gap /= 2)
        for (i = gap; i <= right; i++)
            for (j = i - gap; j > 0 && arr[j] > arr[j + gap]; j -= gap)
                swap(arr, j, j + gap);
}

void InsertSort(int arr[], int left, int right)
{
    int i, v;

    for (i = left; i <= right; i++) {
        v = arr[i];
        int l = left, r = i;
        int j;
        while (l < r) {//在l与r之间插入排序，可以理解为解决子问题1→2→...→n
            int mid = (l + r) / 2;
            if (arr[mid] <= v)
                l = mid + 1;
            else
                r = mid;
        }
        for (j = i - 1; l <= j; j--)
            arr[j + 1] = arr[j];
        arr[l] = v;
    }
}

void BucketSort(int arr[], int left, int right)
{
    int i, v;
    static int cnt[123456] = { 0 };

    for (i = left, v = 0; i <= right; i++) {
        v = max(v, arr[i]);//部分优化：统计最大值，不用遍历所有桶，但空间仍是个问题╮(╯▽╰)╭
        cnt[arr[i]]++;
    }
    v++;
    while (v-- > 0)
        while (cnt[v]-- > 0)
            arr[--i] = v;
}

void SelectSort(int arr[], int left, int right)
{
    int i, j, k;

    for (i = left; i <= right; i++) {
        for (j = k = i; j <= right; j++) //可以理解为对k进行选择，将k的指向第i-left小的
            if (arr[j] < arr[k])
                k = j;
        if (i < k)
            swap(arr, i, k);
    }
}

void Merge(int arr[], int left, int mid, int right)
{
    //merge arr[L,M](sorted) and arr(M,R](sorted) into arr[L,R]
    static int p = 1, que[123456] = { 0 };
    int pl = left, pr = mid;
    int ql = mid + 1, qr = right;

    while (pl <= pr || ql <= qr) {
        if ((ql > qr) || (pl <= pr && arr[pl] <= arr[ql])) //有点麻烦的判断，要考虑arr已提取完的情况
            que[p++] = arr[pl++];
        else
            que[p++] = arr[ql++];
    }
    while (left <= right)
        arr[right--] = que[--p];
}

void MergeSort(int arr[], int left, int right)
{
    if (left >= right)
        return;
    int mid = (left + right) / 2;
    MergeSort(arr, left, mid);
    MergeSort(arr, mid + 1, right);
    Merge(arr, left, mid, right);//二分递归
}

转载自:https://blog.csdn.net/weixin_42110638/article/details/85146619与https://www.luogu.org/blog/hardictdbsd/solution-p1177