题目描述
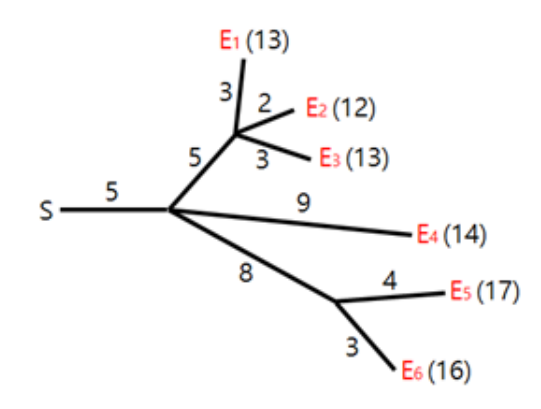
烟花表演是最引人注目的节日活动之一。在表演中,所有的烟花必须同时爆炸。为了确保安全,烟花被安置在远离开关的位置上,通过一些导火索与开关相连。导火索的连接方式形成一棵树,烟花是树叶,如图所示。火花从开关出发,沿导火索移动。每当火花抵达一个分叉点时,它会扩散到与之相连的所有导火索,继续燃烧。导火索燃烧的速度是一个固定常数。图中展示了六枚烟花 {E_1, E_2, dots, E_6}{E1,E2,…,E6} 的连线布局,以及每根导火索的长度。图中还标注了当在时刻 00 从开关点燃火花时,每一发烟花的爆炸时间。
Hyunmin 为烟花表演设计了导火索的连线布局。不幸的是,在他设计的布局中,烟花不一定同时爆炸。我们希望修改一些导火索的长度,让所有烟花在同一时刻爆炸。例如,为了让图中的所有烟花在时刻 1313 爆炸,我们可以像下图中左边那样调整导火索长度。类似地,为了让图中的所有烟花在时刻 1414 爆炸,我们可以像下图中右边那样调整长度。
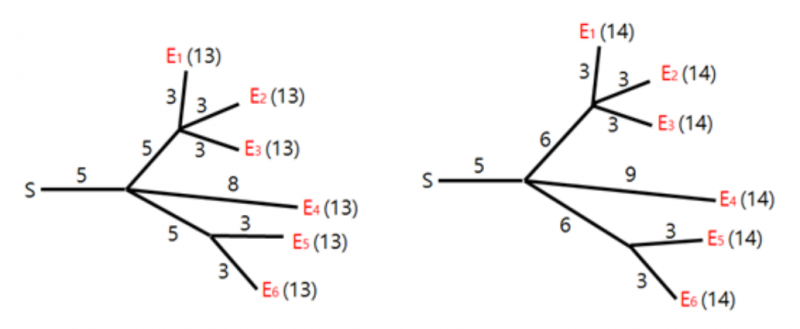
修改导火索长度的代价等于修改前后长度之差的绝对值。例如,将上面那副图中布局修改为下面那副图的左边布局的总代价为 66 ,而修改为右边布局的总代价为 55 。
导火索的长度可以被减为 00 ,同时保持连通性不变。
给定一个导火索的连线布局,你需要编写一个程序,去调整导火索长度,让所有的烟花在同一时刻爆炸,并使得代价最小。
输入输出格式
输入格式:
所有的输入均为正整数。令 NN 代表分叉点的数量, MM 代表烟花的数量。分叉点从 11 到 NN 编号,编号为 11 的分叉点是开关。烟花从 N + 1N+1 到 N + MN+M 编号。
输入第一行为 N, MN,M 。后面 N + M - 1N+M−1 行,第 ii 行两个整数 P_{i + 1}, C_{i + 1}Pi+1,Ci+1 。其中 P_iPi 满足 1 leq P_i < i1≤Pi<i ,代表和分叉点或烟花 ii 相连的分叉点。 C_iCi 代表连接它们的导火索长度( 1 leq C_i leq 10^91≤Ci≤109 )除开关外,每个分叉点和多于 11条导火索相连,而每发烟花恰好与 11 条导火索相连。
输出格式:
输出调整导火索长度,让所有烟花同时爆炸,所需要的最小代价。
输入输出样例
说明
【数据规模】
子任务 1(7 分): N = 1N=1 , 1 leq M leq 1001≤M≤100 。
子任务 2(19 分): 1 leq M leq 3001≤M≤300 ,且开关到任一烟花的距离不超过 300300 。
子任务 3(29 分): 1 leq M leq 50001≤M≤5000 。
子任务 4(45 分): 1 leq M leq 3000001≤M≤300000 。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 typedef long long lol; 8 int ch[1500001][2]; 9 lol tr[1500001],w[600001],sum; 10 int dis[1500001],fa[600001],son[600001],n,m,rt[600001],tot; 11 int merge(int a,int b) 12 { 13 if (!a||!b) return a^b; 14 if (tr[a]<tr[b]) swap(a,b); 15 ch[a][1]=merge(ch[a][1],b); 16 if (dis[ch[a][0]]<dis[ch[a][1]]) swap(ch[a][0],ch[a][1]); 17 if (ch[a][1]) 18 dis[a]=dis[ch[a][1]]+1; 19 else dis[a]=0; 20 return a; 21 } 22 int pop(int a) 23 { 24 return merge(ch[a][0],ch[a][1]); 25 } 26 int main() 27 {int i; 28 lol l,r; 29 cin>>n>>m; 30 for (i=2;i<=n+m;i++) 31 { 32 scanf("%d%lld",&fa[i],&w[i]); 33 son[fa[i]]++; 34 sum+=w[i]; 35 } 36 for (i=n+m;i>1;i--) 37 { 38 l=0;r=0; 39 if (i<=n) 40 { 41 while (--son[i]) rt[i]=pop(rt[i]); 42 l=tr[rt[i]];rt[i]=pop(rt[i]); 43 r=tr[rt[i]];rt[i]=pop(rt[i]); 44 } 45 tr[++tot]=l+w[i];tr[++tot]=r+w[i]; 46 rt[i]=merge(rt[i],merge(tot,tot-1)); 47 rt[fa[i]]=merge(rt[fa[i]],rt[i]); 48 } 49 while (son[1]--) rt[1]=pop(rt[1]); 50 while (rt[1]) 51 { 52 sum-=tr[rt[1]];rt[1]=pop(rt[1]); 53 } 54 cout<<sum; 55 }