明天开学
问题模型一般是:
给定n个物品,有一个容积为V的背包,每个物品依赖一个物品,选择一个必须选择所依赖的物品,依赖关系构成一棵树,每个物品有体积,价值,最大化价值;
这种模型称作树形有依赖背包问题;
常见方法大概有三种:
1.多叉树转化为二叉树:
将一个节点的多个儿子中选择最左的儿子保留下来,剩下的儿子放到左儿子的右子树里;
来张图片:
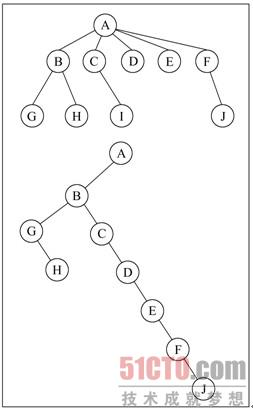
状态转移即为:
设dp[i][j]表示在以i为根的子树中,用大小为j的包能取得的最大价值,
dp[i][j]=max(dp[left[i]][j-w[i]]+v[i],dp[right[i]][j]);
left[i]是i在原树中的第一个儿子,right[i]是i在原树中的下一个兄弟。
第二种方法:dfs序表示法:
我们对于每一个节点求出他在原树中的dfs序dfn值,然后记录他的子数大小size;
那么对于一个节点x:x的第一个儿子y有dfn[y]=dfn[x]+1;
对于x的第二个儿子z,dfn[z]=dfn[x]+size[y]+1;
对于x的一个兄弟k,有dfn[k]=dfc[x]+size[x]+1;
一个dfs序为i的节点u,同样设dp[i][j]表示在以u为根的子树中,用大小为j的包能取得的最大价值,
dp[i][j]+w[i]->dp[i+1][j-v[i]]
dp[i][j]->dp[i+size[i]+1][j]
这也是较常用的刷表法,用当前状态更新后继的状态;
两种方法主要解决点权问题;
那么我们看一下用树形分组背包问题:
一道经典问题 选课:题目传送门;
题解(https://www.cnblogs.com/Tyouchie/p/10830072.html);
我们设dp[k][i][j]表示以i为根的子树,在前k个儿子中,选出一个大小为j的子树(必须包含i),所获得的最大学分。
那么我们每计算到第k+1个新的儿子v时(size[v]表示v的儿子个数),
dp[k+1][i][j]=min(dp[k][i][j-t]+dp[size[v]][v][t]);
k这一维显然可以无用的;
那么我们改为f[i][j]表示在以i为根的子树内选择了j门课程所获得的最大学分;
dp[i][j]=max(dp[i][j-t]+dp[v][t]);
j=m-1->1(m指容积,-1是因为当前点占据了1的体积);
t=1->j(在我那片题解中我倒序枚举了t,但是我发现两者都是正确的);
这个模型感觉要理解并且掌握,因为很多树形背包类dp的状态都是这样转移的;

#include<bits/stdc++.h> using namespace std; int lin[1000],tot,n,m,x,f[400][400],s[400]; template<typename T>inline void read(T &x) { x=0;T f=1,ch=getchar(); while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();} while(isdigit(ch)) {x=x*10+ch-'0'; ch=getchar();} x*=f; } struct gg { int y,next; }a[2000]; inline void add(int x,int y) { a[++tot].y=y; a[tot].next=lin[x]; lin[x]=tot; } inline void dp(int x) { f[x][0]=0; for(int i=lin[x];i;i=a[i].next) { int y=a[i].y; dp(y); for(int t=m;t>=0;--t) { for(int j=0;j<=t;++j) { if(t-j>=0) { f[x][t]=max(f[x][t],f[x][t-j]+f[y][j]); } } } } if(x!=0) { for(int t=m;t>0;t--) f[x][t]=f[x][t-1]+s[x]; } } int main() { read(n);read(m); for(int i=1;i<=n;i++) { read(x); add(x,i); read(s[i]); } dp(0); cout<<f[0][m]<<endl; return 0; }
f[i][j]表示以i为根的子树内分离一个大小为j的子树所需要的最少操作数;
j=p->1;
t=1->j;
和上一道题目很像;
显然f[x][1]为每个点x的度;
再转移的时候-2是因为u->v的边和v->u的边都已经在初始化的时候被减掉了,所以这时候要把他们连起来就得减去他们两个造成的贡献,也就是2.,思考一下,很好理解;

#include<bits/stdc++.h> using namespace std; template<typename T>inline void read(T &x) { x=0; T f=1,ch=getchar(); while (!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();} while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar(); x*=f; } const int N=250; struct gg { int y,next,v; }a[N<<1]; int n,p,tot,x,y,lin[N],du[250],dp[250][250]; inline void add(int x,int y) { a[++tot].y=y; a[tot].next=lin[x]; lin[x]=tot; } inline void dfs(int x,int fa) { dp[x][1]=du[x]; for(int i=lin[x];i;i=a[i].next) { int y=a[i].y; if(y==fa) continue; dfs(y,x); for(int j=p;j>=1;j--) { for(int t=1;t<=j;t++) { dp[x][j]=min(dp[x][j],dp[x][j-t]+dp[y][t]-2); } } } } int main() { read(n); read(p); for(int i=1;i<n;i++) { read(x); read(y); add(x,y); add(y,x); du[x]++; du[y]++; } memset(dp,0x3f,sizeof(dp)); dfs(1,0); int ans=1<<30; for(int i=1;i<=n;i++) { ans=min(ans,dp[i][p]); } cout<<ans<<endl; return 0; }
真正理解前两到题目这道也就不难了;
我们设f[i][j]表示在以i为根的子树内,让j个人看所获得的最大收益;
那么对于每一个叶子节点x,f[x][1]就等于val[x];
那么最后我们寻找一个最大的i满足f[1][i]>=0;
所以我们倒序扫描就行了;
状态转移是j,t的枚举和前两题是一样的;
根据当前背包容积转移;

#include<bits/stdc++.h> using namespace std; template<typename T>inline void read(T &x) { x=0; T f=1,ch=getchar(); while (!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();} while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar(); x*=f; } int n,m,dp[3010][3010],val[3010],k,x,v,tot,lin[3010]; struct gg { int y,next,v; }a[1000100]; inline void add(int x,int y,int v) { a[++tot].y=y; a[tot].next=lin[x]; lin[x]=tot; a[tot].v=v; } int dfs(int u) { if(u>n-m) { dp[u][1]=val[u]; return 1; } int sum=0,s,t; for(int i=lin[u];i;i=a[i].next) { int y=a[i].y; s=dfs(y); sum+=s; for(int j=sum;j>0;j--) { for(int t=1;t<=j;t++) { dp[u][j]=max(dp[u][j],dp[u][j-t]+dp[y][t]-a[i].v); } } } return sum; } int main() { memset(dp,0xcf,sizeof(dp)); read(n); read(m); for(int i=1;i<=n-m;i++) { read(k); for(int j=1;j<=k;j++) { read(x); read(v); add(i,x,v); } } for(int i=n-m+1;i<=n;i++) read(val[i]); for(int i=1;i<=n;i++) dp[i][0]=0; dfs(1); for(int i=m;i>=1;i--) if(dp[1][i]>=0) { printf("%d",i); break; } return 0; }
