分析问题
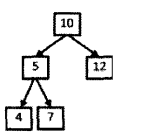
首先需要明白路径的概念,路径是从根节点出发,一直到叶子节点,所形成的一条路径
所以我们寻找和为某一值的路径的时候,首先从根节点10出发,前序遍历二叉树,路径为10,5,4,发现和不为22,所以需要从4返回到5,然后再走7,发现和为22,记录下这条路径
然后再返回到5,再返回到10,再从10的右子树开始,到12,又记录下一条路径
发现这是一个栈的结构,所以我们考虑用一个栈来存储路径,另外我们需要一个结果来存储currentSum,用于与exceptedSum相比较
解决问题
public void findPath(BinaryTreeNode root, int expectedSum,
Stack<Integer> path, int currentSum) {
if (root == null)
return;
currentSum += root.data;
path.push(root.data);
boolean isLeaf = root.leftNode == null && root.rightNode == null;
if (isLeaf) {
if (currentSum == expectedSum) {
System.out.println("A path is");
for (int i : path)
System.out.print(i+" ");
System.out.println();
}
} else {
if (root.leftNode != null) {
findPath(root.leftNode, expectedSum, path, currentSum);
}
if (root.rightNode != null) {
findPath(root.rightNode, expectedSum, path, currentSum);
}
}
currentSum -= root.data;
path.pop();
}
测试代码
MySo2 mySo2=new MySo2();
Stack path=new Stack<>();
int currentSum=0;
mySo2.findPath(root1, 22, path, currentSum);
首先创建一个stack用于存放路径,作为参数传入findpath中,另外也将currentSum作为参数传入
在findPath函数中,首先判断一下root是否为空,为空的话就没什么好玩儿的了
不为空,那么将currentSum加上root的值,表明现在的Sum,将root的值压入栈中,这里取了个巧,只压入了root的data值,而不是压入的节点
因为这里仅仅需要实现的一个功能是在递归返回上一层的时候,将节点从路径中删除,而返回上一层节点在递归的时候就已经实现了
对于路径来说,需要判断是否抵达叶子节点,叶子节点的定义是没有左右孩子,这里将对节点的判断用个boolean值来替代,使得代码简洁一些
如果是叶子节点,判断一下currentSum和exceptedSum是否相等,如果相等,将路径打印出来
如果不是叶子节点,那么就需要前序遍历递归到左子树,然后返回到上一层,递归到右子树
右子树返回的时候,需要将栈弹出,说明要将这个节点从路径中删除
实例说明
说一下上述树的递归过程吧,首先传入10,currentSum=10,将10压入栈中,10不是叶子节点,有左孩子5,进入到左子树,也就是递归的下一层,这时候的参数root=5,exceptedSum一直没变是22,这里后面不再说了,path中有10,currentSum=10,传进来之后,5不为空(其实这里每次都要判读一下不是很好,可以优化),currentSum要加上这个5,成为15,5压入栈中,5也不是叶子节点,继续进入左子树,为4,currentSum加上4,为19,4压入栈中,4是叶子节点,但是19不等于22,这里不会进入else了,就直接currentSum减去4,并将栈中的4弹出,此时栈中只有10和5,进入到5的右子树,同样的判断,和为22,打印出来,然后弹出7,返回到上一层,由于上一层已经执行到进入右子树那条语句,也就是if (root.rightNode != null) findPath(root.rightNode, expectedSum, path, currentSum);所以下一条应该执行的语句就是currentSum减去5,将5弹出,此时再返回上一层,也就是现在栈中只有10,由于在10这一层,只执行到
if (root.leftNode != null) findPath(root.leftNode, expectedSum, path, currentSum);这条语句,接下来应该执行进入右子树的语句了,接下来也就没什么好说的了