简述:
二叉树是十分重要的数据结构,主要用来存放数据,并且方便查找等操作,在很多地方有广泛的应用。
二叉树有很多种类,比如线索二叉树,二叉排序树,平衡二叉树等,本文写的是最基础最简单的二叉树。
思路:
二叉树的建立采用的是递归的思想:给定一个指向根节点的指针,然后递归调用ceate()函数,自动生成一个二叉树。就像是在地上挖了个坑(根节点)
,然后他会拿着铲子(create函数)按照一定的规则自动挖一个很大的洞穴(二叉树)出来。当然挖坑前需要先定义每个洞长什么样(定义节点结构)。
二叉树的遍历采用的也是递归的思想:如果节点有数据,则按照遍历规则打印根节点和孩子节点,没有数据则返回直到所有数据都遍历完,递归结束。
代码如下:
1 #include "stdafx.h" //我自己的编译器的问题所以要加 2 #include<iostream> 3 using namespace std; 4 typedef char TElemType; 5 typedef struct BiTNode { 6 TElemType data; 7 struct BiTNode *lchild, *rchild; 8 }BiTNode,*BiTree; //*BiTree的意思是给 struct BiTNode*起了个别名,叫BiTree,故BiTree为指向节点的指针。 9 10 void createBiTree(BiTree &T) //创建二叉树。 11 { 12 char ch; 13 cin >> ch; 14 if ('#' == ch) 15 T = NULL; 16 else 17 { 18 T = new BiTNode; 19 T->data = ch; 20 createBiTree(T->lchild); 21 createBiTree(T->rchild); 22 } 23 } 24 void PerOrderTraverse(BiTree T) //前序遍历二叉树并打印。 25 { 26 if (T) 27 { 28 cout << T->data<<" "; 29 PerOrderTraverse(T->lchild); 30 PerOrderTraverse(T->rchild); 31 } 32 } 33 34 void InOrderTraverse(BiTree T) //中序遍历二叉树并打印。 35 { 36 if (T) 37 { 38 InOrderTraverse(T->lchild); 39 cout << T->data<<" "; 40 InOrderTraverse(T->rchild); 41 } 42 } 43 44 void PostOrderTraverse(BiTree T) //后序遍历二叉树并打印。 45 { 46 if (T) 47 { 48 PostOrderTraverse(T->lchild); 49 PostOrderTraverse(T->rchild); 50 cout << T->data<<" "; 51 } 52 } 53 void Copy(BiTree T, BiTree &NewT) //二叉树的拷贝 54 { 55 if (T == NULL) 56 { 57 NewT = NULL; 58 return; 59 } 60 else 61 { 62 NewT = new BiTNode; 63 NewT->data = T->data; 64 cout << NewT->data<<" "; 65 Copy(T->lchild, NewT->lchild); 66 Copy(T->rchild, NewT->rchild); 67 68 } 69 } 70 71 int NodeCount(BiTree T) //求二叉树中结点个数 72 { 73 if (T == NULL) 74 return 0; 75 else 76 return NodeCount(T->lchild) + NodeCount(T->rchild) + 1; 77 } 78 79 int LeafCount(BiTree T) { 80 //求二叉树中叶子(终端节点)个数 81 if (T == NULL) 82 return 0; 83 if (T->lchild == NULL && T->rchild == NULL) 84 return 1; 85 else 86 return LeafCount(T->lchild) + LeafCount(T->rchild); 87 } 88 89 int main() 90 { 91 BiTree T; //声明一个指向二叉树根节点的指针 92 BiTree NewT; //声明一个指向二叉树根节点的NewT指针,用于复制T的内容 93 createBiTree(T); 94 cout << "二叉树创建完毕!" << endl; 95 cout << "二叉树中结点个数:" << endl; 96 cout<<NodeCount(T)<<endl; 97 cout << "二叉树中叶子个数:" << endl; 98 cout << LeafCount(T) << endl; 99 cout << "拷贝结果:" << endl; 100 Copy(T, NewT); 101 cout << endl; 102 cout << "前序遍历二叉树:" << endl; 103 PerOrderTraverse(T); 104 cout << endl; 105 cout << "中序遍历二叉树:" << endl; 106 InOrderTraverse(T); 107 cout << endl; 108 cout << "后序遍历二叉树:" << endl; 109 PostOrderTraverse(T); 110 cout << endl; 111 return 0; 112 }
测试样例+结果:
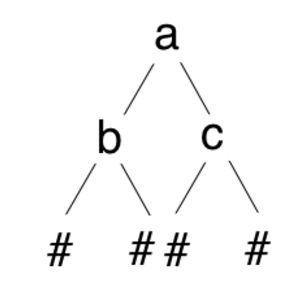
假设我们要建立一个如下图所示的二叉树,#代表空节点,按照前序遍历顺序二叉树表示为:ab##c## (此处为前序)
下面是代码的运行结果:
