废话不多说,直接看题。
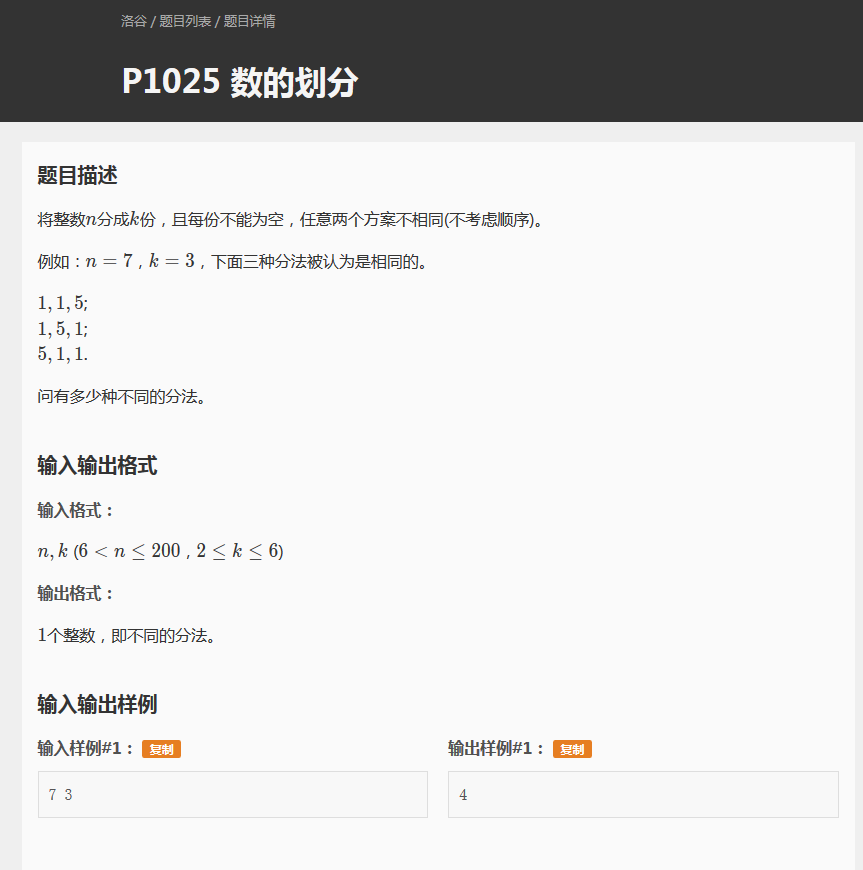
首先先来说明一下题意:具体就是说一共要分成k个数,它们的和为n,看到这你们会想到什么,小编第一眼就会想到小学/学前班学的东西,把一个数拆成两个数的和。如:
就像这样,只是情况有变,把一个数分成更多的数的和就OK了。
行了,扯的远了,回归正题,既然这道题出现在搜索中,就用搜索吧(其实其它方法也可以,隔壁Willian用三重循环强行打过)。
既然搜索,就先考虑一下用深搜还是广搜,就用深搜把(个人偏爱),那怎么搜呢?举个栗子以题目的栗子为栗,7怎么分?为了按顺序,那么第一位先取1吧,接下来我们还有6要分,还剩下两个数;第二位也取1吧,那么我们还有5要分,还剩下1个数的位置,于是我们就会发现还剩下一个数的位置,只能放5了,那么就方案数加1,返回。
这样整个搜索程序不就豁然开朗了吗?放进去三个参数,分别是上一个数的值,剩余要分的数的个数与剩下要分的数值。
此时我想你一定会有一个大大的问号吧,为什么要传上一个数的值呢?因为按照之前的栗子,为了按顺序来,是不是后面的数总会保持比前一个数大或者相等,这一点很容易理解,如果比之前的数小了,会出现重复(如1,1,5和5,1,1重复)的情况,正是如此,我们所要每一次填进去的数的范围也会得到减小,抽象的来说就是这样:前一个数<=本次所填的数<剩下要分的数值/数的个数(这是最不好理解的地方,此处的限制是为了防止前面的数过大,而后面的数连1都不能取,这样可以有效的避免了这种情况,所以在边界条件处不需要再进行判断还能不能取,因为后面的数都会满足这个关系式,所以后面的数最小都可以等于这个所填的数,所以剩下要分的数值/数的个数能保证后面的数大于或等于这个所填数),这样程序就写出来了(代码比较简单且上文有解释,就不写注释了,原谅小编的手懒):
1 #include<iostream> 2 using namespace std; 3 int n,k,a[10000],sum=0,ans; 4 void dfs(int past,int cnt,int num) 5 { 6 if(cnt==1) 7 { 8 ans++; 9 return; 10 } 11 for(int i=past;i<=num/cnt;i++) 12 dfs(i,cnt-1,num-i); 13 } 14 int main() 15 { 16 cin>>n>>k; 17 dfs(1,k,n); 18 cout<<ans; 19 return 0; 20 }