使用SVM时的注意事项:
1.支持向量机本身不能较好的支持非标准化数据。建议将数据标准化
SVM实现详细过程
https://blog.csdn.net/qq_30189255/article/details/54571370?utm_source=blogxgwz5
一、大体内容
给简短的文字实现分类。两种方法:
1.sklearn:自己提取特征采用朴素贝叶斯(NaiveBayes)、
逻辑回归(LogisticRegression)、支持向量机(SupportVectorMechine)
2.使用liblinera工具
直接把分词之后的所有词作为特征,甚至每一个字作为特征。近似于数据挖掘构造特征。
二、特征选择的方法
TF-IDF
词频-逆文档频率。TFIDF的主要思想是:如果某个词或短语在一篇文章中出现的频率TF高,并且在其他文章中很少出现,则认为此词或者短语具有很好的类别区分能力,适合用来分类。需要注意的是每个词在不同的文章中有不同的TF-IDF值,我的处理方式是每个文本中取值最大的三个词,然后把这些词做去重操作。
卡方检验CHI
在文本分类的特征选择阶段中,我们主要关心一个问题:词条t与类别C是否相互独立1)相互独立,说明词条t对类别c完全没有表征能。2)不独立,说明词条t对类别c有一定的表征能力。而这个公式就是在假设词条与类别c相互独立地情况下算出来的误差函数,误差越大说明越不独立,也就和此类别越相关。

- N:训练数据集文档总数
- A:包词词条t,同时属于类别c的文档的数量
- B:包含词条t,但是不属于类别c的文档的数量
- C:属于类别c,但是不包含词条t的文档的数量
- D:不属于类别c,同时也不包含词条t的文档的数
事非做不知道,如此小的一个知识点我实现了一遍就发现了好几个问题
- 公式还可以进一步化简,比如A+C,为属于类别c的文档数量,对于每一个词条来说都是固定的,也就没必要计算。
- 卡方的缺点是夸大了低频词的重要性,比如一个词,只在此类文章中出现了一次,跟在文章中出现了100次的词的作用性是相同的。
- 如果词在此类文章中出现的次数为0,那么卡方值会是一个固定值。
- 每个词在不同类中的卡方值是不同的,取最高的,最后一起排序去重。
三、使用sklearn中的算法实现多分类
利用上面的方法提取了10000个特征,不要利用sklearn自带的方法去将文档变成向量,那样内存会爆掉。我的方法是将特征存入列表,遍历文档的每一行,遍历词的列表,如果文本中包含这个词,则将向量值置为tfidf值或者1,前者要好一点,然后写入txt文本。在调用方法进行计算的时候,再从文本中读取向量。
分类结果
这里主要关注NB、LR和SVM的准确度和速度。
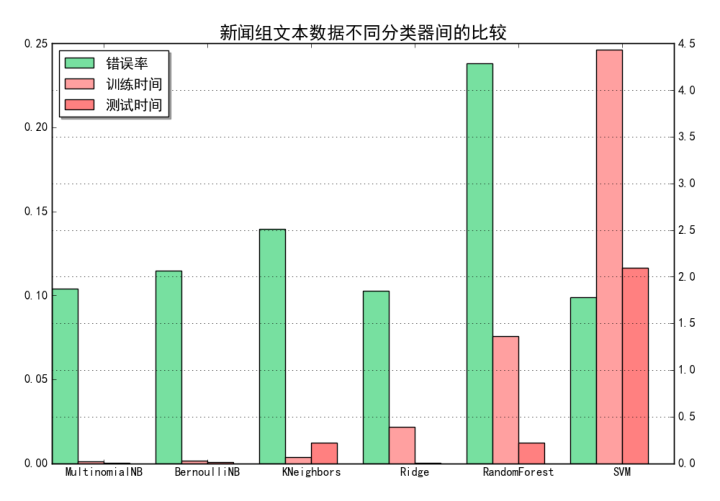
准确度:SVM>LR>NB
训练速度:NB>LR>>SVM
svm是否使用了核函数,怎么选择的
核函数是在数据线性不可分的情况下使用的,当样本的数量远大于特征的数量的时候就要考虑核函数了,本次实验样本数量1700w,特征数量1w。显然应该考虑使用核函数,但是当样本数量远大于特征数量的时候应该考虑线性核,因为非线性核的计算量太大了。
- 当数据量足够庞大时,feature足够多时,所有的分类算法最终的效果都差不多。
- 当训练集不大,feature比较多的时候,用线性的核。因为多feature的情况下就已经可以给线性的核提供不错的variance去fit训练集。
- 当训练集相对可观,而feature比较少,用非线性的核。因为需要算法提供更多的variance去fit训练集。
- feature少,训练集非常大,用线性的核。因为非线性的核需要的计算量太大了。而庞大的训练集,本身就可以给非线性的核提供很好的分类效果。
如果选用核函数,如何调参的
SVM过度依赖参数,除了过度依赖合适的核函数外,SVM还过度的依赖当前核函数下的具体参数。
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, probability=False,tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=None,random_state=None)
主要调节的参数有:C、kernel、gamma。使用交叉验证来选择最优参数。
model = svm.SVC(kernel='rbf') c_can = np.logspace(-2, 2, 10) gamma_can = np.logspace(-2, 2, 10) svc = GridSearchCV(model, param_grid={'C': c_can, 'gamma': gamma_can}, cv=5) svc.fit(x, y) print '验证参数: ', svc.best_params_
liblinear还是libsvm
在原理和实现上存在差别,libsvm是一套完整的svm实现,既包含基础的线性svm,也包含核函数方式的非线性svm;liblinear则是针对线性场景而专门实现和优化的工具包,同时支持线性svm和线性Logistic Regression模型。由于libsvm支持核函数方式实现非线性分类器,理论上,libsvm具有更强的分类能力,应该能够处理更复杂的问题。
但是,libsvm的训练速度是个很大的瓶颈,按一般经验,在样本量过万后,libsvm就比较慢了,样本量再大一个数量级,通常的机器就无法处理了;而liblinear设计初衷就是为了解决大数据量的问题,正因为只需要支持线性分类,liblinear可以采用与libsvm完全不一样的优化算法,在保持线性svm分类时类似效果的同时,大大降低了训练计算复杂度和时间消耗。
同时,在大数据背景下,线性分类和非线性分类效果差别不大,尤其是在特征维度很高而样本有限的情况下,核函数方式有可能会错误地划分类别空间,导致效果反而变差。林智仁老师也给出过很多实际例子证明,人工构造特征+线性模型的方式可以达到甚至超过kernel SVM的表现,同时大大降低训练的时间和消耗的资源。
在本次试验中文本数量是800w,特征数量5w。用libsvm时间太费时间,所以采用liblinear。
SVM如何处理多分类问题?
一般有两种做法:一种是直接法,直接在目标函数上修改,将多个分类面的参数求解合并到一个最优化问题里面。看似简单但是计算量却非常的大。
另外一种做法是间接法:对训练器进行组合。其中比较典型的有一对一,和一对多。
一对多,就是对每个类都训练出一个分类器,由svm是二分类,所以将此而分类器的两类设定为目标类为一类,其余类为另外一类。这样针对k个类可以训练出k个分类器,当有一个新的样本来的时候,用这k个分类器来测试,那个分类器的概率高,那么这个样本就属于哪一类。这种方法效果不太好,bias比较高。liblinear采用这种方法。
svm一对一法(one-vs-one),针对任意两个类训练出一个分类器,如果有k类,一共训练出C(2,k) 个分类器,这样当有一个新的样本要来的时候,用这C(2,k) 个分类器来测试,每当被判定属于某一类的时候,该类就加一,最后票数最多的类别被认定为该样本的类。libsvm采用这种方法。
Liblinear说明
考虑到训练效率,本次选用的为多线程并行版liblinear,实际为liblinear-multicore-2.1-4,首先直接给出其train命令所支持的各模式说明,各模式选择不仅与我们使用liblinear工具直接相关,也对我们理解liblinear很有帮助,下面即主要围绕这些模式展开。
ParallelLIBLINEAR is only available for -s0, 1, 2, 3, 11 now
Usage:train [options] training_set_file[model_file]
options:
-s type : set typeof solver (default 1)
formulti-class classification (dual对偶的, primal 原始的)
0 -- L2-regularized logisticregression (primal) ---逻辑回归
1 -- L2-regularized L2-losssupport vector classification (dual) ---线性svm
2 -- L2-regularized L2-loss supportvector classification (primal)--与1对应
3-- L2-regularized L1-loss support vector classification (dual)
4-- support vector classification by Crammer and Singer
5-- L1-regularized L2-loss support vector classification
6-- L1-regularized logisticregression
7-- L2-regularized logistic regression (dual)
forregression
11-- L2-regularized L2-loss support vector regression (primal)
12-- L2-regularized L2-loss support vector regression (dual)
13-- L2-regularized L1-loss support vector regression (dual)
具体solver的选择?线性svm还是logistic regression/L1正则化项还是L2正则化项
liblinear支持多种solver模式,以下直接列举liblinear支持的几种典型solver模式对应的结构风险函数(结构风险函数由损失函数和正则化项/罚项组合而成,实际即为求解结构风险函数最小值的最优化问题),以方便说明和理解。
L2-regularized L1-loss Support VectorClassification

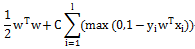
L2-regularized L2-loss Support Vector Classification
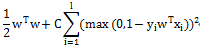
L1-regularized L2-loss Support Vector Classification
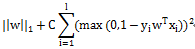
L2-regularized Logistic Regression
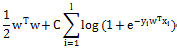
L1-regularized Logistic Regression
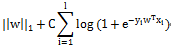
Liblinear中同时支持线性svm和logisticregression,两者最大区别即在于损失函数(loss function)不同,损失函数是用来描述预测值f(X)与实际值Y之间差别的非负实值函数,记作L(Y, f(X)),即上述公式中的项。
另一个重要选择是正则化项。正则化项是为了降低模型复杂度,提高泛化能力,避免过拟合而引入的项。当数据维度很高/样本不多的情况下,模型参数很多,模型容易变得很复杂,表面上看虽然极好地通过了所有样本点,但实际却出现了很多过拟合,此时则通过引入L1/L2正则化项来解决。
一般情况下,L1即为1范数,为绝对值之和;L2即为2范数,就是通常意义上的模。L1会趋向于产生少量的特征,而其他的特征都是0,即实现所谓的稀疏,而L2会选择更多的特征,这些特征都会接近于0。
对于solver的选择,作者的建议是:一般情况下推荐使用线性svm,其训练速度快且效果与lr接近;一般情况下推荐使用L2正则化项,L1精度相对低且训练速度也会慢一些,除非想得到一个稀疏的模型(个人注:当特征数量非常大,稀疏模型对于减少在线预测计算量比较有帮助)。
primal还是dual
primal和dual分别对应于原问题和对偶问题的求解,对结果是没有影响的,但是对偶问题可能比较慢。作者有如下建议:对于L2正则-SVM,可以先尝试用dual求解,如果非常慢,则换用primal求解。
网上另一个可参考的建议是:对于样本量不大,但是维度特别高的场景,如文本分类,更适合对偶问题求解;相反,当样本数非常多,而特征维度不高时,如果采用求解对偶问题,则由于Kernel Matrix过大,求解并不方便。反倒是求解原问题更加容易。
训练数据是否要归一化
对于这点,作者是这样建议的:在他们文档分类的应用中,归一化不但能大大减少训练时间,也能使得训练效果更好,因此我们选择对训练数据进行归一化。同时在实践中,归一化使得我们能直接对比各特征的公式权重,直观地看出哪些特征比较重要。
特征值归一化的方法
min-max标准化(Min-Max Normalization)
也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0 - 1]之间。转换函数如下:
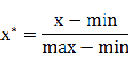
其中max为样本数据的最大值,min为样本数据的最小值。这种方法有个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义。
参考文档
https://www.cnblogs.com/XDU-Lakers/p/11698303.html
https://zhuanlan.zhihu.com/p/27939167
https://sklearn.apachecn.org/docs/0.21.3/5.html