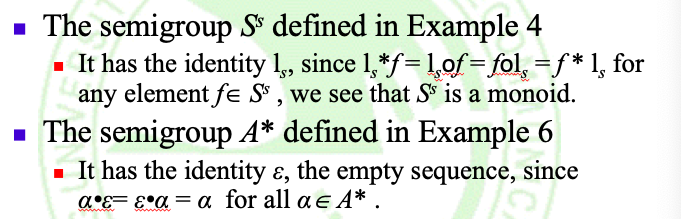10.2半群，同余关系，半群直积，商半群

半群与群(Semigroups and Groups)

半群(Semigroup)

非空集合S 和 定义在集合S上的具有结合律(封闭性显然)的二元运算(*)组成了一个半群(S, *);

• 通常记为(S, *)或者S
• a*b称为a和b的积
• 如果(*)具有交换律，那么(S, *)称为交换半群(阿贝尔半群)

如:(Z, +); (P(S), ∪)； (Z, -)...
Note:P(S)指的是S的全集，如S={1, 2, 3},那么P(S) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}

一些半群的例子:

1. 设(S^S)为所有从函数f:S -> S的集合，定义f*g = fog(即复合函数)

• *是定义在(S^S)的二元运算
• *具有结合律
• ((S^S), *)是一个半群
• 半群(S^S)不是交换群(无交换律)

2. 设(L, ≤)是一个格(lattice), 和定义在L上的二元运算*:

• a*b = a∪b
• (L, *)是一个半群

• 操作符·是指连接运算，显然其具有结合律
• 称((A^*, ·))为由A生成的自由半群(free semigroup generated by A)

定理1:

半群的卡特兰律(结合律)

单位元

单位元若存在，则必唯一

独异点(Monoid)，含幺半群

半群(S, *)中存在单位元，则称为独异点

之前例子中的半群((S^S, *), (A^*, *))等均为独异点

子半群(Subsemigroup)

T是S的子集，并且(T, *)同样满足半群定义

子独异点(Submonoid)

T是S的子集，并且(T, *)同样满足独异点定义，同时e∈T

显然，半群((S, *))本身也是S的子半群；独异点((S, *))本身也是S的子独异点；
T = {e} 一定是群((S, *))的子独异点

幂(Powers)

运算的幂通过如下定义:

生成子群和生成子独异点(由一个元素生成的子半群/子独异点)

同构映射(Isomorphism)

设有两个半群((S, *)和(T, *^{'}))
设有函数(f: S -> T)
如果

• f是从S->T的一一对应(双射)的函数
• 对任意a，b∈S, 均有(f(a*b) = f(a)*^{'}f(b))

则称f是从S到T的同构映射，简称同构

Note:如果f是从S->T的同构，即f是从S->T的一一对应的函数，那么(f^{-1})必定存在，并且(f^{-1})是从T->S的一一对应的函数(并且一定是同构，下证)

构造同构/判断是否为同构的一般步骤:

1. (构造或直接给出)构造一个函数(f:S -> T),使得f的定义域Dom(f) = S;
2. 证明f是单射(one-to-one)的，可用反证法
3. 证明f是满射(onto)的 --> 故而是双射的
4. 证明(f(a*b) = f(a)*^{'}f(b))
   EXP:证明(Z, +) -> (T, +)，其中Z是整数集，T是偶数集

定理2:

如果S和T是独异点，且幺元分别为(e，e^{'}),并且存在(f:S->T)是从S到T的同构映射，那么:

• (f(e) = e^{'})

Note:显然，如果((S, *))有独异点，但((T, *^{'}))没有独异点，那么必定不存在从S->T的同构(常用于证明不存在同构)

同态映射(Homomorphism)

设有两个半群((S, *)和(T, *^{'}))
设有函数(f: S -> T)
如果

• 对任意a，b∈S, 均有(f(a*b) = f(a)*^{'}f(b))
  则称f是从S到T的同态映射，简称同态
  

Note:同构和同态均满足：像点的乘积等于乘积的像点

定理3:

如果S和T是独异点，且幺元分别为(e，e^{'}),并且存在(f:S->T)是从S到T的满同态映射，那么:

• (f(e) = e^{'})

f必须是满同态才行，因为假如T中有个元素a没被映射，你凭啥说e'a＝a?

定理4:

如果S和T是半群,并且存在(f:S->T)是从S到T的同态映射，并且假设(S^{'})是(S, *)的子半群，那么:

• (S^{'}的像f(S^{'})也是(T, *^{'}))的子半群

证明如下:

定理5:

如果S是交换半群,T是半群,并且存在(f:S->T)是从S到T的满同态映射，那么:

• ((T, *^{'}))也是交换半群

这里同样要求满同态
证明如下:

半群直积和商半群(Products and Quotients of Semigroups)

定理1:

两个半群的笛卡尔乘积也是半群

((S, *)和(T, *^{'})是半群，它们的笛卡尔乘积(S×T, *^{''})也是半群，其中二元运算*^{''}定义为: (s_1, t_1)*^{''}(s_2, t_2) = (s_1*s_2, t_1*^{'}t_2))

同样的，两个独异点的笛卡尔乘积也是独异点且其幺元为((e_S, e_T))

同余关系(Congruence relation)

定义在群((S, *))上的等价关系R，如果满足:

任意a R a' 并且 b R b' ==> ((a*b) R (a'*b'))

那么我们说R是同余关系

Note:在S中等价于一个关系的所有元素则被划分为一个等价类,对于代数结构(群)也是如此

• 我们让[a] = R(a)来表示包含元素a的等价类
• S/R表示所有等价类的集合

定理2:

令R是定义在半群(S, *)上的同余关系R
下定义关系 口 :

其中, 口([a], [b]) = [a] 口 [b] = [a*b],显然 口 是从(S/R×S/R -> S/R) 的一个函数

(S/R， 口)是一个半群,并且S/R称为商半群(quotient semigroup或者factor semigroup)
因为 口 对于S/R是一个二元运算并且满足结合律

推论:

如果(S, *)是独异点，那么(S/R, 口)也是独异点(商独异点？)，其幺元为[e]

定理3:

令R为定义在半群(S, *)上的同余关系，(S/R 口)是相应的商半群，那么下面这个函数:

是一个满同态(onto homomorphism)，也称为自然同态(natural homomorphism)
证明如下:

同态基本定理(Fundamental Homomorphism Theorem)

定理内容:

设f:S -> T是半群((S, *))到半群(T, *')的一个同态，设R是定义在S上的一个关系且定义为对于S中的任意a和b，a R b 当且仅当 f(a) = f(b),那么:

• (a). R是一个同余关系
• (b). (T, *')和商半群(S/R, 口)是同构的

1.证明R是同余关系(congruence relation)

2.定义并证明一个从S/R到T的双射函数

3.证明该双射函数是同态 -》 是同构