【ybt金牌导航8-1-4】【luogu P4151】路径最大异或和 / 最大XOR和路径

路径最大异或和 / 最大XOR和路径

题目链接：ybt金牌导航8-1-4 / luogu P4151

题目大意

给你一个无向图，边有边权，要你找一条从 1 到 n 的路径，使得路径上经过的边边权异或起来最大。
如果重复经过边，那边权要异或多次。

思路

首先我们想想没有环怎么搞。
那容易 DP 一下得到 (dis_i)（从 (1) 到 (i) 的路径异或和），那答案就是 (dis_n)。

但你想到它有环。
那假设这些环都不在 (1) 到 (n) 的最短路径上。
那我们就可以选择专门去经过这个环或不经过，根据异或有贡献分别是环边的异或和以及 (0)。

那如果在路径上呢？

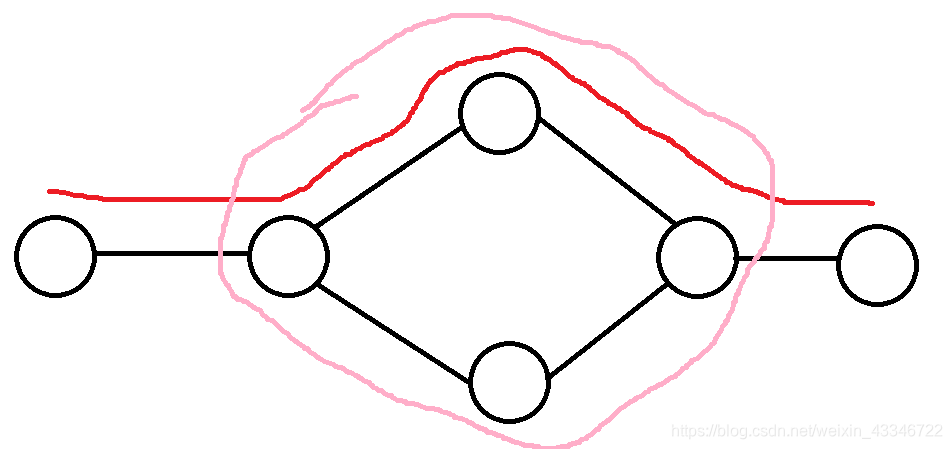
红色是你选的一个路径，然后粉色是在路径上的一个环。
那你把它们异或起来，你就发现，它就变成了这个：

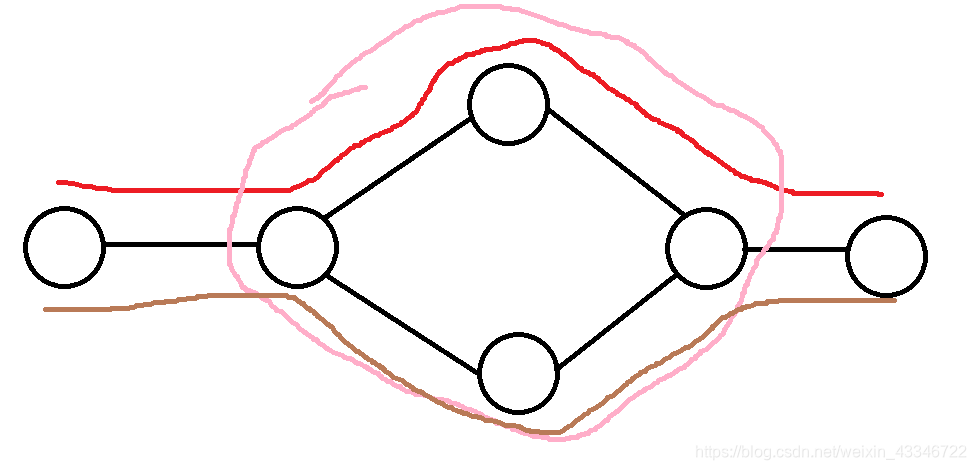
棕色的那个，就是另一条路径了，那我们可以根据要不要一个这个环来改变要走的路径。

那接着有人会问，可能两个小环会组成大环，你要把所有的环都找出来，不也会超时吗？
那我们再画图来看：

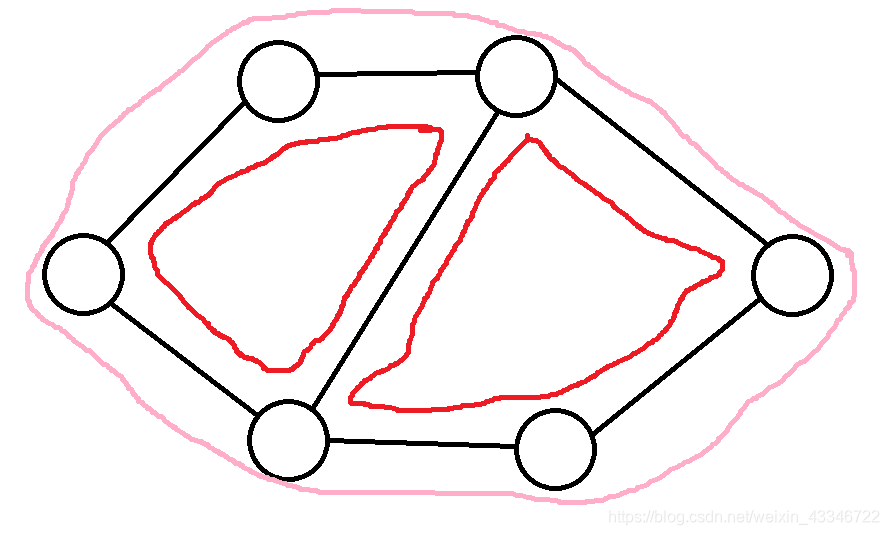
红色是两个小环，粉色是大环。
那你发现，你把两个小环异或起来，就是你要的大环了。
那我们其实可以通过小环的组合异或，得到所有的环。

那问题就变成了给你一堆数，有一个数一定要选（你找的随便一个从 (1) 到 (n) 的路径），其它的任选一些（小环），要选出的数的异或值最大。
那就是线性基搞搞就好了。

代码

#include<cstdio>
#define ll long long

using namespace std;

struct node {
	ll x;
	int to, nxt;
}e[200001];
int n, m, le[50001], x, y, KK;
ll z, dis[50001], p[101];
bool in[50001];

void add(int x, int y, ll z) {
	e[++KK] = (node){z, y, le[x]}; le[x] = KK;
	e[++KK] = (node){z, x, le[y]}; le[y] = KK;
}

//线性基
void xxj_add(ll x) {
	for (int i = 60; i >= 0; i--)
		if ((x >> i) & 1) {
			if (!p[i]) {
				p[i] = x;
				break;
			}
			x ^= p[i];
		}
}

//dfs
void dfs(int now, int father) {
	in[now] = 1;
	for (int i = le[now]; i; i = e[i].nxt)
		if (!in[e[i].to]) {//正常跑
			dis[e[i].to] = dis[now] ^ e[i].x;
			dfs(e[i].to, now);
		}
		else {//形成了环
			xxj_add(dis[now] ^ dis[e[i].to] ^ e[i].x);
		}
}

ll get_max(ll re) {//线性基求最大值
	for (int i = 60; i >= 0; i--)
		if (!((re >> i) & 1))
			if (p[i])
				re ^= p[i];
	return re;
}

int main() {
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= m; i++) {
		scanf("%d %d %lld", &x, &y, &z);
		add(x, y, z);
	}
	
	dfs(1, 0);
	
	printf("%lld", get_max(dis[n]));
	
	return 0;
}