软件测试技术 hw3

作业题目：教材49页第7题a到d，并基于Junit及Eclemma实现一个主路径覆盖的测试
一、Use the following method printPrimes() for questions a-f below

1./** *****************************************************
2. * Finds and prints n prime integers
3. * Jeff Offutt, Spring 2003
4. ********************************************************* */
5. private static void printPrimes (int n)
6. {
7. int curPrime; // Value currently considered for primeness
8. int numPrimes; // Number of primes found so far.
9. boolean isPrime; // Is curPrime prime?
10. int [] primes = new int [MAXPRIMES]; // The list of prime numbers.
11.
12. // Initialize 2 into the list of primes.
13. primes [0] = 2;
14. numPrimes = 1;
15. curPrime = 2;
16. while (numPrimes < n)
17. {
18. curPrime++; // next number to consider ...
19. isPrime = true;
20. for (int i = 0; i <= numPrimes-1; i++)
21. { // for each previous prime.
22. if (isDivisible (primes[i], curPrime))
23. { // Found a divisor, curPrime is not prime.
24. isPrime = false;
25. break; // out of loop through primes.
26. }
27. }
28. if (isPrime)
29. { // save it!
30. primes[numPrimes] = curPrime;
31. numPrimes++;
32. }
33. } // End while
34.
35. // Print all the primes out.
36. for (int i = 0; i <= numPrimes-1; i++)
37. {
38. System.out.println ("Prime: " + primes[i]);
39. }
40. } // end printPrime

a.画出控制流图
解答：

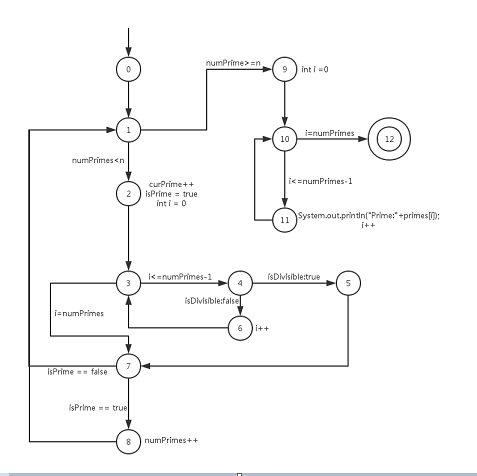
b.设计一个t2=(n=5)比t1=(n=3)容易发现发现的错误

解答：数组越界

c.写一个测试用例，使相应的测试路径访问连接while语句开始到fot语句得边，而不用通过while的循环体

解答：t：n=1

d.例举每个节点覆盖，边覆盖和主路径覆盖的TR

解答：

节点覆盖需求：{1,2,3,4,5,6,7,8,9,10,11,12,13}

边覆盖需求：{(1,2),(2,3),(2,10),(3,4),(4,5),(4,8),(5,6),(5,7),(6,8),(7,4),(8,2),(8,9),(9,2),(10,11),(11,12),(11,13),(12,11)}

主路径覆盖需求：

{

(4,5,6,4)

(6,4,5,6)

(5,6,4,5)

(5,6,4,,8,,2,3)

(5,6,4,8,2,10,11,12,11)

(5,6,4,8,2,10,11,13)

(3,4,5,7,8,9,2,3)

(3,4,5,7,8,2,3)

(3,4,8,9,2,3)

(3,4,8,2,3)

(3,4,5,7,8,9,2,10,11,12)

(3,4,5,7,8,9,2,10,11,13)

(3,4,5,7,8,2,10,11,12)

(3,4,5,7,8,2,10,11,13)

(3,4,8,2,10,11,13)

(3,4,8,2,10,11,12)

(4,5,7,8,9,2,3,4)

(4,5,7,8,2,3,4)

(4,8,9,2,3,4)

(4,8,2,3,4)

(1,2,3,4,8)

(1,2,3,4,5,6)

(1,2,3,4,5,7,8,9)

(1,2,10,11,12)

(1,2,10,11,13)

(11,12,11)

(12,11,12)

(12,11,13)

}

二.实现一个主路径覆盖的测试

使用第一次上机判断三角形的程序：

package zjz;

public class triangle {
    
    private static int result=0;
    public void TypeOfTriangle(int a,int b,int c) {
        if(a + b <= c || a + c <= b || b+ c <= a && a<=0 && b <= 0 && c <=0){
            result = 1; //不是三角形
            
            if(a == b && a == c)
                result = 2;//等腰
            
            if(a == b || b == c || a == c)
                result = 3;//等边
            else
                result = 4;//普通
        }
        
    }
    
    public int getResult(){
        return result;
    }
       public void clear(){
         result = 0;    
}

测试类用例：

package zjz;
import static org.junit.Assert.*;
import org.junit.Test;
public class TestCalculator {
    private static Calculator cal = new Calculator();
    @Test
    public void testTriangle(){
        
    cal.triangle(2, 2, 2);
    assertEquals(3, cal.getReuslt());//等边三角形
    cal.triangle(3, 3, 5);
    assertEquals(2, cal.getReuslt());//等腰三角形
    cal.triangle(3, 4, 5);
    assertEquals(1, cal.getReuslt());//普通三角形
    cal.triangle(1, 2, 3);
    assertEquals(0, cal.getReuslt());//不能构成三角形
    }

}

覆盖率截图：