2021-08-03训练记录
Magic Line

样例输入
1
4
0 1
-1 0
1 0
0 -1
样例输出
-1 999000000 1 -999000001
这道题是2019年牛客多校的题,稍微画下图然后就很轻松地能够区分开来了,本题为特判,做起来可能比较轻松
string s;
struct node {
int x, y;
bool friend operator<(node a, node b){
if (a.x != b.x) return a.x < b.x;
return a.y < b.y;
}
} a[maxn];
int main()
{
int _ = read;
while (_--) {
int n = read;
for (int i = 1; i <= n; i++) a[i].x = read, a[i].y = read;
sort(a + 1, a + 1 + n);
int lim = 100000000;
int a1 = a[n / 2].x;
int a2 = a[n / 2 + 1].x;
if (a1 == a2) {
printf("%d %d %d %d
", a1 - 10, lim, a1 + 10, (a[n / 2].y + a[n / 2 + 1].y) - 1 * lim);
}else{
printf("%d %d %d %d
", a[n / 2].x, lim, a[n / 2 + 1].x, -1 * lim);
}
}
return 0;
}
这么做也是可以的:
struct node{
int x;int y;
}s[100005];
bool cmp(node d1,node d2)
{
if(d1.x==d2.x)return d1.y<d2.y;
return d1.x<d2.x;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&s[i].x,&s[i].y);
sort(s+1,s+1+n,cmp);
printf("%d %d %d %d
",s[n/2].x-1,s[n/2].y+999000001,s[n/2].x+1,s[n/2].y-999000000);
}
}
String Invasion
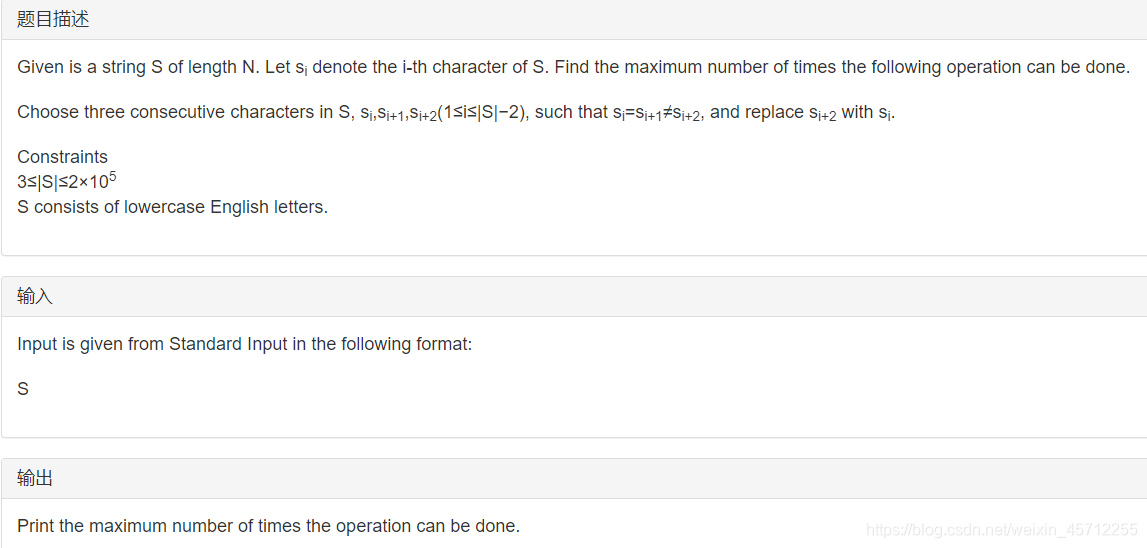
样例输入
【样例1】
accept
【样例2】
atcoder
【样例3】
anerroroccurred
样例输出
【样例1】
3
【样例2】
0
【样例3】
16
提示
样例1解释
We can do the operation three times, as follows:
do it with i=2, changing the string to acccpt;
do it with i=3, changing the string to acccct;
do it with i=4, changing the string to accccc.
从后向前推就好了,队友代码:
int n,cnt;
ll sum;
map<char,int>mp;
int main(){
string s; cin>>s; n=s.size();
for(int i=n-1;i>=0;i--){
mp[s[i]]++;
if(i+2<n&&s[i]==s[i+1]&&s[i+1]!=s[i+2]){
sum+=0ll+n-i-mp[s[i]];
mp.clear();
mp[s[i]]=n-i;
}
}
out(sum);
}
我的思路是从前往后进行贪心,找相连的两个相同字母,然后重新存储起来,从后向前进行推,要按注意区间内是否有不用替换的操作,比如aabbcdebrfbcc 这种,前面的bb到cc之间有两个b的贡献要减去
对于上述字符串来讲,贡献就是cc后面的部分减去cc后面中c的数量(本部分为0),bb != cc所以说bb以后的贡献就是总长度 - aabb的长度 - 后面两个b的贡献.
注意,如果是这种aabcdaacd 在前面的aa位置贡献就是后面的aa中第一个a位置 - 前面的aa中第二个a的位置 - 1
string s;
struct node {
char c;
int p1, p2;
} a[maxn];
int main()
{
cin >> s;
int n = s.size(), cnt = 0;
s = "#" + s;
for (int i = n; i >= 1; i--) {
if (s[i] == s[i - 1]) {
++cnt;
++a[cnt].c = s[i];
a[cnt].p1 = i - 1;
a[cnt].p2 = i;
while (s[i - 1] == a[cnt].c) --i;
}
}
ll ans = 0;
stack<node> st;
for (int i = 1; i <= cnt; i++) {
st.push(a[i]);
}
for (int i = 1; i <= cnt; i++) {
a[i] = st.top();
st.pop();
}
if (cnt) ans = n - a[cnt].p2;
// cout << cnt << endl;
// for (int i = 1; i <= cnt; i++) {
// cout << a[i].c << " " << a[i].p1 << " " << a[i].p2 << endl;
// }
// debug(ans);
for (int i = cnt - 1; i >= 1; i--) {
if (a[i].c != a[i + 1].c) {
ans += n - a[i].p2;
}else{
ans += a[i + 1].p1 - a[i].p2 - 1;
}
}
// cout << ans << endl;
for (int i = cnt - 1; i >= 1; i--) {
// cout << a[i].p2 << " " << a[i + 1].p1 << endl;
for (int j = a[i].p2 + 1; j < a[i + 1].p1; j++) {
if (s[j] == a[i].c) --ans;
}
}
for (int i = a[cnt].p2 + 1; i <= n; i++) {
if (s[i] == a[cnt].c) ans--;
}
cout << ans << endl;
return 0;
}
/**
atcoder
anerroroccurred
**/
/**************************************************************
Problem: 18564
Language: C++
Result: 正确
Time:21 ms
Memory:38520 kb
****************************************************************/
ABC
Given a positive integer K, find the number of triples of positive integers (A,B,C) such that ABC≤K. Two triples that only differ in the order of numbers are also distinguished.
Constraints
1≤K≤2×105
K is an integer.
输入
Input is given from Standard Input in the following format:
K
输出
Print the number of triples of positive integers (A,B,C) such that ABC≤K.
样例输入 Copy
【样例1】
2
【样例2】
10
【样例3】
31415
样例输出 Copy
【样例1】
4
【样例2】
53
【样例3】
1937281
提示
样例1解释
We have the following triples: (1,1,1),(1,1,2),(1,2,1),(2,1,1).
枚举前两个元素 i , j ,第三个元素的范围就是 [ 1 , K / i / j ], 加上个数 K / i / j
int main()
{
ll ans = 0;
n = read;
for (int i = 1; i <= n; i++) {
for (int j = 1; i * j <= n; j++) {
ans += n / i / j;
}
}
cout << ans;
return 0;
}
小biu放牛
题目描述
小Biu最喜欢的活动就是放牛,但是由于他比较懒,所以他喜欢把牛拴在木桩上,小Biu有N头牛和N个木桩,农场的总长度为M,每头牛的身长为2*x,N个木桩为位置分别为p[i],现在小Biu想把所有的牛排成一排,并且每只牛都必须栓在木桩上,小Biu一般选择在牛身的中间栓绳子,所以可以认为绳子的位置距离牛头和牛尾的距离都是x。而且一个木桩只能栓一个牛,牛和牛的身体间不能重叠,现在小Biu想知道,如果他想把这N只牛拴在这N个木桩上,需要的所有绳子中的最长的那个绳子长度最小为多少,如果农场不能放下所有的牛,输出-1。
输入
第1行:3个数N X M,中间用空格分隔(1 <= N <= 50000, 1 <= X <= 10^9, 1 <= M <= 10^9)。
第2 - N + 1行:每行1个数Pi,对应木桩的位置(0 <= Pi <= Pi+1 <= M),并且给出的数据是有序的。
输出
输出最长绳子的最小值。如果码头排不下所有船则输出-1。
样例输入 Copy
3 2 16
1
3
14
样例输出 Copy
3
提示
N = 3, X = 2, M = 16。三个木桩的位置为:1 3 14。牛的身长为2*X = 4。你可以将三头牛放在2 6 14(指的是牛身中间所处的位置),这样牛和牛之间既没有重叠,并且所用的最长的绳子最短,长度为3,即第2头牛到第二根木桩的距离。
对于35%的数据,n<=10
对于70%的数据,n<=10000
对于100%的数据,n<=50000
ll a[maxn], b[maxn];
ll n, m, x;
bool judge(int len)
{
///sum > m return 0;
a[1] = max(a[1] - len, x);
if (a[1] - b[1] > len) return false;
for (int i = 2; i <= n; i++) {
a[i] = b[i];
if (a[i - 1] + 2 * x - a[i] > len) return false;
if (a[i] - a[i - 1] >= 2 * x) a[i] = max(a[i - 1] + 2 * x, a[i] - len);
else a[i] = a[i - 1] + 2 * x;
if (a[i] + x > m) return false;
}
return true;
}
int main()
{
n = read, x = read, m = read;
for (int i = 1; i <= n; i++) a[i] = b[i] = read;
int l = 0, r = mod;
int ans = -1;///-1-1-1
while (l < r) {
int md = (l + r) >> 1;
if (judge(md)) {
ans = md;
r = md;
// puts("in");
}else{
l = md + 1;
}
a[1] = b[1];
// debug(md);
}
cout << ans << endl;
return 0;
}
小A的游戏
题目描述
小A在和小B玩一个游戏,小A有一个字符串S,现在小A删除了其中K个字符,给出删除前的字符串S,和删除后的字符串S’,现在小A想知道,是否无论怎样删除,小B都能猜中他删除了哪些位置上的字母。
若一定,输出 Certain ,否则输出 Uncertain 。
输入
第一行一个正整数t,表示数据组数。
第二行一个字符串表示 s 。
第三行一个正整数表示 K 。1≤K≤|s|≤100 ,s 仅包含小写字母。
输出
对于每组数据,输出一行一个字符串。
若一定,输出 Certain ,否则输出 Uncertain 。
样例输入 Copy
1
snuke
2
样例输出 Copy
Certain
提示
例如如果小a删去s,e,则她告诉你"nuk",那么小b可以确定删去的是原串的第1个字符和第5个字符。
无论小a删去哪两个字符,小b都一定可以确定其在原串的位置。
对于50%的数据,t<=10,k<=n<=10
对于70%的数据,t<=10,k<=n<=20
对于100%的数据,t<=10,k<=n<=100
int a[12][5]; int main() { int _ = read; while (_--) { map<char, ll> mp; string s; cin >> s; int siz = s.size(); ll mini = inf; for (ll i = 0; i < siz; i++) { if (mp[s[i]]) mini = min(mini, i - mp[s[i]]); mp[s[i]] = i + 1; } int cnt = read; if (cnt == siz) cnt = 0; if (cnt <= mini) puts("Certain"); else{ puts("Uncertain"); } } return 0; } /** **/ /************************************************************** Problem: 14049 Language: C++ Result: 正确 Time:2 ms Memory:2044 kb ****************************************************************/
A^ B ^ C
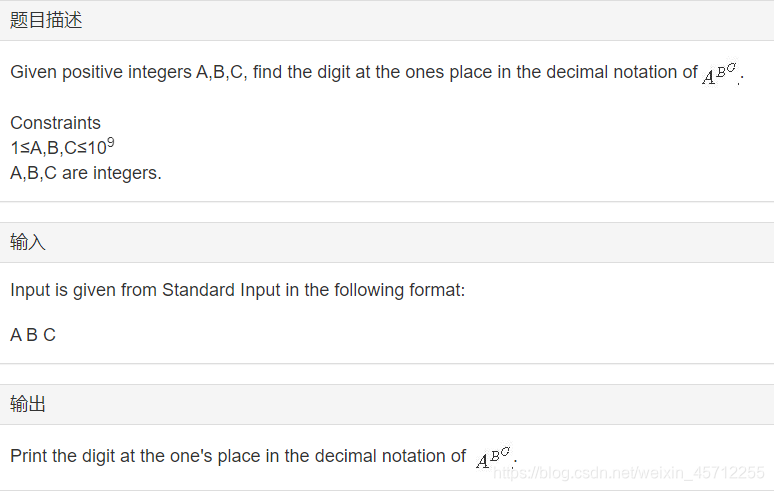
样例输入 Copy
【样例1】
4 3 2
【样例2】
1 2 3
【样例3】
3141592 6535897 9323846
样例输出 Copy
【样例1】
4
【样例2】
1
【样例3】
2

规律题,完全可以不用什么欧拉降幂之类的
