后缀数组是处理字符串的有力工具。————罗穗骞
·前面的言
在后缀树,后缀自动机以及后缀数组三者中似懂非懂地抉择之后,综合代码量和实用性方面的考虑,你选择了学习后缀数组。本文会像往常一样,以更加朴素和便于理解的方式来献出大米饼自己对于后缀数组的理解。
·LCP——一个问题的引入
LCP(Longest Common Prefix)即最长公共前缀。下面给出这样一个问题:输入一个字符串,有许多询问,每次询问(a,b)表示要求出该串长度为a的后缀和长度为b的后缀的LCP。两种方法:
①暴力:对于每个询问,扫描一遍这两个后缀,得出LCP的值。O(n)
②后缀数组:对于每个询问,进行______操作,得出LCP的值。O(logn)
为了解决这个问题,接下来既是对后缀数组的讲解,同时也是对这个问题的解法的探寻。
·对后缀排序——后缀数组的构建
接触新的算法一定会想知道这个新玩意儿长啥样。我们在这里可以举一个简单的例子来为一个字符串量身定制一款后缀数组:
[例]你获得了字符串S=" a b c a c a b c " ,看下面啦:
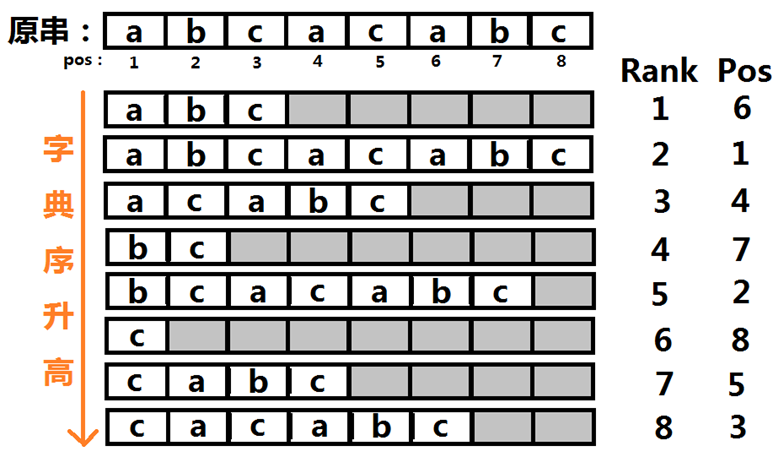
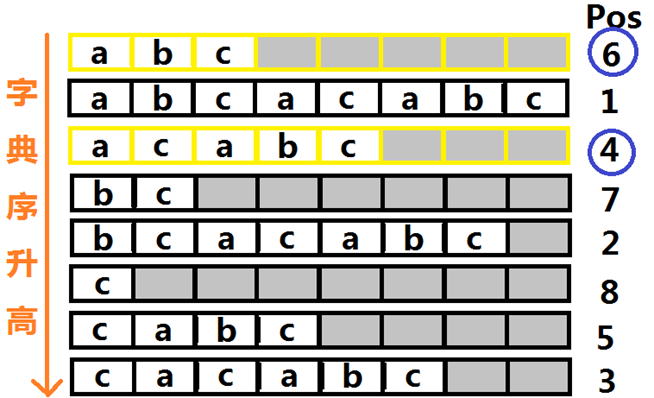
首先,我们给每个后缀编号,编号方式为这个后缀的左端点下标(例如长度为2的那个后缀"bc"的编号就是7)。然后可以看下图了:
你看见后缀数组了吗?让我们来一一解释。上图中将原串的每个后缀取出来按照字典序从小到大排序得到图片的下面部分。然后我们可以发现对于每个后缀,在其右边标注了两个元素:Rank和Pos。Rank其实呢就是指它的字典序是第几小(在排序中排第几),至于Pos,正是上文提到的每个后缀的编号。按照排序顺序,将编号存入一个数组sa[],sa[i]即可表示字典序第i小的后缀的编号——你获得了后缀数组(sa:Suffix Array!)。
不过呢后缀数组是放在一个套餐里面售卖的,和它捆绑卖出的还有这些作用不可小觑的数组:rank[],height[]。
rank[]在此不同于图片中的Rank。rank[]其实是sa[]的互逆数组,让我们比较一下定义就知道了:
—————①sa[i]:表示第i小的后缀的编号
—————②rank[i]:表示编号i的后缀排第几
height[]便是一个很大的特色了。它的定义是很奇妙的:heigt[i]表示第i小的后缀和第(i-1)小的后缀的LCP长度。这里会让人感觉height[]的构造一定慢乎乎的(比如暴力预处理),但事实是在后文中将O(n)得出所有的height[i]。
·解决LCP问题——后缀数组的效果展示
回到最初的问题,询问任意两个后缀的LCP长度使用后缀数组应该怎么做呢?如果询问的两个后缀排名是相邻的,那么答案就是height[i]。但要是排名不相邻呢?如下图,现在询问编号为4和6的后缀的LCP长度:
我们发现询问4,6的LCP其实等于询问询问6,1的LCP和1,4的LCP的最小值。归纳地说,询问编号为i,j的后缀的LCP,其实就是在询问排序后的后缀序列里排在前面的询问串到排在后面的询问串之间的区间里的所有height[]的最小值。(别忘了height的定义!)画个图加深理解(红色为询问的两后缀):
这样的好处是使得每个询问转化为了询问区间最小值,那么写个RMQ之类的就可以快速维护了。虽然还没讲到sa[],height[]的构建方法,但是可以先预告一下以便体会这种方法的优越性:sa[]需要O(nlogn)时间构造,height[]需要O(n)时间构造,加上RMQ,该方法时间复杂度为O(nlogn),完美胜过暴力。到此一个小小提醒是一定要分清排名和编号,这对于理解非常重要。
·基数排序——O(nlogn)预处理sa数组
虽然只是一个预处理,但是很重要而且相对来说需要理解的细节很多(刘汝佳在书中表示:"代码实现中有很多的细节……")。
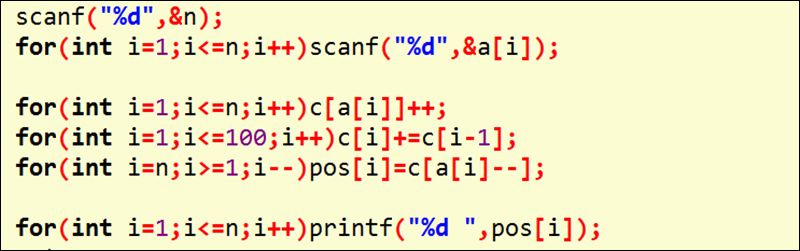
基数排序类似于桶排序,其方法是用c[i]表示为i的数的个数,将c[i]累加,即:c[i]+=c[i-1],然后将序列倒序枚举,此时的c[a[j]]表示的正是该数从小到大排第几,随即c[a[j]]--。例如这样一个问题:输入一个长度为n的序列,元素大小不超过100且为正整数,按照输入顺序输出每个元素按从小到大排序后的位置。给出该问题的代码,目的是快速理解基数排序:
值得注意的是,预处理后缀数组(sa数组),不仅要用到基数排序,还需要用到另外两个思想:
思想一:并不需要每一位比较完。实际上两个后缀从第一位开始比较大小,只要到达了第一个不相同的一位,就可以判断谁大谁小了。因此,预处理的宗旨是:先把每个后缀只比较第一位,然后得出排名,如果排名有相同(即第一位相同),那么又比较每个后缀的第二位,直到没有相同排名,就直接跳出程序,因为此时已经可以分辨所有后缀的大小关系了。
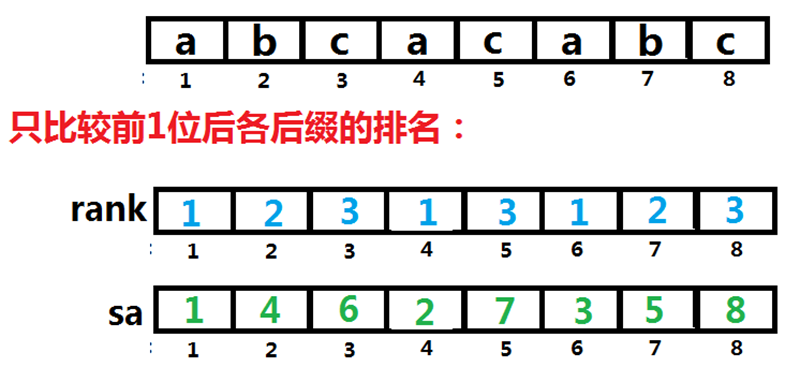
思想二:思想一结尾处提到的方法可以利用倍增的思想优化。即所有后缀先比较前1位,如果排名有相同就比较前2位,然后前4位,前8位……此处方法成立的原因原来的比较长度可以拼成二倍的长度为新的比较所用。那么值得注意的是,这样做每一次相当于双关键字排序,下面给出样例数组的部分排序:
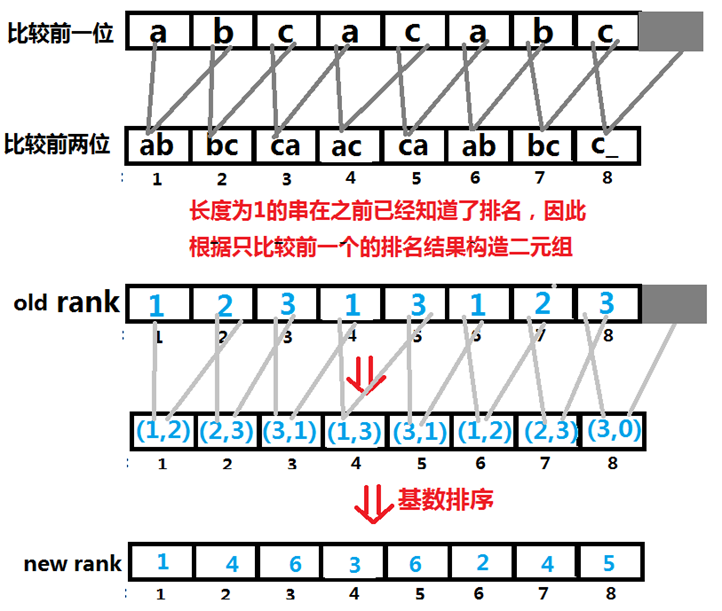
你可以发现图中的sa数组是假的,原因是sa[1],sa[2],sa[3]里面三个后缀排名应该是相同的而不是1,2,3。但这只是临时的,别忘了比较的跳出条件是没有相同排名,即rank中没有相同元素。接下来要让预处理跑起来,上述图片只是初始化。因为我们发现只比较第一位不足以区分大小,因此比较前2位:
看上去整个预处理可以直接在rank上完成。但是双关键字的基数排序怎么写呢?妙招:我们知道,对于双关键字排序,可以将数列按照优先级较低关键字排序,然后再按第一关键字排序。所以,此处我们想办法先让第二关键字(即图中的每个括号第二位)有序,然后进行第一关键字的基数排序。
使得第二关键字有序,我们可以直接使用当前假的sa[],因为sa内部是有序的,只需要按照sa的下标顺序将对应编号的后缀放入数组就可以保证第二关键字有序了,最后对这个数组进行第一关键字排序。排序结束后下标就是新的 rank的值。此处一定要分清rank和sa!(本段应该是最难理解的一段,接下来的代码解释中还会换种方式讲解)
每一次比较结束后,我们就可以推出新的sa和rank。由于每一次比较的前k为是一个倍增,因此算法此处时间复杂度为O(nlogn)。
这里是细节较多的预处理sa的代码(先试着看懂,不懂的小段接下来会分析)
其中s[i]表示原串,k表示当前比较前2*k位,y[]就是上文提到的用来双关键字排序的数组,最终它会更新x[],x[]就是临时的rank数组。(但是为了方便最后一段会直接交换x,y,意义也随之交换)
一步一步分析:
while循环之外就是初始化,表示只比较第一位的情况下各后缀的排名以及对应的sa[]。
while循环之内:
①利用sa[]按照第二关键字排序:
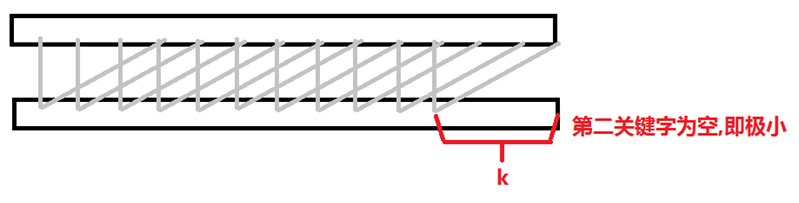
第一行的意义是新形成的rank数组在区间[n-k+1,n]之间的部分是没有第二关键字的,即(key1,0),原因是现在要比较2*k位如图:
第二行的意义就是利用sa数组本来的顺序来保证第二关键字有序。注意理解为什么是sa[i]-k,表示k拿来拼成2*k,就像图中一样每个二元组的第二关键字来源都是来自oldrank数组的该位置+k,所以在用sa的时候要减去k来获得第二关键字所在二元组的位置。
②将已经第二关键字有序的y[]数组进行第一关键字基数排序:
前面三行都是标准的基数排序。最后一行得出了新的sa数组。
③按照新的sa的顺序更新x(即更新rank)
注意此处y实际上存的是old x[](old rank),第四排的判断条件的意思是如果当前排序后相邻二元组双关键字相同那么排名是一样的,p就不能++。p统计出来就是不同排名的个数,当不同排名个数等于n的时候,while就可以跳出了。
总结来说,该部分复杂在sa和rank对预处理的同时作用,因为两个数组本身互逆,所以涉及到数组下标顺序等问题,容易搞混。
·发现规律——O(n)预处理height数组
在经历了上文基数排序预处理的大杂烩后,height数组的线性递推显得很清新美妙。先说结论:如果按照后缀编号i的顺序枚举height[rank[i]],那么可以做到线性时间复杂度预处理。基于这样一个结论(注意rank的定义):
height[rank[i]]>=height[rank[i-1]]-1
证明如下:
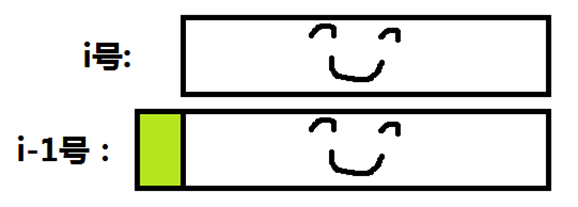
因为编号为i的后缀比编号为(i-1)的后缀少一位元素,如图:
考虑在按字典序排序后的顺序下,这个i-1号和排在它前面的那一个串x的LCP值为height[rank[i-1]],然后我们将x的第一个元素砍掉,也就是得到了另一个后缀,那么:由于这个后缀和i-1号从第二位开始有(height[rank[i-1]]-1)长度相同,i-1号又只与i号差第一个元素,所以这个后缀一定和i的LCP正是等于(height[rank[i-1]]-1),所以height[rank[i]]是不会小于这个值的。
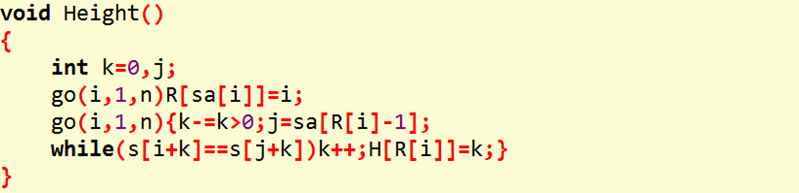
这部分代码迫不及待地出来了:(height简写为H,rank简写为R)
[Final Code](base on HDU 1403):
#include<stdio.h> #include<cstring> #include<algorithm> #define go(i,a,b) for(int i=a;i<=b;i++) #define ro(i,a,b) for(int i=a;i>=b;i--) using namespace std;const int N=200003; char s[N];int c[N],m,n,t1[N],t2[N],sa[N],H[N],R[N],mid; void SA() { int *x=t1,*y=t2,k=1,p=0; go(i,1,m)c[i]=0;go(i,1,n)c[x[i]=s[i]]++; go(i,2,m)c[i]+=c[i-1];ro(i,n,1)sa[c[x[i]]--]=i; while(k<=n&&p<n&&1+(p=0)) { go(i,n-k+1,n)y[++p]=i; go(i,1,n)if(sa[i]>k)y[++p]=sa[i]-k; go(i,1,m)c[i]=0;go(i,1,n)c[x[y[i]]]++; go(i,2,m)c[i]+=c[i-1];ro(i,n,1)sa[c[x[y[i]]]--]=y[i];swap(x,y);p=x[sa[1]]=1; go(i,2,n)x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p:++p;m=p;k<<=1; } } void Height() { int k=0,j; go(i,1,n)R[sa[i]]=i; go(i,1,n){k-=k>0;j=sa[R[i]-1]; while(s[i+k]==s[j+k])k++;H[R[i]]=k;} } int main() { while(~scanf("%s",s+1)) { m=400;n=strlen(s+1);s[mid=n+1]='a'-1; scanf("%s",s+n+2);n=strlen(s+1);SA();Height();int Max=0; go(i,2,n)if(H[i]>Max&&(mid-sa[i])*(mid-sa[i-1])<0)Max=H[i]; printf("%d ",Max); } return 0; }//Paul_Guderian
大米飘香的总结:
本文重在探寻一种很好的理解后缀数组构造的全过程的方式。后缀数组可以替代后缀树,也可以在大多题目中替代后缀自动机,因此为相关问题的首选方法。另外,对于预处理sa数组,可以用DC3算法O(n)获取,但是常数,空间以及编码复杂度变大。此文并未谈及一些后缀数组经典例题,大米饼建议参看罗穗骞的论文上的经典题目来弥补这一缺陷。真诚地祝愿来此浏览的Oier能够有所收获,一步一步追逐梦想,踏踏实实走向高峰。
却在北京上海广州深圳某天夜半忽然醒来,像被命运叫醒了,
它说你不能就这样过完一生……————————《你曾是少年》