最小生成树 & 洛谷P3366【模板】最小生成树 & 洛谷P2820 局域网

嗯...

理解生成树的概念：

在一幅图中将所有n个点连接起来的n-1条边所形成的树。

最小生成树：

边权之和最小的生成树。

最小瓶颈生成树：

对于带权图，最大权值最小的生成树。

如何操作？

1.Prim算法（O（mlogn））

2.Kruskal算法（O（mlogn））

算法流程：

Prim算法：（思想类似dijkstra）

　　随意选取一个点作为已访问集合的第一个点，并将所有相连的边加入堆中
　　从堆中找到最小的连接集合内和集合外点的边，将边加入最小生成树中
　　将集合外点标记为已访问，并将相连边加入堆
　　重复以上过程直到所有点都在访问集合中

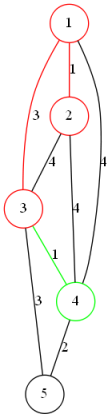
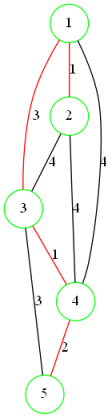
Kruskal算法：（并查集思想）

　　将边按照权值排序
　　依次枚举每一条边，若连接的两点不连通则加入最小生成树中
　　使用并查集维护连通性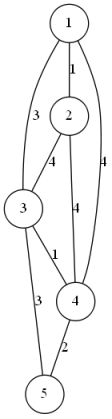

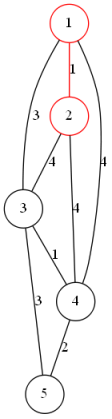
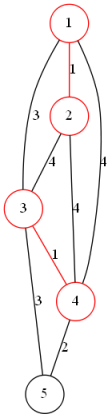
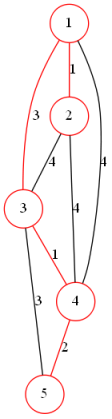
模板代码：

 1 int f[101], h;
 2 struct node{
 3     int x, y, l;
 4 } a[100001];
 5 inline bool cmp(node i, node j){
 6     return i.l < j.l;
 7 }
 8 inline int find(int x){
 9     if(x != f[x])//本身是否为父亲节点
10         f[x] = find(f[x]);
11     return f[x];
12 }//并查集操作
13 int main(){
14     for(int i = 1; i <= n; i++){
15         f[i] = i;
16     }//父节点初始化
17     sort(a+1, a+k+1, cmp);//排序
18     for(int i = 1; i <= k; i++){
19         int r1 = find(a[i].x);
20         int r2 = find(a[i].y);
21         if(r1 != r2){
22             f[r1] = r2;
23         }
24     }
25 }

Kruskal

#include<bits/stdc++.h>
using namespace std;
int n,m,a,b,c;
int sum;
int g[1001][1001],minn[1001];
bool u[1001]; 
int main(){
    memset(g,0x7f,sizeof(g));
    memset(minn,0x7f,sizeof(minn));
    memset(u,true,sizeof(u));
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>a>>b>>c;
        g[a][b]=g[b][a]=c;
        sum+=c;
    }
    minn[1]=0;
    for(int i=1;i<=n;i++){
        int k=0;
        for(int j=1;j<=n;j++)
        if(u[j]&&minn[j]<minn[k])
        k=j;  
        u[k]=false;
        for(int j=1;j<=n;j++)
        if(u[j]&&g[k][j]<minn[j])
        minn[j]=g[k][j];
    }
    int total=0;
    for(int i=1;i<=n;i++) 
    total+=minn[i];
    cout<<sum-total<<endl;
    return 0;
}

Prim

模板题：

洛谷P3366【模板】最小生成树：

题目链接：https://www.luogu.org/problemnew/show/P3366

思路：（Kruskal）

一道模板题，首先用一个结构体读入，然后初始化父节点，再按边权排序，然后用find函数分别找输入时的两个点的父节点，并判断其中一个是否是另一个的父亲，否则就进行合并，并将h+=a[i].l。（思路比较好理解）

 1 #include<cstdio>
 2 #include<iostream>
 3 #include<algorithm>
 4 
 5 using namespace std;
 6 
 7 int h, f[200005];
 8 
 9 struct node{
10     int x, y, l;
11 } a[200005];
12 
13 inline bool cmp(node i, node j){
14     return i.l < j.l;
15 }
16 
17 inline int find(int x){
18     if(x != f[x])
19         f[x] = find(f[x]);
20     return f[x];
21 }
22 
23 int main(){
24     int n, m;
25     scanf("%d%d", &n, &m);
26     for(int i = 1; i <= n; i++){
27         f[i] = i;
28     }
29     for(int i = 1; i <= m; i++){
30         scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].l);
31         //h += a[i].l;
32     }
33     sort(a+1, a+m+1, cmp);
34     for(int i = 1; i <= m; i++){
35         int r1 = find(a[i].x);
36         int r2 = find(a[i].y);
37         if(r1 != r2){
38             f[r1] = r2;
39             h += a[i].l;
40             //h -= a[i].l;
41         }
42     }
43     printf("%d", h);
44     return 0;
45 }

AC代码

洛谷P2820 局域网：

题目链接：https://www.luogu.org/problemnew/show/P2820

思路：

首先这道题的问法就很模板：

很显然“f(i,j)表示i,j之间连接的畅通程度”即为i到j点的权值；“除去一些连线，使得网络中没有回路，并且被除去网线的Σf(i,j)最大”很显然是求最小生成树。但注意一个细节，它与最小生成树有所不同，它要求的是Σf(i,j)最大。

所以我们在最小生成树的模板上进行修改即可：读入时将所有的边权都加到h中。在判断父节点是否相同时，若不同，则将合并，并将合并的这条边的权值减掉即可。

 1 #include<cstdio>
 2 #include<iostream>
 3 #include<algorithm>
 4 
 5 using namespace std;
 6 
 7 int f[101], h;
 8 
 9 struct node{
10     int x, y, l;
11 } a[100001];
12 
13 inline bool cmp(node i, node j){
14     return i.l < j.l;
15 }
16 
17 inline int find(int x){
18     if(x != f[x])
19         f[x] = find(f[x]);
20     return f[x];
21 }
22 
23 int main(){
24     int n, k;
25     scanf("%d%d", &n, &k);
26     for(int i = 1; i <= n; i++){
27         f[i] = i;
28     }
29     for(int i = 1; i <= k; i++){
30         scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].l);
31         h += a[i].l;
32     }
33     sort(a+1, a+k+1, cmp);
34     for(int i = 1; i <= k; i++){
35         int r1 = find(a[i].x);
36         int r2 = find(a[i].y);
37         if(r1 != r2){
38             f[r1] = r2;
39             h -= a[i].l;
40         }
41     }
42     printf("%d", h);
43     return 0;
44 }