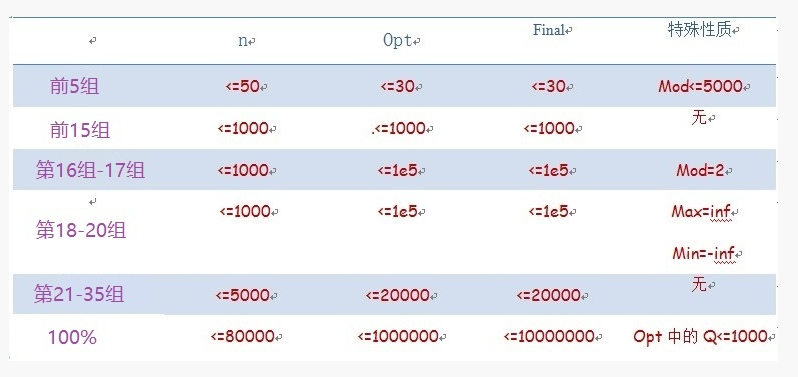
题面

分析
看着数据规模很大,实际上Q只有1000组,后面都是无修改的询问了。
于是考虑到差分区间修改,可以达到O(1)的效率,而每次查询的时候再O(N)计算差分数组的前缀和即可。
对于后面不带修改的询问,只需要O(N)维护前缀和
时间复杂度O(N*Q)。其实感觉就是个暴力qvq
代码
- #include<bits/stdc++.h>
- using namespace std;
- #define N 800080
- #define ll long long
- ll minx,maxx,mod,n,q,l,r,x,ans,now,final;
- char op[10];
- ll a[N],c[N],sum[N];
- template<class T>
- inline void read(T &x)
- {
- x=0;ll f=1;static char c=getchar();
- while(c<'0'||c>'9') {if(c=='-')f=-1;c=getchar();}
- while(c>='0'&&c<='9'){x=x*10+c-'0',c=getchar();}
- x*=f;
- }
- int main()
- {
- read(n);read(q);read(mod);read(minx);read(maxx);
- while(q--)
- {
- scanf("%s",op);
- if(op[0]=='A')
- {
- read(l),read(r),read(x);
- c[l]+=x;c[r+1]-=x;
- }
- else
- {
- ans=0;now=0;
- read(l);read(r);
- for(ll i=1;i<=r;i++)
- {
- now+=c[i];
- if(i>=l&&(now*i)%mod>=minx&&(now*i)%mod<=maxx)
- ans++;
- }
- printf("%lld ",ans);
- }
- }
- read(final);
- for(ll i=1;i<=n;i++)
- {
- a[i]=a[i-1]+c[i];
- if((a[i]*i)%mod>=minx&&(a[i]*i)%mod<=maxx)sum[i]=sum[i-1]+1;
- else sum[i]=sum[i-1];
- }
- while(final--)
- {
- read(l);read(r);
- printf("%lld ",sum[r]-sum[l-1]);
- }
- return 0;
- }