题目链接
题解
看题型显然插头(dp)
考虑如何设计状态
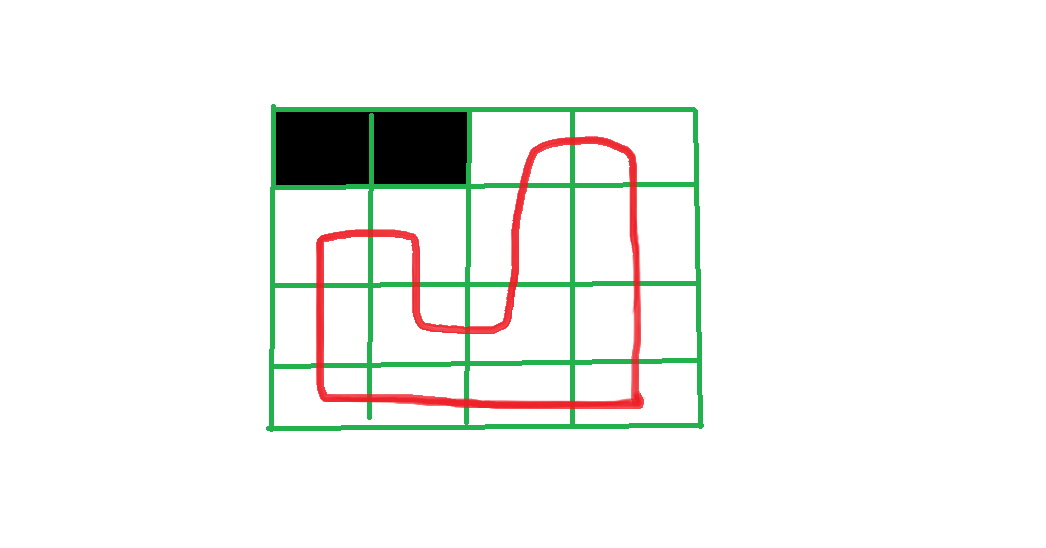
有这样一个方案
当我们决策到某个位置
轮廓线长这样
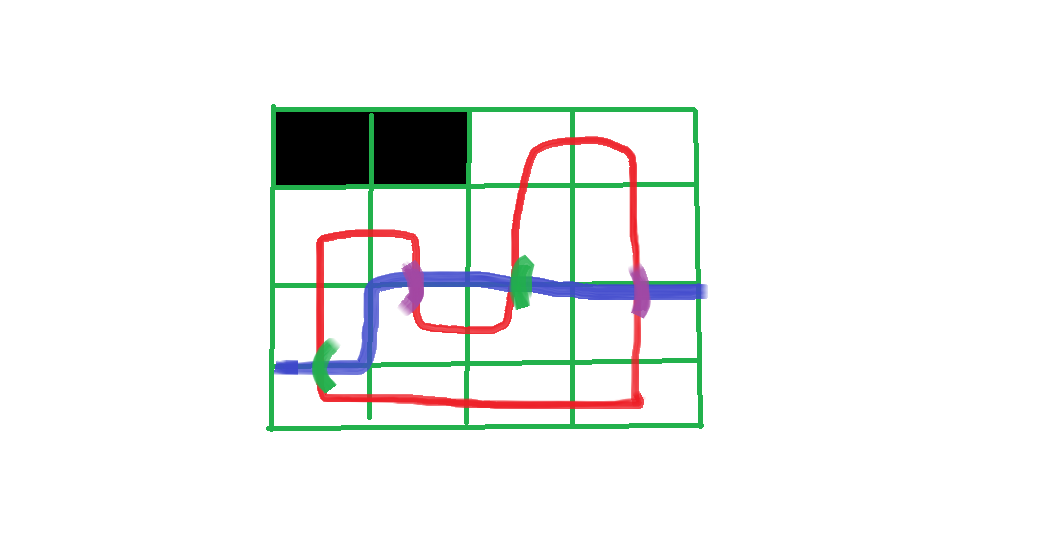
你会发现插头一定是相互匹配的
所以我们实际上可以把状态用括号序列表示
如上图就是(#)()
是一个三进制数
那么我们设(f[i][j][s])表示决策到((i,j)),轮廓线状态为(s)的方案数
我们同时记(0)为空插头,(1)为表示左括号的插头,(2)为表示有括号的插头
先不管空间问题,我们考虑一下转移
有比较多的情况
我们记(b1),(b2)为((i,j))的左、上插头
(b1 = 0,b2 = 0)
首先如果((i,j))本身是障碍格,那么它右插头和下插头也为(0)
否则如果对应方向没有障碍,((i,j))右下插头为(12)
(b1)和(b2)有一者为(0),那么转移的时候另一个括号的位置放哪里都可以,只需要判断有无障碍
(b1)和(b2)为同一种括号,我们只需往另一侧查找匹配的括号,改变方向
例如((#))变为###()
如图所示:
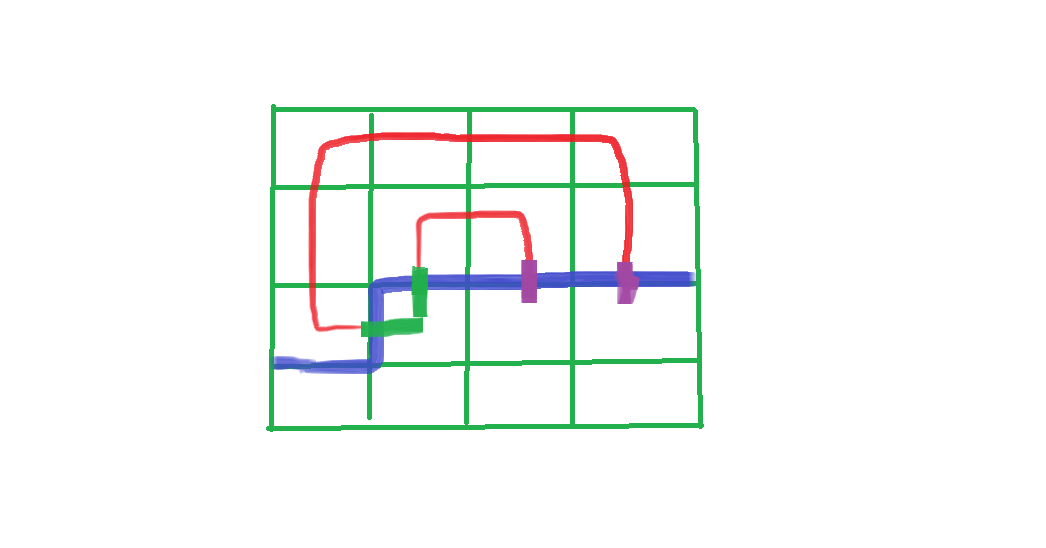
把左边两个连起来,右边两个插头就变成了匹配的括号
即由((#))变为###()
(b1 = 2)且(b2 = 1)
就是(#)(#)这种情况,可以变为(####)
(b1 = 1)且(b2 = 2)
除非是最后一个格子,否则不能贸然连起来,不然就会出现不连通的情况
具体实现的时候,可以使用四进制而结合位运算加快速度
由于空间比较小,我们需要滚动数组,并且使用(hash)表储存状态
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<map>
#include<vector>
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define mp(a,b) make_pair<int,int>(a,b)
#define cls(s) memset(s,0,sizeof(s))
#define cp pair<int,int>
#define LL long long int
using namespace std;
const int maxn = 13,maxm = 5000000,INF = 1000000000,P = 201611;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
return out * flag;
}
int n,m,sx,sy;
char S[maxn][maxn];
int now,tot[2],h[2][P],nxt[2][maxm],num[2][maxm];
LL f[2][maxm],ans;
inline void add(int s,LL x){
int tmp = s % P;
for (int k = h[now][tmp]; k; k = nxt[now][k])
if (num[now][k] == s){f[now][k] += x; return;}
nxt[now][++tot[now]] = h[now][tmp]; h[now][tmp] = tot[now];
num[now][tot[now]] = s; f[now][tot[now]] = x;
}
inline bool isok(int x,int y){
return x >= 1 && x <= n && y >= 1 && y <= m && S[x][y] != '*';
}
void work(){
int las = 1,e,s,b1,b2;
LL x;
f[0][1] = tot[0] = 1; num[0][1] = 0;
for (int i = 1; i <= n; i++){
for (int k = 1; k <= tot[now]; k++) num[now][k] <<= 2;
for (int j = 1; j <= m; j++){
now ^= 1; las ^= 1;
cls(h[now]); tot[now] = 0;
for (int k = 1; k <= tot[las]; k++){
s = num[las][k]; x = f[las][k];
b1 = (s >> (j - 1 << 1)) & 3;
b2 = (s >> (j << 1)) & 3;
e = s ^ (b1 << (j - 1 << 1)) ^ (b2 << (j << 1));
if (b1 == 0 && b2 == 0){
if (S[i][j] == '*') add(e,x);
else if (isok(i + 1,j) && isok(i,j + 1))
add(e | (1 << (j - 1 << 1)) | (2 << (j << 1)),x);
}
else if (b1 == 0){
if (isok(i,j + 1)) add(s,x);
if (isok(i + 1,j)) add(e | (b2 << (j - 1 << 1)),x);
}
else if (b2 == 0){
if (isok(i + 1,j)) add(s,x);
if (isok(i,j + 1)) add(e | (b1 << (j << 1)),x);
}
else if (b1 == 1 && b2 == 1){
int cnt = 1;
for (int p = j + 1; p <= m + 1; p++){
if ((e >> (p << 1) & 3) == 1) cnt++;
if ((e >> (p << 1) & 3) == 2) cnt--;
if (!cnt){add(e ^ (3 << (p << 1)),x); break;}
}
}
else if (b1 == 2 && b2 == 2){
int cnt = 1;
for (int p = j - 2; ~p; p--){
if ((e >> (p << 1) & 3) == 2) cnt++;
if ((e >> (p << 1) & 3) == 1) cnt--;
if (!cnt){add(e ^ (3 << (p << 1)),x); break;}
}
}
else if (b1 == 2 && b2 == 1) add(e,x);
else if (i == sx && j == sy) ans += x;
}
}
}
printf("%lld
",ans);
}
int main(){
n = read(); m = read();
REP(i,n) scanf("%s",S[i] + 1);
REP(i,n) REP(j,m) if (S[i][j] == '.') sx = i,sy = j;
work();
return 0;
}