手写字体识别模型LeNet5诞生于1994年,是最早的卷积神经网络之一。原文地址为Gradient-Based Learning Applied to Document Recognition,感谢网络中各博主的讲解,尤其是该博客,帮助我的理解,感谢。
- Model详解
- Model概览
- 代码复现
下图就是我们很熟悉的LeNet-5的结构图,LeNet5由7层CNN(不包含输入层)组成,输入的原始图像大小是32×32像素,卷积层用Ci表示,池化层用Si表示,全连接层用Fi表示。接下来就将对其进行逐层介绍:
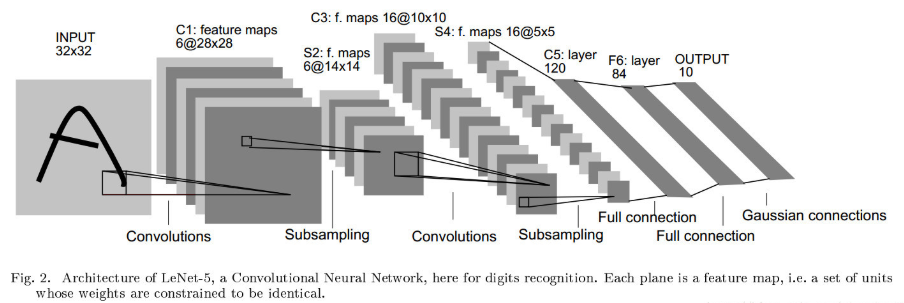
C1层有6个28x28的特征图组成,每个特征图中的任一个元素与该层的输入中一个5x5的区域相连接。每个Filter中包含了25个参数和转置参数Bias都是可训练的数据,故C1层中共有(5*5+1)*6 = 156个可训练的参数。C1层一共产生了(32-5+1)*(32-5+1) = 28*28 个神经元。
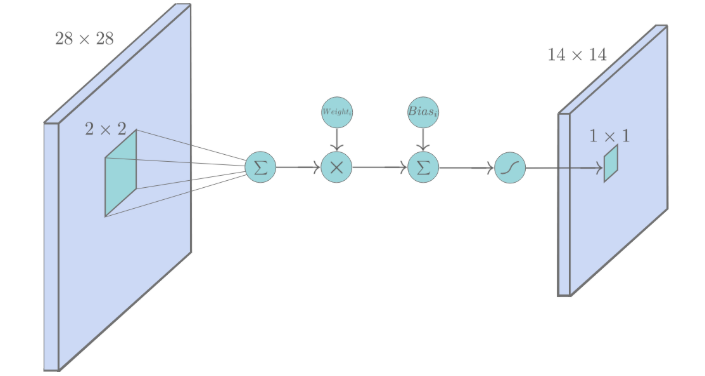
S2层是一个池化层,由6个14x14的特征图组成,每一个特征图中元素都与C1层中对应的特征图中一个2x2的相邻区域相连。与常见的池化不同,该模型中,池化单元之间没有重叠,在池化区域内进行聚合统计后得到新的特征值,相当于图像大小减半,因此卷积后的28×28图像经2×2池化后就变为14×14,而图像的个数没有改变。
在这一层计算的过程中:2×2 单元里的值相加,然后再乘以训练参数w,再加上一个偏置参数b,然后取sigmoid值(S函数:0-1区间),作为对应的该单元的值。
S2层中一共有(1+1×6 = 12个可训练的参数(每一个特征图共享相同的w和b)。
C3层由16个10x10的特征图组成,卷积模板大小为5×5。
与C1的最大区别是,这里每个特征图中的元素会与S2层中若干个特征图中处于相同位置的5x5的区域相连,C3与S2并不是全连接而是部分连接,有些是C3连接到S2三层、有些四层、甚至达到6层,具体由下图展示
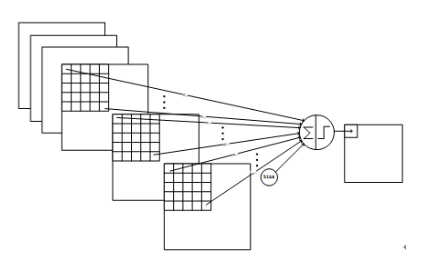

例如第一列表示C3层的第0个特征图只跟S2层的第0、1和2这三个feature maps相连接,计算过程为:用3个卷积模板分别与S2层的3个feature maps进行卷积,然后将卷积的结果相加求和,再加上一个偏置,再取sigmoid得出卷积后对应的feature map了。
因此,C3层的参数数目为(5×5×3+1)×6 +(5×5×4+1)×9 +5×5×6+1 = 1516。
(问题1)为什么要采用这样的连接方案?
- 可以有效地减少参数和连接数
- 不对称的连接,可以使本层的特征图对应不同的高级特征。
与S2层类似,池化单位为2×2,因此,该层与C3一样共有16个特征图,每个特征图的大小为5×5。 共有32个可求参数。
C5是一个类似C3的卷积层,核大小为5×5,该层由120个1x1的特征图组成。
与C3层不同的是,这里的连接是一种全连接(巧妙地设计), 本层的可训练参数有 120×(5×5×16+1) = 48120 个
F6就是一个简单的全连接层,它由84个神经元构成。和传统的全连接一样每个神经元将C5层中的特征图的值乘上相应的权重并相加,再加上对应的偏置再经过激活函数(tanh / sigmoid)。
该层有84个特征图,F6层共有84×(120+1)=10164个可训练的参数。
输出层由10个欧几里得径向基函数核(Euclidean Radial Basis Function, RBF)构成,每个核对应0-9中的一个类别。输出值最小的那个核对应的i就是这个模型识别出来的数字。
RBF:
上式中的Wij的值由i的比特图编码确定,i从0到9,j取值从0到7×12-1。RBF输出的值越接近于0,表示当前网络输入的识别结果与字符i越接近。
该层共有84 × (120+1) = 10164个可训练参数

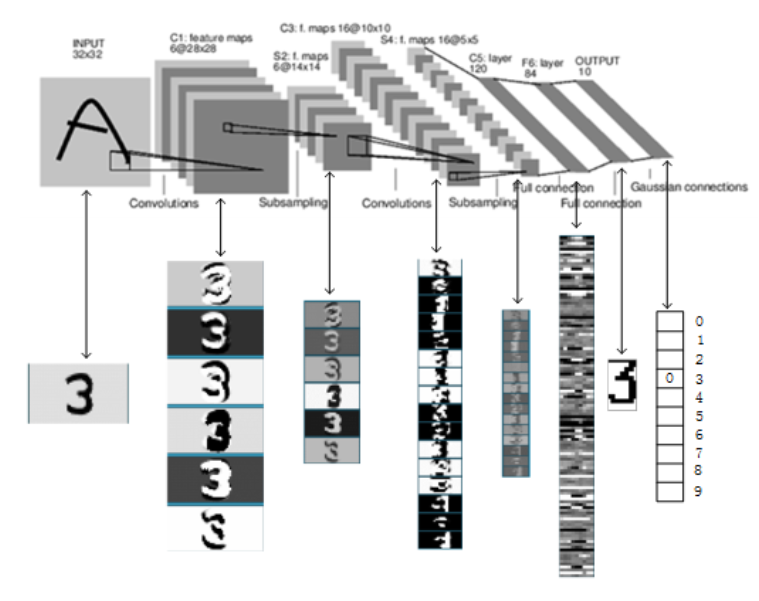
【复现】
tensorflow:1.13.1 + python 3.6
简化的LeNet,paddling都为‘Same’模式,故特征图的大小有所差异。
# In[ ]:
import tensorflow.examples.tutorials.mnist.input_data as input_data
import tensorflow as tf
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
# In[ ]:
x = tf.placeholder('float', shape=[None, 28*28])
y_true = tf.placeholder('float', shape=[None, 10])
x_image = tf.reshape(x, [-1, 28, 28, 1])
def weights(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(x, W):
return tf.nn.conv2d(input=x, filter=W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# In[ ]:
# 1st layer: conv+relu+max_pool
w_conv1 = weights([5, 5, 1, 6])
b_conv1 = bias([6])
h_conv1 = tf.nn.relu(conv2d(x_image, w_conv1)+b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
# 2nd layer: conv+relu+max_pool
w_conv2 = weights([5, 5, 6, 16])
b_conv2 = bias([16])
h_conv2 = tf.nn.relu(conv2d(h_pool1, w_conv2)+b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*16])
# 3rd layer: 3*full connection
w_fc1 = weights([7*7*16, 120])
b_fc1 = bias([120])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, w_fc1)+b_fc1)
w_fc2 = weights([120, 84])
b_fc2 = bias([84])
h_fc2 = tf.nn.relu(tf.matmul(h_fc1, w_fc2)+b_fc2)
w_fc3 = weights([84, 10])
b_fc3 = bias([10])
h_fc3 = tf.nn.softmax(tf.matmul(h_fc2, w_fc3)+b_fc3)
# In[ ]:
cross_entropy = -tf.reduce_sum(y_true*tf.log(h_fc3))
train_step = tf.train.AdamOptimizer(1e-3).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(h_fc3, 1), tf.argmax(y_true, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, 'float'))
# In[ ]:
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
for i in range(1000):
batch = mnist.train.next_batch(60)
if i%100 == 0:
train_accuracy = accuracy.eval(session=sess, feed_dict={x: batch[0], y_true: batch[1]})
print('step {}, training accuracy: {}'.format(i, train_accuracy))
train_step.run(session=sess, feed_dict={x: batch[0], y_true: batch[1]})
print('test accuracy: {}'.format(accuracy.eval(session=sess, feed_dict={x: mnist.test.images, y_true:
mnist.test.labels})))

