•何为主席树
图1
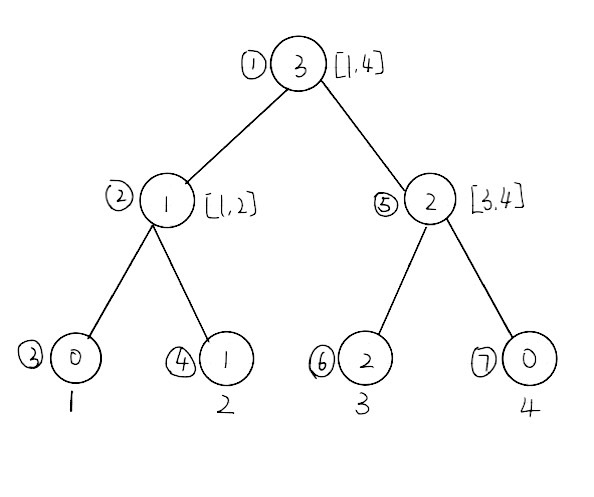
主席树的构造如图，以前序遍历的方式编号，叶子表示1到n
因为叶子是1到n，就有了左子树总是小于右子树的性质
除叶子外的节点记录的是区间sum代表这个节点的叶子有多少个数
如图 区间[2,2]有1个数，区间[3,3]有1个数
所以区间[1,2]有1个数，区间[3,4]有2个数，区间[1,4]有3个数
•性质
- 左子树总是小于右子树
因为从左到右叶子是1到n
设树的sum=x+y，左子树sum=x，右子树sum=y
所以在找第k小的时候,由于左子树小于右子树，所以前x小肯定在左子树上，第x+1到第x+y小在右子树上
当k<=x时，就在左子树上找，当k>x时在右子树上找，
在右子树上找时，由于右子树第一个是第x+1小，所以找第k小也就是找右子树的第k-x小
- 区间可减性
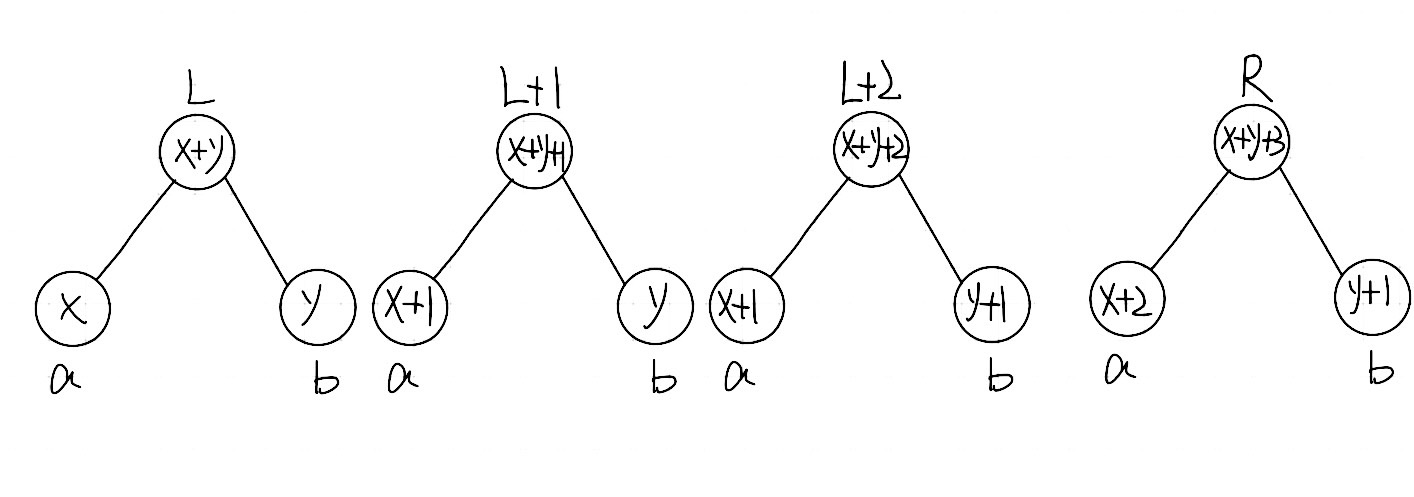
由于sum记录的是个数，假设现在是第L棵树，经过n次操作变成第R棵树
由于每次操作都是修改一次，所以R的左子树sum-L的左子树sum=从L到R的左子树的操作数
所以求[L,R]区间的第k小，可以利用R的左子树sum-L的左子树sum即为[L,R]内左子树上的数的个数
图2
如图 经过(L,R]区间的增加的左子树的个数为2，也就是R的左子树sum-L的左子树的sum
•例题
这个题是可持久化的题，并非完全的主席树
这个题的叶子的值不是1到n，而是根据输入而定
也没有用到上述的性质
利用这个题来学习可持久化，为主席树做铺垫
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1e6+5; 4 struct Node 5 { 6 int l,r; 7 int num;///num为值，这里与主席树不同 8 Node(){num=0;} 9 }seg[maxn*20]; 10 int root[maxn],a[maxn]; 11 int cnt=0; 12 void build(int l,int r,int &rt)///以前序遍历的方式建树 13 { 14 rt=++cnt;///rt为编号 15 if(l==r) 16 { 17 seg[rt].num=a[l]; 18 return ; 19 } 20 int mid=(r+l)>>1; 21 build(l,mid,seg[rt].l); 22 build(mid+1,r,seg[rt].r); 23 } 24 25 void update(int l,int r,int &rt,int pos,int y) 26 { 27 seg[++cnt]=seg[rt];///复制前一棵树 28 rt=cnt;///处理所新建的这棵树 29 if(l==r) 30 { 31 seg[rt].num=y; 32 return ; 33 } 34 int mid=(r+l)>>1; 35 if(pos<=mid) update(l,mid,seg[rt].l,pos,y); 36 else update(mid+1,r,seg[rt].r,pos,y); 37 } 38 39 int query(int l,int r,int rt,int pos) 40 { 41 if(l==r) return seg[rt].num; 42 int mid=(r+l)>>1; 43 if(pos<=mid) return query(l,mid,seg[rt].l,pos); 44 else return query(mid+1,r,seg[rt].r,pos); 45 } 46 47 int main() 48 { 49 ios::sync_with_stdio(0); 50 int n,m; 51 cin>>n>>m; 52 for(int i=1;i<=n;i++) 53 cin>>a[i]; 54 build(1,n,root[0]); 55 int pre,op,x,y; 56 for(int i=1;i<=m;i++) 57 { 58 cin>>pre>>op>>x; 59 if(op==1) 60 { 61 cin>>y; 62 root[i]=root[pre]; 63 update(1,n,root[i],x,y); 64 } 65 else 66 { 67 cout<<query(1,n,root[pre],x)<<endl; 68 root[i]=root[pre]; 69 } 70 } 71 }主席树的模板题，用到了上述的性质
由于刚开始没有值，我就没有建树
其实做模板的话可以建一个空树
由于叶子是从1到n的，所以对于给出的数一般要离散化一下，使得对应1到n
View Code1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 #define ll long long 5 const int maxn=1e5+5; 6 int cnt,root[maxn];///每棵树的根 7 int index[maxn];///按值大小排序后的序号 8 struct node 9 { 10 int l,r; 11 int sum; 12 node(){sum=0;} 13 }seg[maxn*40]; 14 struct value 15 { 16 int v; 17 int id; 18 }V[maxn]; 19 bool cmp(value a,value b) 20 { 21 return a.v<b.v; 22 } 23 24 void init() 25 { 26 cnt=0; 27 seg[0].l=0,seg[0].r=0; 28 root[0]=0; 29 } 30 31 void build(int l,int r,int &rt)///以前序遍历的方式建树 32 { 33 rt=++cnt;///rt为编号 34 if(l==r) 35 return ; 36 int mid=(r+l)>>1; 37 build(l,mid,seg[rt].l); 38 build(mid+1,r,seg[rt].r); 39 } 40 41 void update(int l,int r,int &rt,int pos) 42 { 43 seg[++cnt]=seg[rt];///复制前一棵树 44 rt=cnt;///因为对新树进行操作，是rt为新树 45 seg[rt].sum++;///进行操作了，个数+1 46 47 if(l==r) return ; 48 int mid=(l+r)>>1; 49 if(mid>=pos) 50 update(l,mid,seg[rt].l,pos); 51 else 52 update(mid+1,r,seg[rt].r,pos); 53 } 54 55 int query(int L,int R,int l,int r,int k) 56 { 57 int d=seg[seg[R].l].sum-seg[seg[L].l].sum;///利用区间可减性，左子树上一共有d个数 58 if(l==r) return l; 59 int mid=(l+r)>>1; 60 if(d>=k)///利用 左子树<右子树 前d个在左子树上，其他的在右子树上 61 return query(seg[L].l,seg[R].l,l,mid,k); 62 else///右子树第一个是第d+1个 找第k个也就是找右子树的第k-d个 63 return query(seg[L].r,seg[R].r,mid+1,r,k-d); 64 65 } 66 67 int main() 68 { 69 int n,m; 70 cin>>n>>m; 71 for(int i=1;i<=n;i++) 72 { 73 cin>>V[i].v; 74 V[i].id=i; 75 } 76 ///离散化 77 sort(V+1,V+1+n,cmp); 78 for(int i=1;i<=n;i++) 79 index[V[i].id]=i; 80 init(); 81 // build(1,n,root[0]); 82 for(int i=1;i<=n;i++) 83 { 84 root[i]=root[i-1];///复制前一个树 85 update(1,n,root[i],index[i]); 86 } 87 int L,R,k; 88 for(int i=1;i<=m;i++) 89 { 90 cin>>L>>R>>k; 91 cout<<V[query(root[L-1],root[R],1,n,k)].v<<endl; 92 } 93 }查询$[L,R]$区间里有多少个数不大于k
只需要修改一下query函数
把k也离散化一下，利用k是第x小，答案就是
第R棵树的[0,k]数量-第(L-1)棵树的[0,k]数量
因为这个题是从$L,Repsilon[0,n-1]$而不是从$1$开始，需要注意坑点
因为是从$1$到$n$的树，需要记得$L++,R++$
因为离散化后会从$kepsilon[0,n]$,所有需要从0开始建树更新查询，防止从$1$开始找不到$0$位置
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1e5+5; 4 struct node 5 { 6 int l,r; 7 int sum; 8 node(){sum=0;} 9 }seg[maxn*20]; 10 int root[maxn]; 11 int cnt=0; 12 int a[maxn],b[maxn]; 13 14 void Init() 15 { 16 cnt=0; 17 root[0]=0; 18 seg[0].l=0,seg[0].r=0; 19 } 20 21 void build(int l,int r,int &rt) 22 { 23 rt=++cnt; 24 if(l==r) return ; 25 int mid=(l+r)>>1; 26 build(l,mid,seg[rt].l); 27 build(mid+1,r,seg[rt].r); 28 } 29 30 void update(int l,int r,int &rt,int pos) 31 { 32 seg[++cnt]=seg[rt]; 33 rt=cnt; 34 seg[rt].sum++; 35 if(l==r) 36 return ; 37 int mid=(r+l)>>1; 38 if(pos<=mid) return update(l,mid,seg[rt].l,pos); 39 else return update(mid+1,r,seg[rt].r,pos); 40 } 41 42 43 ///query第R棵树的[0,k]数量-第(L-1)棵树的[0,k]数量 44 ///询问方法1 45 int query1(int L,int R,int l,int r,int k) 46 { 47 if(l==r)///[0,k]中某个位置的增量 48 return seg[R].sum-seg[L].sum; 49 int mid=(l+r)>>1; 50 if(mid>=k) 51 return query(seg[L].l,seg[R].l,l,mid,k); 52 else///递归右子树，需要加上左子树的增量 53 { 54 int d=seg[seg[R].l].sum-seg[seg[L].l].sum; 55 return d+query(seg[L].r,seg[R].r,mid+1,r,k); 56 } 57 } 58 ///询问方法2 59 int query2(int rt,int l,int r,int k) 60 { 61 if(l==r) 62 return seg[rt].sum; 63 int mid=(r+l)>>1; 64 if(mid>=k) 65 return query(seg[rt].l,l,mid,k); 66 else 67 return seg[seg[rt].l].sum+query(seg[rt].r,mid+1,r,k); 68 } 69 70 71 int main() 72 { 73 // freopen("C:\Users\14685\Desktop\C++workspace\in&out\contest","r",stdin); 74 int t; 75 cin>>t; 76 for(int T=1;T<=t;T++) 77 { 78 int n,m; 79 cin>>n>>m; 80 for(int i=1;i<=n;i++) 81 cin>>a[i],b[i]=a[i]; 82 83 sort(b+1,b+1+n); 84 int len=unique(b+1,b+n+1)-(b+1); 85 Init(); 86 build(0,len,root[0]); 87 for(int i=1;i<=n;i++) 88 { 89 root[i]=root[i-1]; 90 update(0,len,root[i],upper_bound(b+1,b+1+len,a[i])-b-1); 91 } 92 93 printf("Case %d: ",T); 94 95 while(m--) 96 { 97 int L,R,k; 98 cin>>L>>R>>k; 99 L++,R++; 100 k=upper_bound(b+1,b+1+len,k)-b-1; 101 // cout<<query1(root[L-1],root[R],1,len,k)<<endl; 102 cout<<query2(root[R],0,len,k)-query2(root[L-1],0,len,k)<<endl; 103 } 104 } 105 }
