
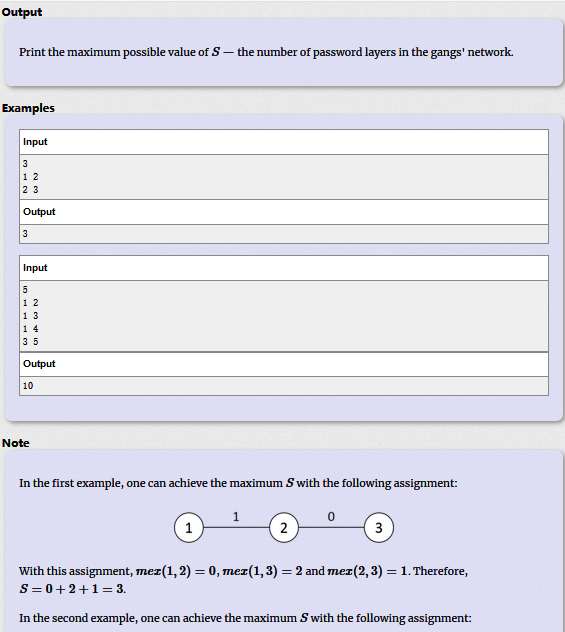
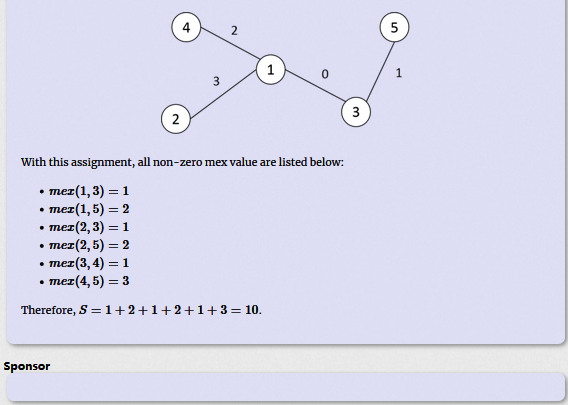
题意: 给你一棵树,将0~n-2一一赋值给n-1条边,则S最大可能取值
S=∑1≤u<v≤nmex(u,v)=∑1≤x≤n(∑mex(u,v)=xx)=∑1≤x≤n(∑mex(u,v)≥x1)
所以我们只需要考虑每条边的贡献即可,每条边要有贡献。
首先我们可以看0所在的边的两个端点u,v,则0的贡献为size[v][u]*size[u][v],接着看1,我们发现只有将0,1连接在一起贡献才会尽可能的大,所以我们要使得[0,m]分布在一条链上。所以我们可以对这棵树进行dp,dp[u][v]表示以u,v为端点的链

1 #include<bits/stdc++.h> 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<string> 6 #include<algorithm> 7 #include<stack> 8 #include<queue> 9 using namespace std; 10 typedef long long ll; 11 const int mod=1e9+7; 12 const int N=3e3+5; 13 14 vector<int>G[N]; 15 int fa[N][N],sz[N][N]; 16 ll dp[N][N],ans; 17 18 void dfs(int u,int f,int root){ 19 sz[root][u]=1; 20 fa[root][u]=f; 21 for(auto v: G[u]){ 22 if(v==f) 23 continue; 24 dfs(v,u,root); 25 sz[root][u]+=sz[root][v]; 26 } 27 } 28 29 ll sl(int x,int y){ 30 if(x==y) 31 return 0; 32 if(dp[x][y]!=-1) 33 return dp[x][y]; 34 dp[x][y]=1ll*sz[y][x]*sz[x][y]+max(sl(fa[y][x],y),sl(x,fa[x][y])); 35 return dp[x][y]; 36 } 37 38 int main(){ 39 #ifdef Mizp 40 freopen("in.txt","r",stdin); 41 #endif 42 std::ios::sync_with_stdio(0); 43 int n; 44 cin>>n; 45 for(int i=1;i<n;i++){ 46 int u,v; 47 cin>>u>>v; 48 G[u].push_back(v); 49 G[v].push_back(u); 50 } 51 52 for(int i=1;i<=n;i++){ 53 dfs(i,0,i); 54 } 55 memset(dp,-1,sizeof dp); 56 for(int i=1;i<=n;i++){ 57 for(int j=1;j<=n;j++){ 58 ans=max(ans,sl(i,j)); 59 } 60 } 61 cout<<ans<<endl; 62 return 0; 63 }
1 #include<bits/stdc++.h> 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<string> 6 #include<algorithm> 7 #include<stack> 8 #include<queue> 9 using namespace std; 10 typedef long long ll; 11 const int mod=1e9+7; 12 const int N=3e3+5; 13 14 vector<int>G[N]; 15 int fa[N][N],sz[N][N]; 16 ll dp[N][N],ans; 17 18 void dfs(int u,int f,int root){ 19 sz[root][u]=1; 20 fa[root][u]=f; 21 for(auto v: G[u]){ 22 if(v==f) 23 continue; 24 dfs(v,u,root); 25 sz[root][u]+=sz[root][v]; 26 } 27 } 28 29 ll sl(int x,int y){ 30 if(x==y) 31 return 0; 32 if(dp[x][y]!=-1) 33 return dp[x][y]; 34 dp[x][y]=1ll*sz[y][x]*sz[x][y]+max(sl(fa[y][x],y),sl(x,fa[x][y])); 35 return dp[x][y]; 36 } 37 38 int main(){ 39 #ifdef Mizp 40 freopen("in.txt","r",stdin); 41 #endif 42 std::ios::sync_with_stdio(0); 43 int n; 44 cin>>n; 45 for(int i=1;i<n;i++){ 46 int u,v; 47 cin>>u>>v; 48 G[u].push_back(v); 49 G[v].push_back(u); 50 } 51 52 for(int i=1;i<=n;i++){ 53 dfs(i,0,i); 54 } 55 memset(dp,-1,sizeof dp); 56 for(int i=1;i<=n;i++){ 57 for(int j=1;j<=n;j++){ 58 ans=max(ans,sl(i,j)); 59 } 60 } 61 cout<<ans<<endl; 62 return
