逻辑回归（1）

代码思路：

1、读取数据	read_scv
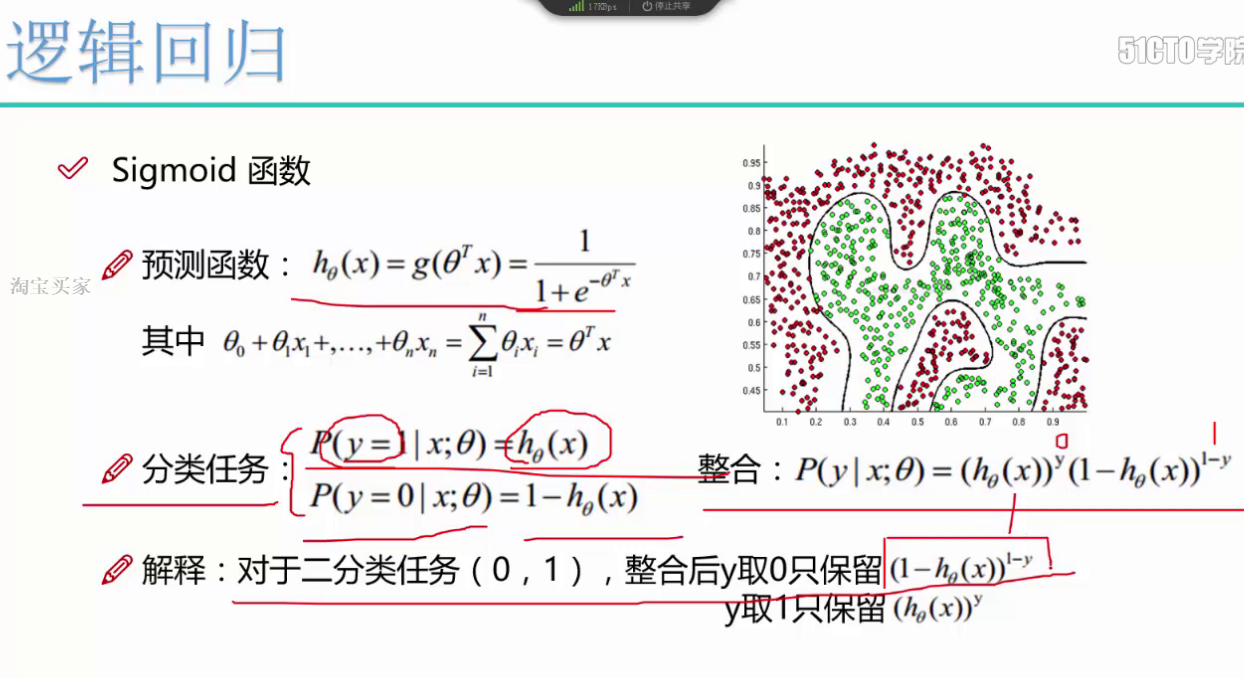
2、预测模型函数：①sigmoid函数②预测函数	#sigmoid函数 def sigmoid(z): return 1/(1+np.exp(-z)) #计算预测模型的函数 def model(X,theta): return sigmoid(np.dot(X,theta.T))
3、目标函数（似然函数）	#计算目标值的函数（对数似然） def cost(X,Y,theta): h=model(X,theta) left=np.multiply(-Y,np.log(h)) right=np.multiply(1-Y,np.log(1-h)) return np.sum(left-right)/(len(X))
4、计算梯度的函数：	#计算梯度的函数 def gradient(X,Y,theta): grad=np.zeros(theta.shape) error=(model(X,theta0)-Y).ravel() for j in range(len(theta.ravel())): term=np.multiply(error,X[:,j]) grad[j]=np.sum(term) / len(X) return grad
5、梯度下降的函数（更新梯度值）：	#对X，Y数据重新打乱（小批量梯度下降有用） import numpy.random def shuffleData(data):     np.random.shufflr(data)     cols=data.shape[1]     X=data[:,0:cols-1]     Y=data[:,cols-1:]     return X,Y #比较三种不同梯度下降方法 STOP_ITER=0 STOP_COST=1 STOP_GRAD=2 def stopCriterion(type,value,threshold): #设定三种不同的停止策略 if type==STOP_ITER: return value>threshold elif type==STOP_COST: return abs(value[-1]-value[-2]<threshold) elif type==STOP_GRAD: return np.linalg.norm(value)<threshold import time def descent(X,Y,theta,batchSize,stopType,thresh,alpha): init_time=time.time() i=0 #迭代次数 k=0 #batch grad=np.zeros(theta,shape) #计算的梯度 costs=[cost(X,Y,theta)] #计算损失值 while True: grad=gradient(X[k:k+batchSize],Y[k:k+batchSize],theta) k+=batchSize #取batch数量个数据 if k>=n: k=0 X,Y=shuffleData(data)#重新洗牌 theta=theta-alpha*grad#参数更新 costs.append(cost(X,Y,theta))#计算新的损失 i+=1 if stopType==STOP_ITER: value=i elif stopType==STOP_COST: value=costs elif stopType==STOP_GRAD: value=grad if stopCriterion(stopType,value,thresh): break return theta,i-1,costs,grad,time.time()-init.time
6、测试	#训练数据 theta0=np.array([0.0,0.0,0.0]) X_train.insert(0,'ones',1) X=X_train.as_matrix() Y=Y_train.as_matrix() print(cost(X,Y,theta0)) print(gradient(X,Y,theta0))

1、sigmoid函数：（也是预测函数）

2、逻辑回归过程：（目标函数）

（将目标函数转化成对数似然函数）

3、求导过程：