高数学习笔记之范数与距离度量(python实现)

0x00 范数

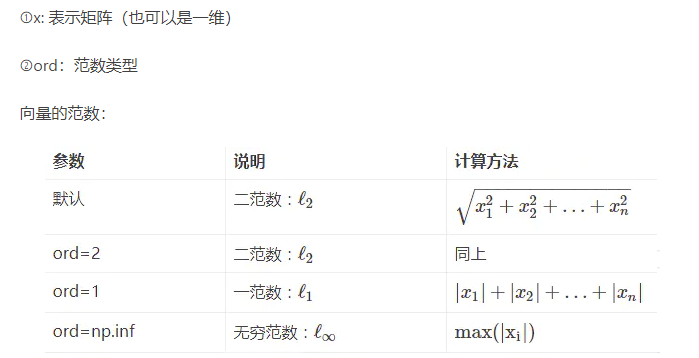
norm表示范数，函数参数如下：

x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)  　

 

import numpy as np 
from numpy import linalg

x = np.array([3,4])
# 向量范数（默认参数ord=None，axis=None，keepdims=False）
print('L1=
',linalg.norm(x,ord=1))
print('L2=
',linalg.norm(x))
print('L∞=
',linalg.norm(x,ord=np.inf))

y = np.array([
        [0,3,4],
        [1,6,4]])

# 矩阵范数
print('矩阵1范数=
',linalg.norm(y,ord=1))
print('矩阵2范数=
',linalg.norm(y))
print('矩阵∞范数=
',linalg.norm(y,ord=np.inf))

print('矩阵每个行向量求向量的1范数：',linalg.norm(y,ord=1,axis=1,keepdims=True)) 

L1=
 7.0
L2=
 5.0
L∞=
 4.0
矩阵1范数=
 9.0
矩阵2范数=
 8.831760866327848
矩阵∞范数=
 11.0
矩阵每个行向量求向量的1范数： [[ 7.]
 [11.]]

 0x01 闵可夫斯基距离

 

0x02 欧式距离

代码实现：

import numpy as np 
vector1 = np.mat([1,2,3])
vector2 = np.mat([4,5,6])
print('欧氏距离:
',np.sqrt((vector1-vector2)*(vector1-vector2).T))

欧氏距离:
 [[5.19615242]]

0x03 曼哈顿距离

 代码实现：

import numpy as np 
vector1 = np.mat([1,2,3])
vector2 = np.mat([4,5,6])
print('曼哈顿距离:
',np.sum(np.abs(vector1-vector2)))

曼哈顿距离:
 9

0x04 切比雪夫距离

 代码实现：

import numpy as np 
vector1 = np.mat([1,2,3])
vector2 = np.mat([4,7,5])
print('切比雪夫距离:
',np.abs(vector1-vector2).max())

切比雪夫距离:
 5

0x05 夹角余弦

 代码实现：

import numpy as np 
from numpy import linalg
#方法1
vector1 = np.mat([1,2,3])
vector2 = np.mat([4,7,5])
cosV12 = np.dot(vector1,vector2.T)/(linalg.norm(vector1)*linalg.norm(vector2))
print('夹角余弦:
',cosV12)
#方法2
vector1 = [1,2,3]
vector2 = [4,7,5]
cosV12 = np.dot(vector1,vector2)/(linalg.norm(vector1)*linalg.norm(vector2))
print('夹角余弦:
',cosV12)
#区别：方法1向量为matrix格式，方法2为list

夹角余弦:
 [[0.92966968]]

0x06 汉明距离

汉明距离的定义：两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
应用：信息编码（为了增强容错性，应使得编码间的最小汉明距离尽可能大）。

import numpy as np 
from numpy import linalg
'''
np.nonzero的用法，返回非零元素的位置(某行某列)
vector = np.mat([[1,1,0,1,0,1,0,0,1],
                 [1,0,1,1,0,1,0,0,1]])
smstr = np.nonzero(vector)
print(np.array(smstr))
print(np.array(smstr).ndim)
print(smstr)
'''
vector1 = np.mat([1,1,0,1,0,1,0,0,1])
vector2 = np.mat([0,1,1,0,0,0,1,1,1])
smstr = np.nonzero(vector1-vector2)
#print(np.array(smstr))
#print(np.array(smstr).ndim)
print('汉明距离:
',np.shape(smstr[0])[0])

'''
[[0 0 0 0 0 1 1 1 1 1]
 [0 1 3 5 8 0 2 3 5 8]]
2
 (array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1], dtype=int64), array([0, 1, 3, 5, 8, 0, 2, 3, 5, 8], dtype=int64))
'''
汉明距离:
 6

0x07 杰卡德相似系数

 

 代码实现：

import numpy as np 
import scipy.spatial.distance as dist
matV = np.mat([[1,1,0,1,0,1,0,0,1],
              [0,1,1,0,0,0,1,1,1]])
print('杰卡德距离:
',dist.pdist(matV,'jaccard'))

杰卡德距离:
 [0.75]

0x08 相关系数和协方差

 代码实现：

import numpy as np 
from numpy import linalg

featuremat = np.mat([np.random.randint(0,9,3),
                     np.random.randint(0,9,3),
                     np.random.randint(0,9,3)])
print(featuremat)
# 计算均值
mv1 = np.mean(featuremat[0])
mv2 = np.mean(featuremat[1])
# 计算两列标准差
dv1 = np.std(featuremat[0])
dv2 = np.std(featuremat[1])
# 相关系数和相关距离
corrf = np.mean(np.multiply(featuremat[0]-mv1,featuremat[1]-mv2)/(dv1*dv2))
print('二维相关系数',corrf)
print('相关距离=',1-corrf)
print('***'*15)
# 使用numpy进行相关系数计算
print('多维相关系数=
',np.corrcoef(featuremat))
# 使用numpy进行协方差矩阵计算
print('多维协方差=
',np.cov(featuremat))

[[4 2 3]
 [6 6 7]
 [4 5 0]]
二维相关系数 0.0
相关距离= 1.0
*********************************************
多维相关系数=
 [[ 1.          0.         -0.18898224]
 [ 0.          1.         -0.98198051]
 [-0.18898224 -0.98198051  1.        ]]
多维协方差=
 [[ 1.          0.         -0.5       ]
 [ 0.          0.33333333 -1.5       ]
 [-0.5        -1.5         7.        ]]

0x09 马氏距离

 代码实现：

import numpy as np 
from numpy import linalg

featuremat = np.mat([np.random.randint(0,9,3),
                     np.random.randint(0,9,3)])

print(featuremat)

covinv = linalg.inv(np.cov(featuremat))
tp = featuremat.T[0]-featuremat.T[1]
distma = np.sqrt(np.dot(np.dot(tp,covinv),tp.T))
print(distma)

[[4 2 8]
 [4 2 7]]
[[2.]]

0x0A 参考

参考网站：

https://www.jianshu.com/p/45417c05574c

https://www.cnblogs.com/wj-1314/p/10244807.html

https://www.cnblogs.com/endlesscoding/p/10033527.html

https://www.cnblogs.com/zongfa/p/8745853.html

参考书籍：《python科学计算》《机器学习算法原理与编程实践》

0x0B 转载