圆排列问题
1. 问题
给定n个圆的半径序列,将它们放到矩形框中,各圆与矩形底边相切,求具有最小排列长度的原序列。
2. 解析
圆排列问题的解空间是一颗排列树。按照回溯法搜索排列树的算法框架,设开始时r=[r1,r2,…,rn]是所给的n个圆的半径,则相应的排列树由r[1:n]的所有排列构成。
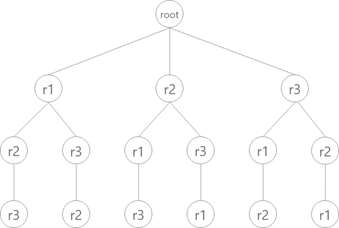
图 1 当n=3时的解空间
calx(t)用于计算第t个圆的圆心的横坐标。

图 2 几种计算圆心坐标的情况
当我们求第t个圆的圆心的时候,他可能与前t-1个圆中的每一个圆相切,所以需要遍历前t-1个圆求出第t个圆的圆心横坐标。初始化的时候,第一个圆的圆心横坐标为0。
以图2为例,假设圆a的横坐标为x[a],半径为r[a],圆b的半径为r[b]。
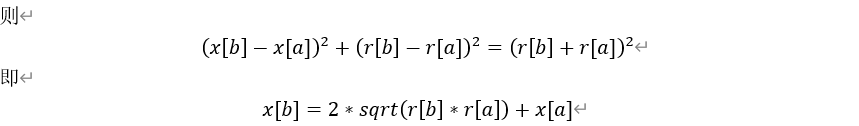
当我们遍历到解空间树的叶子节点时,遍历该解序列中每一个圆的左边界(x[i]-r[i])和右边界(x[i]+r[i]),取所有圆的最小左边界left,最大右边界right。两者相加即为最小圆排列长度。然后更新答案数组。
在dfs中,加入剪枝,若当前圆t的坐标x[t]+r[t]+r[1]>=最小圆排列长度,就不再继续遍历这个解序列了,因为这个解序列的圆排列长度已经大于当前所求的最小圆排列长度,已经不是最优解,没有继续遍历的必要。
3. 设计
1 #include<math.h> 2 #include<stdio.h> 3 #include<algorithm> 4 using namespace std; 5 6 const int N = 100; 7 const int inf = 0x3f3f3f3f; 8 double minn = inf; //最小圆排列长度 9 int n; 10 double x[N], r[N]; //分别为每个圆心横坐标,每个圆半径 11 double res[N]; //最小圆排列的半径顺序 12 13 double calx(int t) { //计算第t个圆的圆心坐标 14 double temp = 0; 15 for (int j = 1; j < t; ++j) { 16 double now = x[j] + 2.0 * sqrt(r[t] * r[j]); //判断与他之前的所有圆相切的情况 17 if (now > temp) //取所求圆心的最小值 18 temp = now; 19 } 20 return temp; 21 } 22 void compute() { 23 double left = inf, right = 0; //left是左边界,right是有边界 24 for (int i = 1; i <= n; ++i) { 25 if (x[i] - r[i] < left) 26 left = x[i] - r[i]; 27 if (x[i] + r[i] > right) 28 right = x[i] + r[i]; 29 } 30 if (right - left < minn) { 31 minn = right - left; 32 for (int i = 1; i <= n; ++i) 33 res[i] = r[i]; 34 } 35 } 36 void dfs(int t) { 37 if (t == n + 1) { 38 compute(); 39 } 40 else { 41 for (int j = t; j <= n; ++j) { 42 swap(r[t], r[j]); 43 double now = calx(t); 44 if (now + r[t] + r[1] < minn) { 45 x[t] = now; 46 dfs(t + 1); 47 } 48 swap(r[t], r[j]); //还原 49 } 50 } 51 } 52 int main() { 53 scanf("%d",&n); 54 for (int i = 1; i <= n; ++i)scanf("%lf", &r[i]); 55 dfs(1); 56 printf("最小圆排列长度为:%.4f ", minn); 57 printf("最小圆排列的顺序对应的半径分别为: "); 58 for (int i = 1; i <= n; ++i) { 59 if (i != 1)printf(" "); 60 printf("%.4f", res[i]); 61 } 62 return 0; 63 }
4. 分析
该算法在最坏情况下会遍历所有的解空间序列,此时的时间复杂度为O(n!)。
由于每次都需要计算圆排列长度,此时的时间复杂度为O(n)。
综上,该算法的时间复杂度为O((n+1)!)。
5. 源码
https://github.com/JayShao-Xie/algorithm-work/blob/master/Circle.cpp