题意:
给定一副n*m的格子图, 问从左上角的点开始往右下角滑,碰到墙壁就反弹, 碰到角落就停止, 问恰好经过一次的格子有多少个。
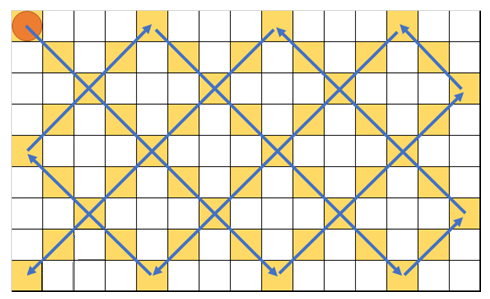
如图,恰好经过一次的格子有39个。
分析:
首先要引入两个概念, “路径长”,“格子数”。
路径长指的是整段路程的长度,如果走过同一个格子两次那么就算是2步。
格子数指的是整段路程经过的格子。
如果一个图是9*9(形如n*n)的, 那么就是从左上角一直到右下角, 走过的“路径长”恰好等于“格子数”,没有任何的格子被走过两次。
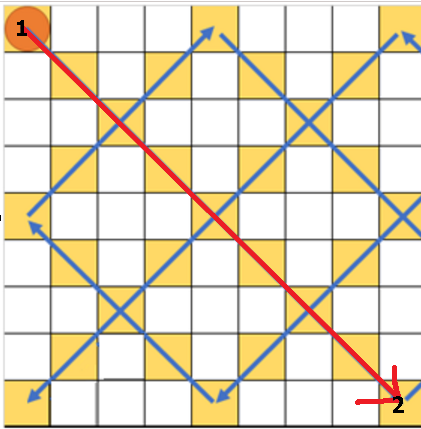
但对于一幅9 * 15这样不规则的图,“格子数”为“48”,“路径长”为57。
如果把格子都平移成一条直线的话, 那么有一些格子就会存在“共用”。上图中1~9号都成为“共用点”,其中“3、6、9”为行共用,“2、4、5、7、8、10”为列共用点,1和11分别给起点和终点。
只考虑1 - 2 - 3 - 4 - 5 - 6 这条连线, 如果把他们平移成行的话, 那么只有15 + 14的“路径长” , 并非两行15*2 =30 “路径长”。 因为3号顶点是这两行共用的, 不能单独算。整幅图而言,因为行共用点有3个, 所以最后如果都算行平移的话会有15 + (15-1)*3 = 57“路径长”, 如果都算列平移同样会有9 + (9-1)*6 = 57“路径长”。

那么我们考虑将一个n*m的“路径长”,放大成最小倍数使其变为没有“共用点”的 a*a图便于我们运算。 那么a应该等于 (lcm(n-1,m-1)), 行放大倍数为a/n, 列放大倍数为a/m。
注意最后再加上1,因为“共用点总比边数少1”,换而言之就是有一条边是没有公共点的, 我们都按“lcm(n-1,m-1)”倍数去放大的话就会少算了一格。
这样我们就能得出“路径长”的公式为 lcm(n-1,m-1) + 1。
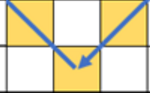
考虑2*3的格子, 现在行公用点其实是0, 格子共有3*1 = 3 个, 竖公共点有1个, 格子共有2+(2-1)*1 = 3 个。
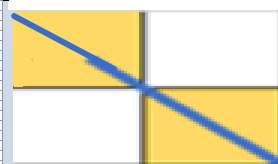
接下来我们处理,“路径长” 和“格子数”的关系。
由图可得, 因为有些格子走了2次(至多2次),所以"路径长”算多了一次。
其实 “路径长” =“走过一次格子数” * 1 + “走过两次格子数” * 2。
那么我们既然要求的是“走过一次的格子数”, 而且“路径长“也算出来了, 就可以得出。
"路径长" - “走过两次格子数”*2 = “走过一次格子数” (即都视为走过两次的, 减掉路径就知道走过一次格子有多少)。
所以问题就转化为求“格子数”的问题了,
而且发现没有, 9 * 15的图中,按行算只有 4 , 按列算只有7, 恰好是 lcm(8,14) = 56
56/ 8 = 7和 56 / 14 = 4 的结果。
这就说明, 我们用“共用点”计算的行列,是和我们放大的倍数有关系的。
那些走过两次的点, 其实就是行列的交叉点, 推了一下大概的公式,大概就是

#include<bits/stdc++.h> using namespace std; long long gcd(long long a, long long b){ return b == 0 ? a : gcd(b,a%b); } long long lcm(long long a, long long b){ return a*b/gcd(a,b); } int main(){ long long n , m; while(~scanf("%lld %lld", &n, &m)){ long long l = lcm(n-1,m-1); long long a = l/(m-1) , b = l/(n-1); printf("%lld ",l - a*b + a + b); } return 0; }