树状数组
简介
为什么需要树状数组?
举一个简单的例子,有一个数组[ 9 , 3 , 2 , 5 , 7 ],当我们需要计算数组任意X~X+N项元素的和,若采用传统方式,则需要从X开始一路加到X+N,需要的时间复杂度o(n)。
若要进一步优化我们可以求出含有对应位置前n项和的数组,例如上述数组对应结果为T[9 , 12 , 14 , 19 , 26],若要再求X~X+N个元素的和,只需计算T[X+N] - T[X]即可,但问题是当在数组某个位置重新插入一个元素时,需要将其位置后面的所有元素都更新,时间复杂度仍是O(N)
这个时候树状数组就出现了,树状数组的插入和查询任意n项和的时间复杂度都是o(log n)
以[1 , 2 , 3 , 4 , 5 , 6 , 7 , 8]为节点的一颗完整树状数组如下图
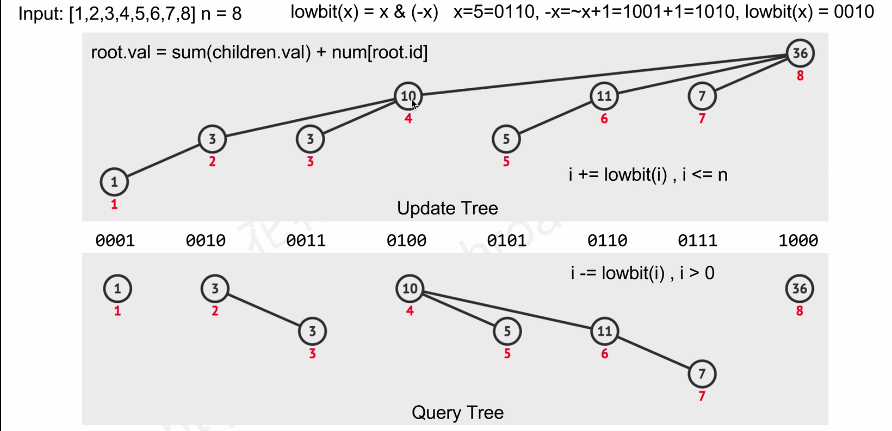
树状数组每个节点的父节点为pos += lowbit(i),i<n
-
lowbit是指一个整数的二进制表示,从后往前数一直到第一个1所代表的大小
例如 3 = 011 那么3的lowbit即为1
6 =0110 那么6的lowbit为 2
关于lowbit有一个很简单的求法那就是( X&~X )
插入或更新元素
当我们需要插入一个元素时,从这个元素开始,依次更新这个节点一直到树根中所有元素
以2号节点元素加上5为例,初始化pos = 2
1.更新2号元素 3+5=8
2.pos+=lowbit(2) pos = 4
3.更新4号元素 10+5=15
4.pos+=lowbit(4) pos = 8
5.更新8号元素 36+5=41
6.8号已到达数组末尾,更新结束
查询
当我们需要查询某位置对应的前n项和,则依次从对应位置开始依次访问直到pos==0
以节点5前n项和为例,先初始化ans=0,pos = 5
1.ans+=t[pos] pos = 5 ans = 5
2.pos -= lowbit(5) pos = 4 ans = 5
3.ans += t[pos] pos = 4 ans = 15
4.pos -= lowbit(5) pos = 0 ans = 15
前5项和为15