Hdoj 1253

原题链接

描述

Ignatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会.

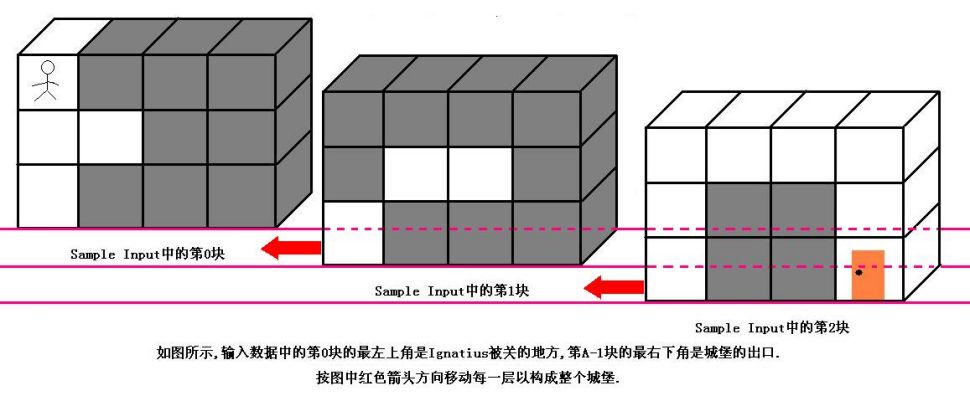
魔王住在一个城堡里,城堡是一个ABC的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,现在知道魔王将在T分钟后回到城堡,Ignatius每分钟能从一个坐标走到相邻的六个坐标中的其中一个.现在给你城堡的地图,请你计算出Ignatius能否在魔王回来前离开城堡(只要走到出口就算离开城堡,如果走到出口的时候魔王刚好回来也算逃亡成功),如果可以请输出需要多少分钟才能离开,如果不能则输出-1.

输入

输入数据的第一行是一个正整数K,表明测试数据的数量.每组测试数据的第一行是四个正整数A,B,C和T(1<=A,B,C<=50,1<=T<=1000),它们分别代表城堡的大小和魔王回来的时间.然后是A块输入数据(先是第0块,然后是第1块,第2块......),每块输入数据有B行,每行有C个正整数,代表迷宫的布局,其中0代表路,1代表墙.(如果对输入描述不清楚,可以参考Sample Input中的迷宫描述,它表示的就是上图中的迷宫)
特别注意:本题的测试数据非常大,请使用scanf输入,我不能保证使用cin能不超时.在本OJ上请使用Visual C++提交.

输出

对于每组测试数据,如果Ignatius能够在魔王回来前离开城堡,那么请输出他最少需要多少分钟,否则输出-1.

样例输入

1
3 3 4 20
0 1 1 1
0 0 1 1
0 1 1 1
1 1 1 1
1 0 0 1
0 1 1 1
0 0 0 0
0 1 1 0
0 1 1 0

样例输出

11

思路

BFS搜最短路就好，二维拓展到三维。

代码

#include <bits/stdc++.h>
using namespace std;

int a, b, c, t;
int dst[51][51][51], vst[51][51][51];

int dirx[6] = {-1,1,0,0,0,0};
int diry[6] = {0,0,1,-1,0,0};
int dirz[6] = {0,0,0,0,-1,1};

struct state
{
	int x, y, z;
	int count;
	state() {count = 0;}
	bool judge()
	{
		if(x == a-1 && y == b-1 && z == c-1)
			return true;
		return false;
	}
	void putter(int xx, int yy, int zz, int cc)
	{
		x = xx; y = yy; z = zz; count = cc;
	}
};

void init()
{
	memset(vst, 0, sizeof(vst));
	memset(dst, 0, sizeof(dst));
}

void bfs(state u)
{
	queue<state> q;
	q.push(u);
	while(!q.empty())
	{
		u = q.front(); q.pop();
		if(u.judge())
		{
			if(u.count <= t)
				printf("%d
", u.count);
			else printf("-1
");
			return;
		}
		for(int i = 0; i < 6; i++)
		{
			int xx = u.x + dirx[i];
			int yy = u.y + diry[i];
			int zz = u.z + dirz[i];
			int step = u.count + 1;
			if(xx < 0 || xx >= a || yy < 0 || yy >= b || zz < 0 || zz >= c) continue;
			if(vst[xx][yy][zz] || dst[xx][yy][zz]) continue;
			vst[xx][yy][zz] = 1;
			state v;
			v.putter(xx, yy, zz, step);
			q.push(v);
		}
	}
	printf("-1
");
}

int main()
{
	int T; scanf("%d", &T);
	while(T--)
	{
		init();
		scanf("%d%d%d%d", &a, &b, &c, &t);
		for(int i = 0; i < a; i++)
			for(int j = 0; j < b; j++)
				for(int k = 0; k < c; k++)
					scanf("%d", &dst[i][j][k]);
		state st;
		st.putter(0, 0, 0, 0);
		vst[0][0][0] = 1;
		bfs(st);
	}
    return 0;
}