Hanoi塔

Hanoi塔问题是源于印度一个古老传说的益智玩具。设a,b,c是三个塔座，开始时，在塔座a上有一叠共n个圆盘，这些圆盘自上而下，由大到小叠在一起，各圆盘的编号为1,2,3，...，n。现要求将塔座a上的这一叠圆盘移动到塔座b上，并仍按从到到小的顺序叠置。再移动圆盘时应该遵守以下移动规则：

规则一：每次只能移动一个圆盘。

规则二：不允许将较大的圆盘压在较小的圆盘上面。

规则三：在满足规则一、规则二的情况下，可将圆盘移动到啊a,b,c中任一塔座上。

如图为一Hanoi塔问题的移动步骤：

a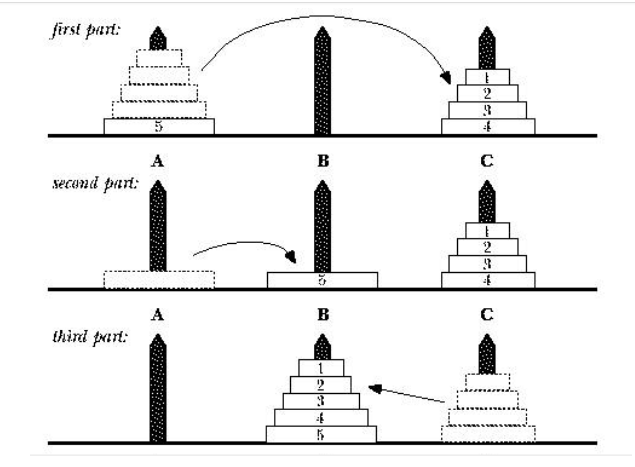

圆盘总数为n，当n=1时，只要将编号为1的圆盘从塔座a直接移动到塔座b。当n>1时，需要利用塔座c作为辅助，将n-1个较小的圆盘依照移动规则从塔座a移动至塔座c，然后将最大的圆盘从塔座a移动至塔座b，再将n-1个圆盘从塔座c移动至塔座b，T(n)=2^(n-1)-1。由于n-1个圆盘以同样的方式移动了两次，可以利用递归方法来解决。这个就是典型的Hanoi塔递归问题。

 public static void hanoi(int n,int a,int b,int c){
        if(n>0){
            hanoi(n-1,a,c,b);
            move(a,b);
            hanoi(n-1,c,b,a);
        }
    }

如果将三个塔座a,b,c改为四个塔座a,b,c,d，利用分治法则和归纳法分成两个小规模问题。

T(n)来表示最小步数，可以知道T（1）=1，T（2）=3，当n>=3时，假设已经输出T(1),T(2),…,T(n-1),则T(n)可以这样计算：

for i=1;i<n;i++

一：先从塔座a移动i个圆盘到塔座d（b,c）,塔座b，c作为辅助，移动步数为T(i)。

二：剩下的n-i个圆盘只可以在三个塔座之间移动，利用Hanoi函数将其由塔座a移动至塔座，塔座c作为辅助，移动步数为T(n-i)=2^(n-i)-1。

三：再将塔座d中的i个圆盘移动至塔座b，塔座c,a作为辅助(与步一移动方式相同)移动步数为T(i)。

public class Han {

    //创建一个静态数组用于存储移动的圆盘的最小步数
    static int[] a=new int [65];

    //创建一个静态数组用于存储先移动的圆盘的个数
    static int[] s=new int [65];

    public static void step() {
        a[0] = 0;
        a[1] = 1;
        a[2] = 3;

        //先移动圆盘个数的循环
        for (int n = 3; n <= 64; n++) {
            double min = 200000;
            double temp = 0;
            int temp2 = 0;

            //一个一个移动计算步数和圆盘个数
            for (int i = 1; i < n; i++) {
                temp = 2 * a[i] + Math.pow(2, n - i) - 1;
                if (temp < min) {
                    min = temp;//计算出移动总步数并赋值
                    temp2 = i;//计算出先移动圆盘数并赋值
                }
                a[n] = (int) temp;
                s[n] = temp2;
            }
        }
    }

public static void hanoi4(int n,int a,int b,int c,int d,int []s){
        if(n>=3){
            hanoi4(s[n],a,b,c,d,s);
            hanoi(n-s[n],a,c,b);
            hanoi4(s[n],d,a,b,c,s);
        }else{
            if(n==1){
                move(a,b);
            }
            if(n==2){
                hanoi(2,a,c,b);
            }
        }
    }

示例：

在Hanoi塔问题中如果塔的个数变为a,b,c,d四个，现要将n个圆盘从a全部移动到d，移动规则不变，编写移动步数最小的方案和具体的移动过程（只考虑n<=64），并演示当n=9时的情形。

package jihe;

/**
 * author Gsan
 */
public class Han {

    //创建一个静态数组用于存储移动的圆盘的最小步数
    static int[] a=new int [65];

    //创建一个静态数组用于存储先移动的圆盘的个数
    static int[] s=new int [65];

    public static void step() {
        a[0] = 0;
        a[1] = 1;
        a[2] = 3;

        //先移动圆盘个数的循环
        for (int n = 3; n <= 64; n++) {
            double min = 200000;
            double temp = 0;
            int temp2 = 0;

            //一个一个移动计算步数和圆盘个数
            for (int i = 1; i < n; i++) {
                temp = 2 * a[i] + Math.pow(2, n - i) - 1;
                if (temp < min) {
                    min = temp;//计算出移动总步数并赋值
                    temp2 = i;//计算出先移动圆盘数并赋值
                }
                a[n] = (int) temp;
                s[n] = temp2;
            }
        }
    }

    public static void hanoi(int n,int a,int b,int c){
        if(n>0){
            hanoi(n-1,a,c,b);
            move(a,b);
            hanoi(n-1,c,b,a);
        }
    }

    public static void move(int a,int b){
        System.out.println("move"+a+"to"+b);
    }

    public static void hanoi4(int n,int a,int b,int c,int d,int []s){
        if(n>=3){
            hanoi4(s[n],a,b,c,d,s);
            hanoi(n-s[n],a,c,b);
            hanoi4(s[n],d,a,b,c,s);
        }else{
            if(n==1){
                move(a,b);
            }
            if(n==2){
                hanoi(2,a,c,b);
            }
        }
    }

    public static void main(String[] args) {

        int n=9;
        step();
        hanoi4(n,1,2,3,4,s);

        System.out.println("9个圆盘移动的最小步数为："+a[n]);
    }

}

运行结果：