维护动态区间的中位数

问题描述

依次读入一个整数序列，每当已经读入的整数个数为奇数时，输出已读入的整数构成的序列的中位数。详细内容

sort

最朴素写法，每到奇数时位将前面所有数据排序，找到中位数
每次sort是(o(nlog_n))，一组数据需要sort (frac{n}{2})次,所以复杂度为(o(n^2log_n))

#include <iostream>
#include <algorithm>

using namespace std;

const int M = 10010;

int a[M];

int main()
{
    int p;
    cin >> p;
    while (p --)
    {
        int n, m;
        cin >> n >> m;
        cout << n << ' ' << (m + 1 >> 1) << endl;

        int cnt = 0;
        for (int i = 1; i <= m; ++ i)
        {
            cin >> a[i];
            if (i % 2 != 0) 
            {
                sort(a + 1, a + i + 1);
                cout << a[1 + i >> 1] << ' ';
                if (++ cnt % 10 == 0) cout << endl;   
            }
        }

        if (cnt % 10) cout << endl; // 解决最后一行数据不够10个，上方未输出空行，会导致下面组的格式出问题
    }

    return 0;
}

快速选择

寻找中位数，上述做法采用(O(nlog_n))的快速排序，也可以采用O(n)的快速选择
所以每组的复杂度就变为了(o(n^2))

#include <iostream>
#include <algorithm>

using namespace std;

const int M = 10010;

int a[M];

int qsort(int a[], int l, int r, int k)
{
    if (l >= r) return a[l];

    int x = a[l + r >> 1], i = l - 1, j = r + 1;
    while (i < j)
    {
        while (a[++ i] < x);
        while (a[-- j] > x);
        if (i < j) swap(a[i], a[j]);
    }

    int sl = j - l + 1;
    if (k <= sl) return qsort(a, l, j, k);
    return qsort(a, j + 1, r, k - sl);
}
int main()
{
    int p;
    cin >> p;
    while (p --)
    {
        int n, m;
        cin >> n >> m;
        cout << n << ' ' << (m + 1 >> 1) << endl;

        int cnt = 0;
        for (int i = 1; i <= m; ++ i)
        {
            cin >> a[i];
            if (i % 2 != 0) 
            {
                cout << qsort(a, 1, i, 1 + i >> 1) << ' ';
                if (++ cnt % 10 == 0) cout << endl;   
            }
        }

        if (cnt % 10) cout << endl; // 解决最后一行数据不够10个，上方未输出空行，会导致下面组的格式出问题
    }

    return 0;
}

对顶堆

应用场景
维护动态区间的中位数

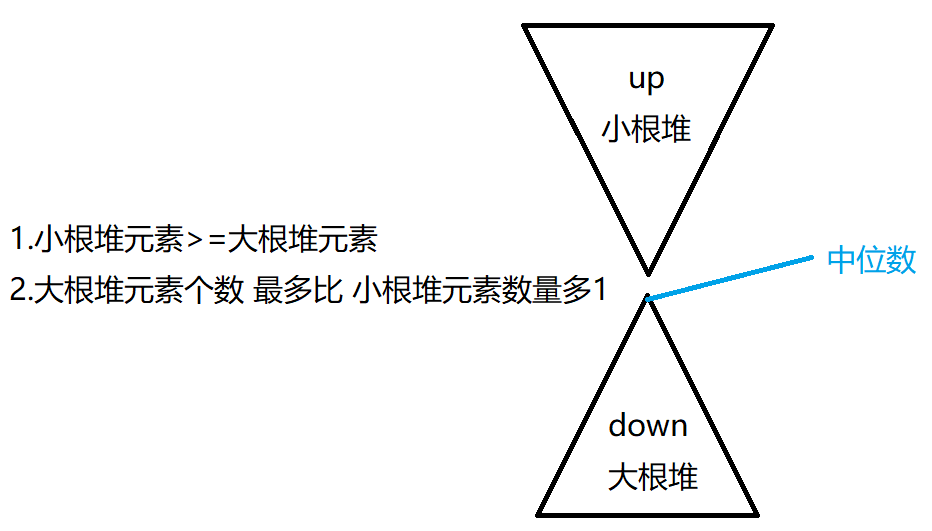
小根堆始终维护大于大根堆堆顶元素的元素，大根堆维护小于大根堆堆顶元素的元素，由于我们保证大根堆元素个数最多比小根堆元素个数多1，所以在奇数个元素的情况下，两个堆的元素数量不会相等，一定是相差1，大根堆堆顶元素恰好位于中位数的位置，每个数据插入堆中是(O(log_n))的，所以每组的时间复杂度为(O(nlog_n))
之所以能够想到这样的解法，是因为我们确定中位数其实并不需要保证其左右两侧数据的有序性，只要左侧数据都小，右侧数据都大即可，使用两个堆恰好能够维护这种性质

#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

int main()
{
    int p;
    cin >> p;
    while (p --)
    {
        int n, m;
        cin >> n >> m;
        cout << n << ' ' << (m + 1 >> 1) << endl;

        priority_queue<int> down; // 下方的大根堆
        priority_queue<int, vector<int>, greater<int>> up; // 上方的小根堆

        int cnt = 0;
        for (int i = 1; i <= m; ++ i)
        {
            int x;
            cin >> x;

            if (down.empty() || x < down.top()) down.push(x); // 这里用<或<=均可，因为我们只需要保证中位数的相对位置正确即可
            else up.push(x);

            /**
             * 这里只是规定了down的大小比size的大小大1，这样中位数一定在down中
             * 如果没有明确规定哪个堆中数据更多，而只是保证两者大小的差的绝对值不大于1，那么中位数出现在size更大的堆中，
             * 虽然这样同样可以得出结论，但由于没有明确规定中位数到底出现在哪里，所以代码实现时判断条件要更多一些
             */
            if (down.size() > up.size() + 1) up.push(down.top()), down.pop();
            /**
             * 按照理论，需要保证大根堆down的个数使用比小根堆的个数大一
             * 即合法状态为up.size() = down.size() - 1，所以当up.size() >= down.size()时就需要调整，可这里没有=为什么也能ac
             * 原因在于题目中规定了奇数个数时才会选择中位数，此时up和down中总数为奇数，两者size不可能相等，所以>时才调整也能保证到奇数个时能够得到正确结果
             */
            if (up.size() >= down.size()) down.push(up.top()), up.pop();

             if (i % 2 != 0) 
            {
                cout << down.top() << ' ';
                if (++ cnt % 10 == 0) cout << endl;   
            }
        }

        if (cnt % 10) cout << endl; // 解决最后一行数据不够10个，上方未输出空行，会导致下面组的格式出问题
    }

    return 0;
}