【了解】贝塞尔曲线

目录

• 曲线美
• 原理
  • 命名：贝塞尔曲线（Bézier curve）
  • 曲线绘制过程
  • 数学知识(二阶贝塞尔曲线为例)
  • 个人理解
• 浏览器中如何绘制
  • css
    • transition-timing-function：立方贝塞尔曲线（三阶贝塞尔曲线）
  • canvas
    • 二阶贝塞尔曲线：quadraticCurveTo
    • 三阶贝塞尔曲线：bezierCurveTo
  • svg
    • 二阶贝塞尔曲线：Q/q = quadratic Bézier curve
    • 三阶贝塞尔曲线：C/c = curveto
    • 组合：
  • webGl
  • css + js
    • background-image: paint(worklet-name);
  • css, canvas, svg 三阶贝塞尔总结
  • 高阶
• 扩展
• 应用
  • 1. 小球抛物线运动
  • 2. 水波图
  • 3. 如何根据已知的点数据绘制出一条平滑的曲线？

曲线美

• qq 浏览器宣传页
• 曲线图
• 水波图
• 桑基图

原理

命名：贝塞尔曲线（Bézier curve）

组成：由起点、终点、控制点组成。

说明：其中控制点的个数可以是0-n, 0个控制点的时候为一阶贝塞尔曲线（一条直线），1个控制点的时候为二阶贝塞尔曲线，以此类推。

重要性：是计算机图形学中相当重要的参数曲线。

前身：伯恩斯坦多项式，德卡斯特里奥算法

由来：由法国工程师（数学家）皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。

出发点：只需要很少的控制点，就可以绘制出一条平滑复杂的曲线。

曲线绘制过程

• 一阶贝塞尔曲线

  

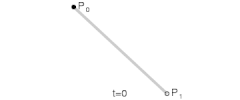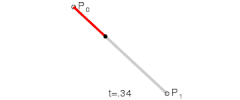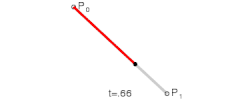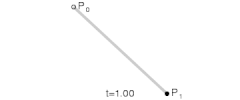
• 二阶贝塞尔曲线

  

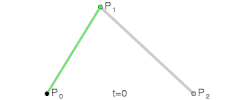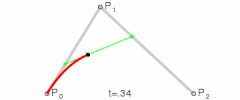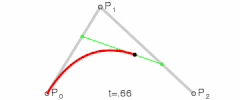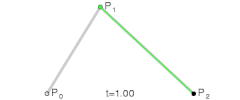
• 三阶贝塞尔曲线

  

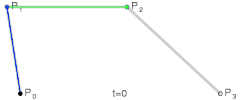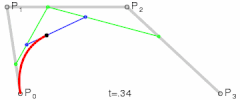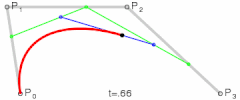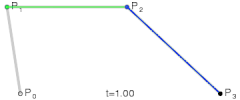
• 四阶贝塞尔曲线

  

• 高阶阶贝塞尔曲线

  

说明：在p0p1、p1p2、p2p3等等的起点到控制点再到终点的连线中，每段连线都被分割成了两部分（仔细看动图中的黑色、绿色、蓝色圆点），各段连线中两部分的比值都是相同的，比值范围是0到1，而这个比值就是t

在线绘制，来源于 h5 canvas n 阶贝塞尔曲线

数学知识(二阶贝塞尔曲线为例)

• 步骤一：在平面内选3个不同线的点并且依次用线段连接

  

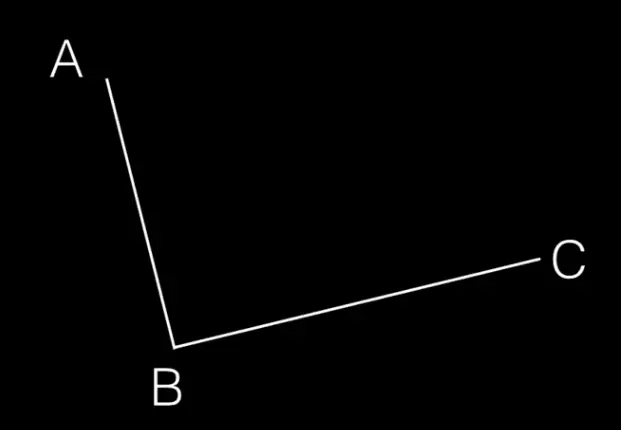
• 步骤二：在AB和BC线段上找出点D和点E，使得 AD/AB = BE/BC

  

• 步骤三：连接DE，在DE上寻找点F，F点需要满足：DF/DE = AD/AB = BE/BC

  

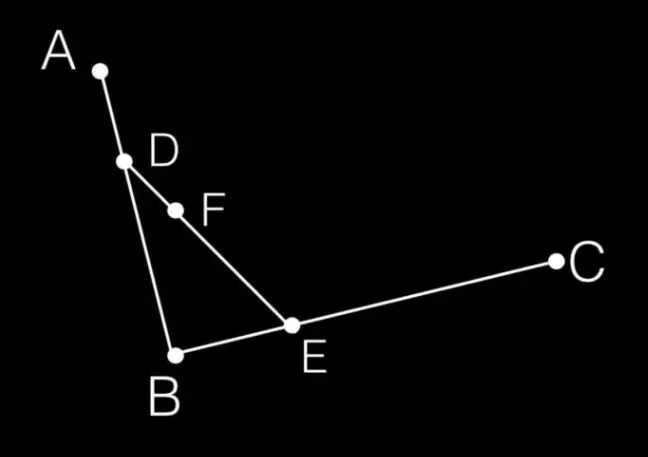
• 步骤四：最最重要的!

  • 上面三步是在讲如何确定F点，DF/DE = AD/AB = BE/BC = t
  • 当 t 从 0-1 变化时，逆推出的所有 F 点连接起来，就绘制出了一条曲线
  

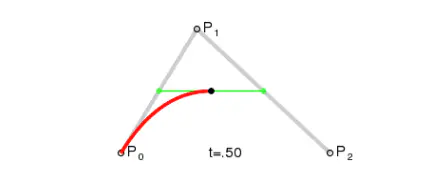
  P0 == A；P1 == B；P2 == C

• 公式推导

  P点为已知点，B点为最终所求的点(上面图所示的F点)。

  • 一阶贝塞尔：B(t) = P0(1-t) + p1t

  • 二阶贝塞尔：B(t) = P0(1-t)² + 2P1t(1-t) + P2t²

  • 三阶贝塞尔：B(t) = P0(1-t)³ + 3P1t(1-t)² + 3P2t²(1-t) + P3t³

  • n阶贝塞尔

    

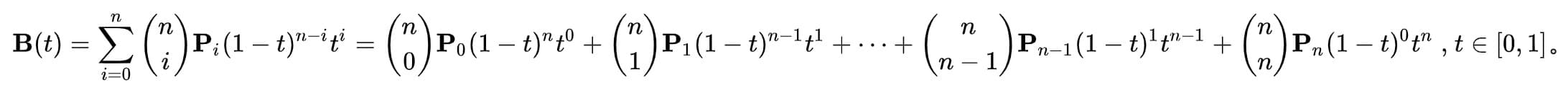
个人理解

• 一阶贝塞尔曲线：一根直线
• 二阶至n阶贝塞尔曲线：曲线
• n 阶贝塞尔曲线由 n+1 个点控制
• 三阶贝塞尔曲线应用最广
• 任何高阶贝塞尔曲线，都可通过多个低阶贝塞尔曲线组合而成
• 二阶只能绘制出一个弯曲的弧度，若要再加一个弯曲的弧度，方案有2：
  • 增加一阶，使用高阶
  • 两个二阶重复

浏览器中如何绘制

css

transition-timing-function：立方贝塞尔曲线（三阶贝塞尔曲线）

cubic-bezier(x1, y1, x2, y2)

• x1,y1 第一个控制点
• x2,y2 第二个控制点
• 默认起点 0,0 终点 1,1

transition: all 1s cubic-bezier(.25,.1,.25,1)

• css 贝塞尔曲线可视化

canvas

二阶贝塞尔曲线：quadraticCurveTo

说明：quadratic： 二次方

语法：

// cpx,cpy 控制点
// x,y 结束点
context.quadraticCurveTo(cpx,cpy,x,y)

示例:

const canvas = document.getElementById("myCanvas");
const ctx = canvas.getContext("2d");
ctx.beginPath();
ctx.moveTo(20,20);
ctx.quadraticCurveTo(20,100, 200,20);
ctx.stroke();

示例说明：

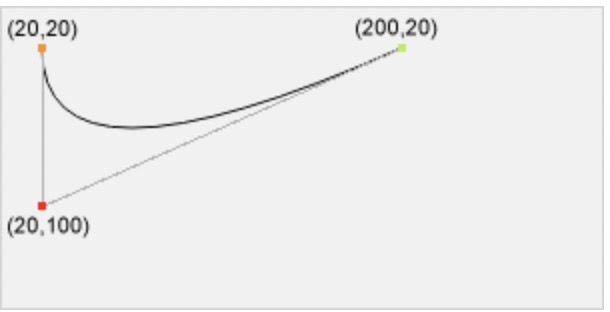
三阶贝塞尔曲线：bezierCurveTo

语法：

// cp1x,cp1y 控制点1
// cp2x,cp2y 控制点
// x,y 结束点
// x,y 结束点
context.bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y);

示例：

const canvas = document.getElementById("myCanvas");
const ctx = canvas.getContext("2d");
ctx.beginPath();
ctx.moveTo(20,20);
ctx.bezierCurveTo(20,100, 200,100, 200,20);
ctx.stroke();

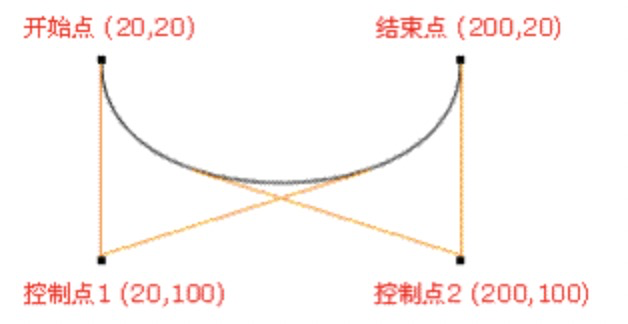
svg

利用 svg 的 path 标签绘制。

path 标签的 d 属性中的 M 表示：moveTo

大写表示绝对定位，小写表示相对定位。

二阶贝塞尔曲线：Q/q = quadratic Bézier curve

示例：M：起点，Q：两个点

<svg xmlns="http://www.w3.org/2000/svg" version="1.1" width="190px" height="160px">
  <path d="M20 20 Q 20,100, 200,20" stroke="orange" stroke-width="3" fill="none"/>
</svg>

三阶贝塞尔曲线：C/c = curveto

示例：M：起点，C：三个点

<svg xmlns="http://www.w3.org/2000/svg" version="1.1" width="190px" height="160px">
  <path d="M20 20 C20 100, 200 100, 200 20" stroke="orange" stroke-width="3" fill="none"/>
</svg>

组合：

• Q(quadratic Bézier curve) + T(smooth quadratic Bézier curveto)
• C(smooth curveto) + S(curveto)

说明：T,S 是在 Q、C 的基础上，快速生成平滑曲线，且点的数量会减少一个

• Q+T 示例：M：起点，Q：两个点，T：一个点

<svg xmlns="http://www.w3.org/2000/svg" version="1.1" width="300" height="100">
    <desc>二次贝塞尔平滑曲线</desc><defs></defs>
    <path d="M20 10 Q140 40 180 20 T280 30" stroke="orange" stroke-width="3" fill="none"></path>
</svg>

• C+S 示例：M：起点，C：三个点，S：两个点

<svg xmlns="http://www.w3.org/2000/svg" version="1.1" width="300" height="100">
  <desc>三次贝塞尔平滑曲线</desc><defs></defs>
  <path d="M20 20 C90 40 130 40 180 20 S250 60 280 20" stroke="yellowgreen" stroke-width="3" fill="none"></path>
</svg>

webGl

容器是 canvas, 省略，感兴趣的可自行查阅

css + js

background-image: paint(worklet-name);

<!-- 1: 容器 -->
<div class="bg"></div>

<!-- 2: css -->
<style>
  .bg {
    background: paint(workletBezier); 
     100px;
    height: 100px;
  }
</style>

<!-- 3: -->
<script>
  if ('paintWorklet' in CSS) {
    // 必须是单独的js
    CSS.paintWorklet.addModule('workletBezier.js');
  }
</script>

<!-- workletBezier.js -->
<script>
class WorkletBezier {
  paint(context, canvas, properties) {
    context.beginPath();
    context.moveTo(20,20);
    context.bezierCurveTo(20,100,200,100,200,20);
    context.strokeStyle = 'dodgerblue';
    context.lineWidth = 3;
    context.stroke();
  }
}

registerPaint('workletBezier', WorkletBezier);
</script>

css, canvas, svg 三阶贝塞尔总结

• css 起点、终点固定，只需两个控制点
• canvas、svg, 一个M(moveto，起点)，加三个点（两控制点，一结束点）

高阶

高阶利用上面的公式，求出一个个点，再把点连接起来（需要考虑性能、精度问题）。

优化，可利用低价绘制高阶。

扩展

• 圆弧：canvas (arc，arcTo)、svg (path：A)
• 曲线上求控制点方法：二分法，牛顿迭代法，德卡斯特里奥算法
• h5 canvas n 阶贝塞尔曲线
• 物体跟随复杂曲线的轨迹运动

应用

1. 小球抛物线运动

        <style>
          .ball-wrap {
            position: relative;
          }
          .ball-outer {
            position: absolute;
            top: 30px;
            left: 27%;
            animation: parabola-x 1s linear infinite;
          }
          .ball {
             15px;
            height: 15px;
            background: orange;
            border-radius: 50%;
            box-shadow: 0 0 2px 0 #000;
            animation: parabola-y 1s cubic-bezier(.55,0,.85,.36) infinite;
          }
          @keyframes parabola-x {
            0% {
              transform: translateX(0);
            }
            100% {
              transform: translateX(200px);
            }
          }
          @keyframes parabola-y {
            0% {
              transform: translateY(15px);
            }
            100% {
              transform: translateY(200px);
            }
          }
        </style>
        <div class="ball-outer">
          <div class="ball"></div>
        </div>

2. 水波图

示例

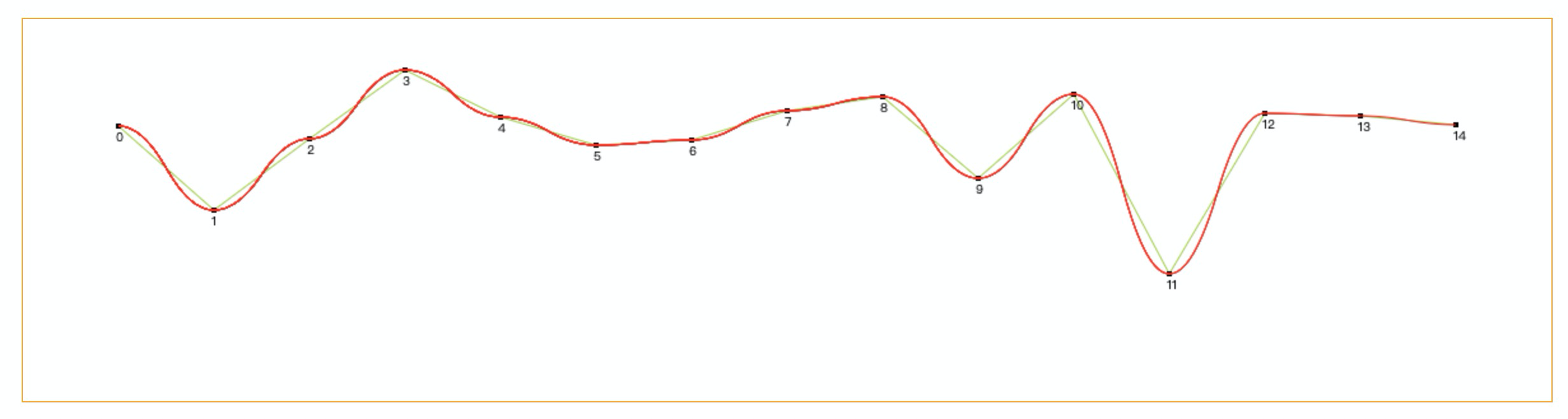
3. 如何根据已知的点数据绘制出一条平滑的曲线？

    let data = [
      { "date": "2020-04-24", "value": 84 },
      { "date": "2020-04-25", "value": 150 },
      { "date": "2020-04-26", "value": 94 },
      { "date": "2020-04-27", "value": 40 },
      { "date": "2020-04-28", "value": 77 },
      { "date": "2020-04-29", "value": 99 },
      { "date": "2020-04-30", "value": 95 },
      { "date": "2020-05-01", "value": 72 },
      { "date": "2020-05-02", "value": 61 },
      { "date": "2020-05-03", "value": 125 },
      { "date": "2020-05-04", "value": 59 },
      { "date": "2020-05-05", "value": 200 },
      { "date": "2020-05-06", "value": 74 },
      { "date": "2020-05-07", "value": 76 },
      { "date": "2020-05-08", "value": 83 }
    ]

    const canvas = document.querySelector('#canvas');
    const ctx = canvas.getContext('2d');

    const w = canvas.width;
    const h = canvas.height;

    let pos = [];
    function createPos() {
      data.forEach((item, i) => {
        pos.push({
          x: (i + 1) * (w / (data.length + 1)),
          y: item.value
        })
      })
    }
    createPos();

    // 折线
    function drawLine() {
      pos.forEach((item, i) => {
        if (i < pos.length - 1) {
          const start = item;
          const end = pos[i + 1];

          // 线段
          ctx.beginPath();
          ctx.moveTo(start.x, start.y);
          ctx.lineTo(end.x, end.y);
          ctx.lineWidth = 1;
          ctx.lineJoin = 'round';
          ctx.strokeStyle = 'yellowgreen';
          ctx.stroke();
        }

        // 点
        ctx.beginPath();
        ctx.fillRect(item.x - 2, item.y - 2, 4, 4);
        ctx.fillStyle = 'black';
        ctx.fill();
        ctx.closePath();

        // 文本
        ctx.fillText(i, item.x - 2, item.y + 12);
      })
    }
    drawLine();
 
   function getMiddlePos(a, b) {
      return (a + b) / 2;
    }     
 
   function drawCurve() {
      ctx.moveTo((pos[0].x), pos[0].y);

      pos.forEach((item, i) => {
        if (i < pos.length - 1) {
          const a = pos[i];
          const b = pos[i + 1];
          const m = {
            x: getMiddlePos(a.x, b.x),
            y: getMiddlePos(a.y, b.y)
          }
          const ammx = getMiddlePos(a.x, m.x);
          const mbmx = getMiddlePos(m.x, b.x);

          ctx.quadraticCurveTo(ammx, a.y, m.x, m.y);
          ctx.quadraticCurveTo(mbmx, b.y, b.x, b.y);

          ctx.lineWidth = 1;
          ctx.strokeStyle = 'red';
          ctx.stroke();
        }
      })
    }
    drawCurve();

效果图：