转自：http://lanqi.org/skills/10939/
卡特兰数 — 计数的映射方法的伟大胜利
卡特兰（Catalan）数来源于卡特兰解决凸$n+2$边形的剖分时得到的数列$C_n$，在数学竞赛、信息学竞赛、组合数学、计算机编程等方面都会有其不同侧面的介绍．卡特兰问题的解决过程应用了大量的映射方法，堪称计数的映射方法的典范．为了便于读者理解，我们先介绍一些卡特兰问题的简单变形，再介绍卡特兰问题及其解法．
问题一 进出栈
栈是一种先进后出（FILO，First In Last Out）的数据结构．如图1，$1,2,3,4$顺序进栈，那么一种可能的进出栈顺序是$$1 In o 2 In o 2 Out o 3 In o 4 In o 4 Out o 3 Out o 1 Out,$$于是出栈序列为$1,3,4,2$．
图1 栈是先进后出的数据结构
那么一个足够大的栈的进栈序列为$1,2,3,cdots,n$时有多少个不同的出栈序列？
解 首先，每一种进出栈的顺序都与出栈序列一一对应．也就是说，如果我们用$+1$表示进栈，$-1$表示出栈，那么题中示例中的出栈序列$1,3,4,2$与进出栈顺序$$+1,+1,-1,+1,+1,-1,-1,-1,$$是对应的．
那么对$n$个数的序列，总的进出栈顺序是给$2n$个$1$前面挑$n$个添加$+$号，其他的添加$-$号，共${ m C}_{2n}^n$种吗？
答案是否定的，这是因为出栈的前提是有进栈动作，于是要求每个排列中的前若干项和均不为负数，也就是说排列$$1,-1,-1,1,1,-1,-1,1$$是无效的．
那么无效的排列到底有多少呢？
考虑$M$是所有无效的排列构成的集合，考虑其中第一次发现排列无效的时候，也就是第一次发现其前若干项和为$-1$的时候，此时我们将包含使得前若干项和为$-1$的这一项开始的之前的所有项全都取相反数，那么就会得到一个新的排列，这个排列包含$n+1$个$+1$，以及$n-1$个$-1$，设所有这样的排列构成集合$N$．
显然，这个$M o N$的映射是一一映射（$N$中的每一个排列从第一项往后累积求和的时候必然会出现和为$+1$的情形，此时将排列中使得和为$+1$的这一项连同之前的所有项全部取相反数，那么就会得到$M$中的一个排列）．
因此无效的排列共有${ m C}_{2n}^{n-1}$个．
综上，所有不同的出栈序列总数为${ m C}_{2n}^n-{ m C}_{2n}^{n-1}$，即$dfrac 1{n+1}{ m C}_{2n}^n$．
进出栈问题的一个简单变形就是二叉树问题：
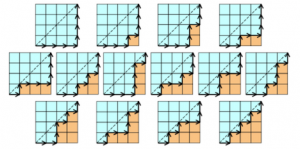
求$n+1$个叶子的满二叉树的个数，如图8．
图8 n+1个叶子的满二叉树的个数问题
事实上，向左记为$+1$，向右记为$-1$，按照向左优先的原则，从根节点开始遍历．例如第一个图记为$$+1,+1,+1,-1,-1,-1,$$于是由卡特兰数的含义可得满二叉树的个数为$C_n$．
问题二 电影购票
电影票每张$50$元，如果有$m + n$个人排队买票，其中$m$个人各持有$50$元面值的钞票$1$张，另外$n$个人各持有$100$元面值的钞票$1$张，而票房没有预备找零．有多少种方法可以将这$m+n$个人排成一列，顺序购票，使得无需因为等待找零而耽误时间？
解 我们给进出栈问题一个几何模型：
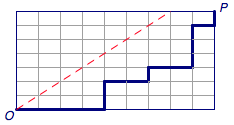
如图2，在$n imes n$的方格地图中，从一个角到另一个角（成对角线），不跨越对角线的路径数．
图2 方格地图中的受限路径数
只要将向右记为$+1$，向上记为$-1$，就转化成了问题一．
利用这个模型，我们解决这个卡特兰问题的变形问题，并顺便给进出栈问题的解法一个几何解释．
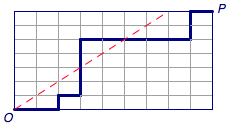
如图3，在一个$m imes n$的网格中，从左下角的原点$Oleft( {0,0} ight)$出发，每次向右（表示接待的观众持有$50$元的钞票）或向上（表示接待的观众持有$100$元的钞票）移动，最终到达$Pleft( {m,n} ight)$．我们需要找到在直线$y = x$下方（包括边界）的路径条数．
图3 矩形地图中的受限路径数
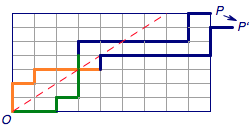
从反面考虑问题．设$M$为穿过直线$y = x$（表示会经过直线上方的点）的从$O o P$的路径组成的集合，如图4．
图4 犯规的路径
如图5，利用对称可以将$M$中第一次犯规时的路径对称，然后再将剩下的部分接在对称后的路径上，由于此时将一次向上移动修改为了向右移动，因此终点由$P$变成了$P'$，此时就建立了与$O$到$P'$的路径的一个一一映射．
图5 利用对称建立对应关系
因此$${ m{card}}(M)= { m{card}}(N)={ m{C}}_{m + n}^{n-1},$$于是所求的排列数为$${ m{C}}_{m + n}^n-{ m{C}}_{m + n}^{n-1}.$$特别的，当$m = n$时有$${ m{C}}_{m + n}^n-{ m{C}}_{m + n}^{n-1} = { m{C}}_{2n}^n-{ m{C}}_{2n}^{n-1} = dfrac{1}{{n + 1}}{ m{C}}_{2n}^n,$$即卡特兰数．
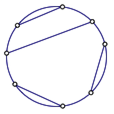
问题三 圆内连弦
如图6，圆周上有$2n$个点，以这些点为端点连互不相交的$n$条弦，求不同的连法总数．
图6 圆内连弦问题
解 为了解决这个问题，我们重新解释卡特兰数的推导方式．先解决下面的辅助问题：
圆周上有$2n + 1$个点，其中$n + 1$个点上标“$ + 1$”，$n$个点上标“$ - 1$”，如果可以找到某个标有“$ + 1$”的点作为起点，当顺时针沿圆周前进时将所遇到的点（包括起点）上标的数相加得到的和始终为正数，就称这种标记法是好标记法．求好标记法的总数（注意考虑圆排列）．
辅助问题的解 对于任何一种标记法，我们将顺时针相邻的“$ + 1$”“$ - 1$”（指顺时针前进时先遇到“$ + 1$”后遇到“$ - 1$”）同时抹去，可以证明抹去的前后对标记法的好坏没有影响．不停的重复这一过程，则最后只剩一个标有“$ + 1$”的点，显然此时标记法为好的．因此所有的标记法都是好标记法，显然其数目为$$dfrac{1}{{2n + 1}}{ m{C}}_{2n + 1}^n = dfrac{1}{{n + 1}}{ m{C}}_{2n}^n.$$
问题的解 通过对辅助问题的进一步探索可知，每一种将圆周上$2n + 1$个点标记为$n + 1$个$ + 1$点，和$n$个$ - 1$点的方法唯一确定一个顺时针前进的方案（即起点）．我们将这个起点删去，剩下的$2n$个点在顺时针方向上一定为“$ + 1$”“$ - 1$”“$ + 1$”“$ - 1$”，…，此时将顺时针相邻的这些“$ + 1$”“$ - 1$”点用弦连接起来，就得到互不相交的$n$条弦．这样我们就建立了从好标记法到弦的连法的单射．
反过来，如果我们有了一种弦的连法，就可以从某条弦的端点出发顺时针前进，对每条弦的两个端点都是先遇到的端点标上“$ + 1$”，后遇到的端点标上“$ - 1$”，然后在最后回到出发点时添上一个标有“$ + 1$”的点．这样我们就建立了从弦的连法到好标记法的单射．
综上，所求的不同连法数为$dfrac{1}{{n + 1}}{ m{C}}_{2n}^n$．
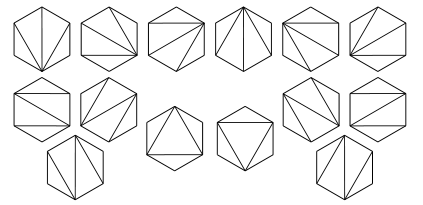
问题四 凸多边形的剖分（卡特兰问题）
求凸$n+2$边形用其$n-1$条对角线分割为互不重叠的三角形的分法总数．
图7 凸n+2边形的所有剖分方法总数
解 先介绍两个关于卡特兰数$C_n$的小引理，将问题一中的$+1$和$-1$分别看成左括号和右括号，我们得到
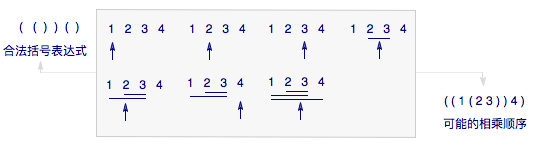
引理一 由$n$对括号形成的合法括号表达式的个数为$C_n$．
比如$n=3$时，所有合法的括号表达式有$$((())),(())(),()(()),()()(),(()()),$$共$5$个．
考虑$n+1$个数相乘，不同的相乘顺序的数目．我们可以给出每一个合法的括号表达式和一种可能的相乘顺序的对应方式．如$n=3$时，先取$4$个数$a,b,c,d$，然后在第一个数下设一个指针，将一个左括号看成是指针右移一格，而将右括号看成是将指针当前指向的数与其左侧的一个数作乘积，并删除左侧的那个数，那么当执行完括号表达式，就得到了一种可能的相乘顺序，如图8．
图8 合法括号表达式与可能的相乘顺序的对应
这样我们就从引理一出发得到了
引理二 $n+1$个数连乘，不同的乘法顺序数为$C_n$．
注 这样也是RPN模式的计算机的工作模式，可以无需括号完成计算，从而节省按键的次数．这种计算器在财务计算中大量使用，如图．
图9 Mac OS X下计算器的PRN模式
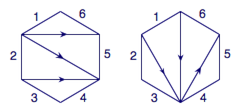
接下来解决卡特兰问题，用$1,2,3,cdots ,n+2$标记凸$n+2$边形的边，从标记为$1$的边的起点（按逆时针方向）开始按未标记的对角线均为向外标记方向，如图10．
图10 分别标记边和对角线
进而，逆时针读图，将出的箭头读为左括号，进的箭头读为右括号，就得到了剖分方式与连乘顺序的对应．图10中的两个图对应的连乘顺序表达式分别为$$1((2(34))5)6,(1(23))(45)6,$$抛开$6$不计，每个连乘顺序表达式实际上就是规定了$n+1$个数连乘时，不同的乘法顺序，根据引理一，得到剖分方式的总数为$C_n$．
卡特兰数的性质
卡特兰数有一些优美的性质，如
通项公式一 $C_n=dfrac{1}{n+1}{ m C}_{2n}^n={ m C}_{2n}^n-{ m C}_{2n}^{n-1}$；
通项公式二 $C_n=dfrac{1}{n+1}sumlimits_{i=0}^nleft({ m C}_n^i ight)^2$；
递推公式一 $C_{n+1}=dfrac{2(2n+1)}{n+2}C_n$，且$C_0=1$；
递推公式二 $C_{n+1}=sumlimits_{i=0}^nC_iC_{n-i}$，且$C_0=1$；
增长速度 $Delta C_nsimdfrac{4^n}{n^{frac 32}sqrt{pi}}$．
由卡特兰问题以及其各种变形很容易推导卡特兰数的递推公式．相应的，我们也可以利用递推公式二来发现和证明某些卡特兰问题的变形，比如：
探索用$n$个长方形去填充一个高度为$n$的阶梯图形的方法数，如图11．
图11 阶梯图形的填充
解 把包含左上角的矩形去掉，就很容易由递推公式二推得所有填充方法数就是卡特兰数$C_n$了．