先来了解几个概念:排列数,组合数。
一、定义及有用的性质
排列数:从n个不同元素中依次取出m个元素排成一列的方案数。P(n,m)=n!/(n-m)!
组合数:从n个不同元素中依次取出m个元素形成一个集合的方案数。(注意,集合满足无序性,这是和排列数的区别)。C(n,m)=n!/m!(n-m)!
组合数性质
性质1 C(n,m)= C(n,n-m)
性质2 C(n,m)=C(n-1,m-1)+C(n-1,m)
性质3 C(n,0)+C(n,1)+C(n,2)+...+C(n,n)=2^n(道出组合数与杨辉三角间的联、系)
二、组合数球阀
① 递推 复杂度为n²
c[i][j]=c[i-1][j]+c[i-1][j-1]
但是要注意要命的初始化--
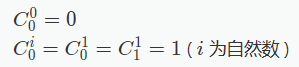
丢一段代码跑。

② 预处理阶乘+逆元 复杂度为nlogn
首先我们应该知道,除以一个数等于乘上这个数的逆元,那么我们就可以直接(生猛 地利用原始带有阶乘的公式,分母我们处理逆元。这里用到的是最简单的费马小定理方法,一个数x在膜p意义下的逆元等于x^(p-2)
丢一段代码跑。这个方法的使用条件是p为素数!

1 #include<cstdio> 2 #include<algorithm> 3 4 using namespace std; 5 typedef long long ll; 6 const int p=1e9+7; 7 8 ll n,k,x; 9 ll ans=1; 10 11 ll ksm(ll a,ll b) 12 { 13 ll tmp=1; 14 while(b) 15 { 16 if(b&1) tmp=tmp*a%p; 17 b>>=1; 18 a=a*a%p; 19 } 20 return tmp; 21 } 22 23 int main() 24 { 25 //求C(n,k) 26 scanf("%d%d",&n,&k); 27 for(int i=1;i<=n;i++) ans=ans*i%p; 28 for(int i=1;i<=k;i++) ans=ans*ksm(i,p-2)%p; 29 for(int i=1;i<=n-k;i++) ans=ans*ksm(i,p-2)%p; 30 printf("%lld",ans); 31 return 0; 32 }
*Update 费马小定理有的时候可能会复杂度爆炸 这里介绍一种exgcd求逆元的方法

1 ll exgcd(ll a,ll b,ll &x,ll &y) 2 { 3 if(b==0) 4 { 5 x=1; 6 y=0; 7 return a; 8 } 9 int gu=exgcd(b,a%b,x,y); 10 int t=x; 11 x=y; 12 y=t-a/b*y; 13 return gu; 14 15 } 16 17 ll niyuan(ll hu) 18 { 19 x=0,y=0; 20 ll tmp=exgcd(hu,p,x,y); 21 return (x+p)%p; 22 } 23 24 ll C(ll k,ll m) 25 { 26 ll up=fac[k]%p; 27 ll down=fac[m]%p*fac[k-m]%p; 28 ll ans=up*niyuan(down)%p; 29 return ans; 30 }
③ 分解质因数 复杂度为nlogn
前导芝士:算术分解定理。
我们把分子分母都进行分解质因数,把整个分子分母对应的质因数的指数相减(消去)
丢一段代码跑。

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 typedef long long LL; 5 int n,m; 6 int p; 7 int i,j; 8 int tot; 9 int prim[100010],cnt[100010]; 10 bool flag[100010]; 11 12 void fj(int a,int k)//分解质因数 k=1/-1 13 {//k==1时为分子操作 质因子数++ 14 //k==-1时为分母操作 质因子数-- 15 int x=a; 16 for (int i=1;i<=tot;i++) 17 { 18 if (x%prim[i]==0) 19 { 20 while (x%prim[i]==0) x/=prim[i],cnt[prim[i]]+=k; 21 } 22 if (x==1) break; 23 if (prim[i]*prim[i]>n) break; 24 } 25 if (x>1) cnt[x]+=k; 26 } 27 28 int Pow(int x,int a) 29 { 30 int ans=1; int j=1; 31 while (j<=a) 32 { 33 if (j&a) ans=((LL)ans*(LL)x)%p; 34 j<<=1; 35 x=((LL)x*(LL)x)%p; 36 } 37 return ans; 38 } 39 40 int main() 41 { 42 scanf("%d%d%d",&n,&m,&p); 43 //筛素数 44 for (i=2; i<=n; i++) 45 { 46 if (!flag[i]) prim[++tot]=i; 47 for (j=1; j<=tot; j++) 48 { 49 if (prim[j]*i>n) break; 50 flag[prim[j]*i]=1; 51 if (i%prim[j]==0) break; 52 } 53 } 54 //printf("/////"); 55 int a=m; int b=(n-m); 56 int c=max(a,b); 57 //一定有一部分会自己消去(上下完全相同) 58 for (i=c+1; i<=n; i++) 59 {//分子操作 60 fj(i,1); 61 } 62 //分母操作 63 for (i=1;i<=min(a,b);i++) fj(i,-1); 64 int ans=1; 65 for (i=1; i<=n; i++) 66 { 67 if (cnt[i]>0) ans=((LL)ans*Pow(i,cnt[i]))%p; 68 } 69 printf("%d ",ans); 70 return 0; 71 }
