前缀和小结 By cellur925

这篇主要是来介绍前缀和的QAQ。

前缀和有一维的和二维的，一维的很容易理解，高中数学必修5第二章数列给出了前n项和的概念，就是前缀和。一维的我们在这里简单说一句。

一维前缀和

预处理：在输入一个数列的时候累加

查询区间和：查询[i,j]区间全部元素的和--sum[j]-sum[i-1]

二维前缀和

预处理：用到了容斥原理的知识。即求矩阵左上角的顶点与当前点所围成的矩形所覆盖的权值。

              设f[][]为前缀和数组，则f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+a[i][j]

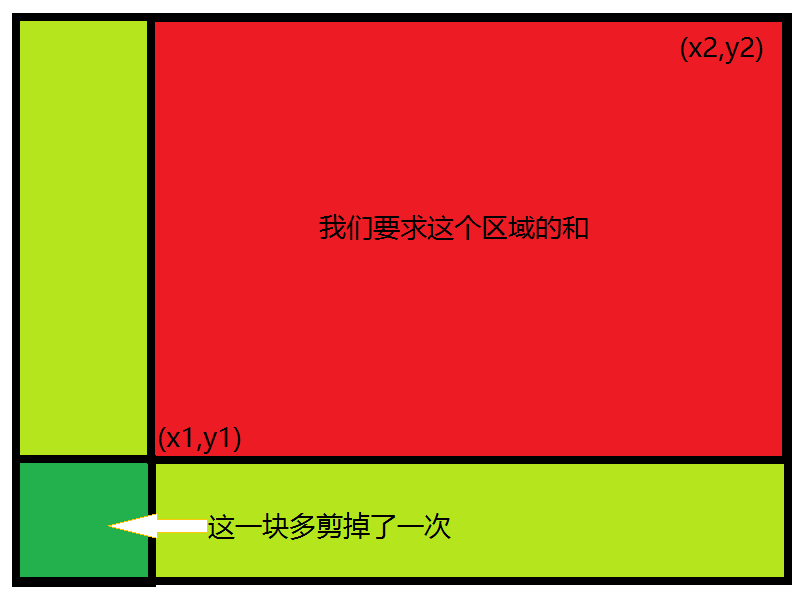
（注：图片来源@ShawnZhou 神犇，原文地址，感谢，侵删。）

查询区间和：

　　对于一个边长为R的正方形，以(i,j)作为右下角的，那它矩阵中的和为

　　s[i][j]-s[i-R,j]-s[i,j-R]+s[i-R,j-R]

放两道例题跑（

例题1 [HNOI2003]激光炸弹

前缀和+枚举边长

#include<cstdio>
#include<algorithm>
using namespace std;
int n,R,ans;
int f[5090][5090];
int main()
{
    scanf("%d%d",&n,&R);
    for(int i=1;i<=n;i++)
    {
        int x=0,y=0,z=0;
        scanf("%d%d%d",&x,&y,&z);
        f[x+1][y+1]=z;
    } 
    for(int i=1;i<=5001;i++)
     for(int j=1;j<=5001;j++)
     {
         f[i][j]+=f[i-1][j]+f[i][j-1]-f[i-1][j-1];
     }
    for(int i=0;i<=5000-R;i++)
     for(int j=0;j<=5000-R;j++)
     {
         int tmp=f[i+R][j+R]-f[i+R][j]-f[i][j+R]+f[i][j];
         ans=max(tmp,ans);
     }
    printf("%d",ans);
    return 0;
} 

例题2 最大正方形

可能是隐藏在dp标签下的一个叛徒这题我觉得用前缀和最简单，而且还是01矩阵，只要预处理出前缀和然后枚举最大正方形的边长大小，再看矩阵中权值和是否等于边长*边长即可。以及注意边界问题。

#include<cstdio>
#include<algorithm>

using namespace std;

int n,m,ans;
int f[200][200];

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&f[i][j]);
            f[i][j]+=f[i-1][j]+f[i][j-1]-f[i-1][j-1];
        }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            for(int k=1;k<=max(n,m);k++)
            {
                if(i-k<1) continue;
                if(j-k<1) continue;
                int qwq=f[i][j]-f[i-k][j]-f[i][j-k]+f[i-k][j-k];
                if(qwq==k*k) ans=max(ans,k);
            }
    printf("%d",ans);
    return 0;
}

---

*update on 10-18

noip2014无线网络发射器选址

二维前缀和裸题，当然也可直接枚举中心统计。

但是发现自己前缀和这理解可能有点问题hhh。

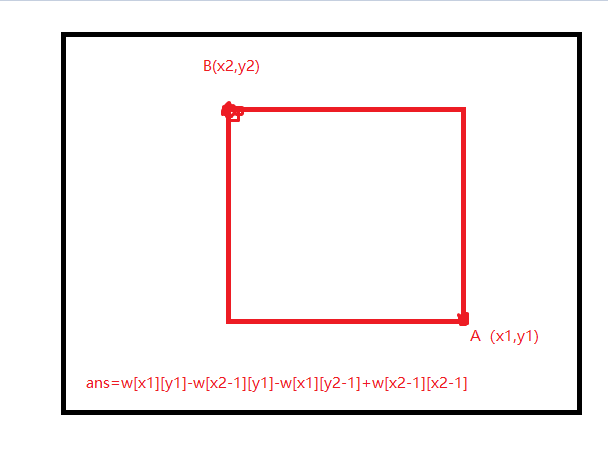
其实是这样的qwq。（当然变量名不能用x1y1之类的啦）

#include<cstdio>
#include<algorithm>
#include<iostream> 

using namespace std;
typedef long long ll;

int d,n;
ll tot,ans;
ll w[500][500];

int main()
{
//    freopen("1.out","w",stdout);
    scanf("%d%d",&d,&n);
    for(int i=1;i<=n;i++)
    {
        int x=0,y=0,z=0;
        scanf("%d%d%d",&x,&y,&z);
        w[x][y]=z;
    }
    for(int i=0;i<=128;i++)
        for(int j=0;j<=128;j++)
            w[i][j]+=w[i-1][j]+w[i][j-1]-w[i-1][j-1];
    for(int i=0;i<=128;i++)
        for(int j=0;j<=128;j++)
        {
            //if(i-d<0||i+d>128||j-d<0||j+d>128) continue;
            int tx=(i+d<=128) ? (i+d) : 128;
            int ty=(j+d<=128) ? (j+d) : 128;
            int lx=(i-d>=0) ? (i-d) : 0;
            int ly=(j-d>=0) ? (j-d) : 0;
            ll tmp=w[tx][ty]-w[tx][ly-1]-w[lx-1][ty]+w[lx-1][ly-1];
            //if(i==120&&j==120) cout<<tx<<" "<<ty<<" "<<lx<<" "<<ly;
            //if(i==120&&j==120) cout<<tmp;
            if(tmp>ans) ans=tmp,tot=1;
            else if(tmp==ans) tot++;
        }
    printf("%lld %lld",tot,ans);
    return 0;
}