题目链接:http://codeforces.com/contest/976
String can be called correct if it consists of characters "0" and "1" and there are no redundant leading zeroes. Here are some examples: "0", "10", "1001".
You are given a correct string s.
You can perform two different operations on this string:
- swap any pair of adjacent characters (for example, "101"
 "110");
"110"); - replace "11" with "1" (for example, "110"
 "10").
"10").
Let val(s) be such a number that s is its binary representation.
Correct string a is less than some other correct string b iff val(a) < val(b).
Your task is to find the minimum correct string that you can obtain from the given one using the operations described above. You can use these operations any number of times in any order (or even use no operations at all).
The first line contains integer number n (1 ≤ n ≤ 100) — the length of string s.
The second line contains the string s consisting of characters "0" and "1". It is guaranteed that the string s is correct.
Print one string — the minimum correct string that you can obtain from the given one.
4
1001
100
1
1
1
In the first example you can obtain the answer by the following sequence of operations: "1001"  "1010"
"1010"  "1100"
"1100"  "100".
"100".
In the second example you can't obtain smaller answer no matter what operations you use.
题意:对于一串由01构成的字符串有两种操作,一种是将01->10,一种是11->1。将该字符串进行这两种操作后,问生成的最小数是多少。
思路:就是记录0和1的个数,如果有1,那么就输出一个1,剩下有多少个0就补在1后面;没有1就输出0即可。
代码实现如下:
1 #include <iostream> 2 #include <string> 3 using namespace std; 4 5 int n, ans1, ans2; 6 string s; 7 8 int main() { 9 cin >> n; 10 cin >> s; 11 if(n == 1) { 12 cout << s << endl; 13 return 0; 14 } 15 ans1 = 0, ans2 = 0; 16 for(int i = 0; i < n; i++) { 17 if(s[i] == '0') { 18 ans1++; 19 } else { 20 ans2++; 21 } 22 } 23 cout <<'1'; 24 for(int i = 0; i < ans1; i++) { 25 cout <<'0'; 26 } 27 cout <<endl; 28 return 0; 29 }
You might have heard about the next game in Lara Croft series coming out this year. You also might have watched its trailer. Though you definitely missed the main idea about its plot, so let me lift the veil of secrecy.
Lara is going to explore yet another dangerous dungeon. Game designers decided to use good old 2D environment. The dungeon can be represented as a rectangle matrix of n rows and m columns. Cell (x, y) is the cell in the x-th row in the y-th column. Lara can move between the neighbouring by side cells in all four directions.
Moreover, she has even chosen the path for herself to avoid all the traps. She enters the dungeon in cell (1, 1), that is top left corner of the matrix. Then she goes down all the way to cell (n, 1) — the bottom left corner. Then she starts moving in the snake fashion — all the way to the right, one cell up, then to the left to the cell in 2-nd column, one cell up. She moves until she runs out of non-visited cells. n and m given are such that she always end up in cell (1, 2).
Lara has already moved to a neighbouring cell k times. Can you determine her current position?
The only line contains three integers n, m and k (2 ≤ n, m ≤ 109, n is always even, 0 ≤ k < n·m). Note that k doesn't fit into 32-bit integer type!
Print the cell (the row and the column where the cell is situated) where Lara ends up after she moves k times.
4 3 0
1 1
4 3 11
1 2
4 3 7
3 2
Here is her path on matrix 4 by 3:
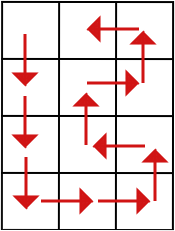
题意:给你一个n*m的棋盘,进行蛇形走位(如图),问第k次位移后的坐标。
思路:找规律~(注意k会爆int)
代码实现如下:
1 #include <cstdio> 2 3 long long n, m, k; 4 5 int main() { 6 while(~scanf("%I64d%I64d%I64d", &n, &m, &k)) { 7 k = k + 1; 8 if(k <= n) { 9 printf("%I64d 1 ", k); 10 continue; 11 } 12 k = k - n; 13 int t = (k - 1) / (m - 1), x = k - (m - 1) * t; 14 if(t % 2) { 15 printf("%I64d %I64d ", n - t, m - x + 1); 16 } else { 17 printf("%I64d %d ", n - t, x + 1); 18 } 19 } 20 }
You are given a sequence a1, a2, ..., an of one-dimensional segments numbered 1 through n. Your task is to find two distinct indices i and j such that segment ai lies within segment aj.
Segment [l1, r1] lies within segment [l2, r2] iff l1 ≥ l2 and r1 ≤ r2.
Print indices i and j. If there are multiple answers, print any of them. If no answer exists, print -1 -1.
The first line contains one integer n (1 ≤ n ≤ 3·105) — the number of segments.
Each of the next n lines contains two integers li and ri (1 ≤ li ≤ ri ≤ 109) — the i-th segment.
Print two distinct indices i and j such that segment ai lies within segment aj. If there are multiple answers, print any of them. If no answer exists, print -1 -1.
5
1 10
2 9
3 9
2 3
2 9
2 1
3
1 5
2 6
6 20
-1 -1
In the first example the following pairs are considered correct:
- (2, 1), (3, 1), (4, 1), (5, 1) — not even touching borders;
- (3, 2), (4, 2), (3, 5), (4, 5) — touch one border;
- (5, 2), (2, 5) — match exactly.
题意:给你n个区间,找到两个区间使得一个包含另一个,输出对应的序号,不存在就输出-1 -1
代码实现如下:
1 #include <cstdio> 2 #include <algorithm> 3 using namespace std; 4 5 const int maxn = 3e5 + 7; 6 7 int n; 8 int R[maxn]; 9 10 struct node { 11 int l, r, id; 12 bool operator < (const node& p) const { 13 return l == p.l ? r > p.r : l < p.l; 14 } 15 }line[maxn]; 16 17 int main() { 18 while(~scanf("%d", &n)) { 19 for(int i = 0; i < n; i++) { 20 scanf("%d%d", &line[i].l, &line[i].r); 21 line[i].id = i + 1; 22 } 23 sort(line, line+n); 24 for(int i = 0; i < n; i++) { 25 R[i] = line[i].r; 26 } 27 int flag = 0; 28 for(int i = 1; i < n; i++) { 29 int pos = lower_bound(R, R + i, line[i].r) - R; 30 if(pos != i) { 31 printf("%d %d ", line[i].id, line[pos].id); 32 flag = 1; 33 break; 34 } 35 } 36 if(!flag) printf("-1 -1 "); 37 } 38 return 0; 39 }
Recently Max has got himself into popular CCG "BrainStone". As "BrainStone" is a pretty intellectual game, Max has to solve numerous hard problems during the gameplay. Here is one of them:
Max owns n creatures, i-th of them can be described with two numbers — its health hpi and its damage dmgi. Max also has two types of spells in stock:
- Doubles health of the creature (hpi := hpi·2);
- Assigns value of health of the creature to its damage (dmgi := hpi).
Spell of first type can be used no more than a times in total, of the second type — no more than b times in total. Spell can be used on a certain creature multiple times. Spells can be used in arbitrary order. It isn't necessary to use all the spells.
Max is really busy preparing for his final exams, so he asks you to determine what is the maximal total damage of all creatures he can achieve if he uses spells in most optimal way.
The first line contains three integers n, a, b (1 ≤ n ≤ 2·105, 0 ≤ a ≤ 20, 0 ≤ b ≤ 2·105) — the number of creatures, spells of the first type and spells of the second type, respectively.
The i-th of the next n lines contain two number hpi and dmgi (1 ≤ hpi, dmgi ≤ 109) — description of the i-th creature.
Print single integer — maximum total damage creatures can deal.
2 1 1
10 15
6 1
27
3 0 3
10 8
7 11
5 2
26
In the first example Max should use the spell of the first type on the second creature, then the spell of the second type on the same creature. Then total damage will be equal to 15 + 6·2 = 27.
In the second example Max should use the spell of the second type on the first creature, then the spell of the second type on the third creature. Total damage will be equal to 10 + 11 + 5 = 26.
题意:Max有n只生物,生物有hp和dmg(破坏力)两种属性,你有两种操作,一种是将hp = 2 * hp,一种是dmg = hp,这两种操作的数量为a,b,问怎样才能使所有的生物的总dmg最大~
思路:先将所有的生物按照hp-dmg从大到小进行排序,然后轮流进行hp=hp*2的操作(坑点:b=0)。
代码实现如下:
1 #include <cstdio> 2 #include <iostream> 3 #include <algorithm> 4 using namespace std; 5 6 typedef long long ll; 7 const int maxn = 2e5 + 7; 8 int n, a, b; 9 ll ans; 10 11 struct node { 12 ll hp, dmg, dif; 13 bool operator < (const node& p) const { 14 return dif > p.dif; 15 } 16 } creatures[maxn]; 17 18 int main() { 19 cin >> n >> a >> b; 20 ans = 0; 21 for (int i = 0; i < n; i++) { 22 cin >> creatures[i].hp >> creatures[i].dmg; 23 creatures[i].dif = max(creatures[i].hp - creatures[i].dmg, 0LL); 24 ans += creatures[i].dmg; 25 } 26 if (b == 0) { 27 cout << ans << endl; 28 return 0; 29 } 30 sort(creatures, creatures + n); 31 ll tot = 0, sum = 0; 32 for (int i = 0; i < min(b, n); i++) { 33 tot += creatures[i].dif; 34 } 35 int pw = 1 << a; 36 sum = tot; 37 for (int i = 0; i < min(b, n); i++) { 38 sum = max(sum, tot - creatures[i].dif + (creatures[i].hp * pw) - creatures[i].dmg); 39 } 40 for (int i = b; i < n; i++) { 41 sum = max(sum, tot - creatures[b - 1].dif + (creatures[i].hp * pw) - creatures[i].dmg); 42 } 43 cout << sum + ans << endl; 44 return 0; 45 }