数据平滑
是用来处理噪声数据,使数据变化较为平顺.可以使用移动平均线, 也可以使用hanning函数
Key_Function
np.hanning函数: 是一个加权余弦的窗函数, 相当于是余弦移动平均线
np.polysub函数: 输入两个多项式系数数组, 返回一个表示两个多项式差的多项式的系数数组
np.isreal函数: 判断数组元素是否是实数
np.select函数: 根据给定的条件, 从数组中挑选出符合条件的元素并组成数组返回
np.trim_zeros函数: 去掉一维数组中开头或末尾为0的元素
Code
import numpy as np import matplotlib.pyplot as plt N = 8 weights = np.hanning(N) print(weights) ''' [ 0. 0.1882551 0.61126047 0.95048443 0.95048443 0.61126047 0.1882551 0. ] ''' # 本例使用的是收盘价 bhp = np.loadtxt('BHP.csv', delimiter=',', usecols=(6,), unpack=True) bhp_returns = np.diff(bhp) / bhp[:-1] print(len(bhp_returns)) # 29 smooth_bhp = np.convolve(weights/weights.sum(), bhp_returns)[N-1:-N+1] # 使用归一化的weights作为权重 vale = np.loadtxt('VALE.csv', delimiter=',', usecols=(6,), unpack=True) vale_returns = np.diff(vale) / vale[:-1] smooth_vale = np.convolve(weights/weights.sum(), vale_returns)[N-1:-N+1] t = np.arange(N-1, len(bhp_returns)) plt.plot(t, bhp_returns[N-1:], lw=1.0) plt.plot(t, smooth_bhp, lw=3.0) plt.plot(t, vale_returns[N-1:], lw=5.0) plt.plot(t, smooth_vale, lw=7.0) plt.show()
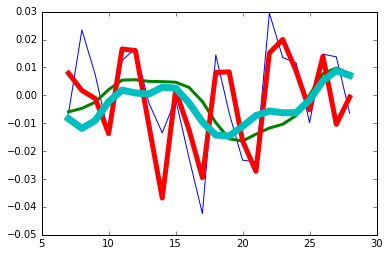
接上面代码
# 使用多项式拟合平滑后的数据 K = 8 t = np.arange(N-1, len(bhp_returns)) poly_bhp = np.polyfit(t, smooth_bhp, K) poly_vale = np.polyfit(t, smooth_vale, K) # 求解两条曲线的交叉点 # 通过求两个多项式的差, 然后对所得的多项式求根 poly_sub = np.polysub(poly_bhp, poly_vale) xpoints = np.roots(poly_sub) ''' [ 27.73321597+0.j 27.51284094+0.j 24.32064343+0.j 18.86423973+0.j 12.43797190+1.73218179j 12.43797190-1.73218179j 6.34613053+0.62519463j 6.34613053-0.62519463j] ''' reals = np.isreal(xpoints) print(reals) # [ True True True True False False False False] xpoints = np.select([reals], [xpoints]) print(xpoints) ''' [ 27.73321597+0.j 27.51284094+0.j 24.32064343+0.j 18.86423973+0.j 0.00000000+0.j 0.00000000+0.j 0.00000000+0.j 0.00000000+0.j] ''' xpoints = xpoints.real print(xpoints) ''' [ 27.73321597 27.51284094 24.32064343 18.86423973 0. 0. 0. 0. ] ''' print(np.trim_zeros(xpoints)) # [ 27.73321597 27.51284094 24.32064343 18.86423973]