寻找无序数组中第K大的数
一、代码
// 寻找无序数组 nums 的 [from, end] 范围中第 K 大的数。K 为 0 基,即 K = 0 代表找第 1 大的数。
// 默认参数均合法
private void findKthLargest(int[] nums, int from, int end, int k) {
// 随机取数组中的一个元素为标准,使查找时间更稳定
int randomIdx = from + (int) (Math.random() * (end - from));
swap(nums, randomIdx, end);
// ============= 核心逻辑 ===============
int left = from - 1, right = left;
for (int i = from; i <= end; i++) {
if (nums[i] > nums[end]) {
swap(nums, ++right, i);
swap(nums, ++left, right);
} else if (nums[i] == nums[end]) {
swap(nums, ++right, i);
}
}
// ======================================
// 注意 if 和 递归 的边界条件
if (from + k > left && from + k <= right) {
return;
} else if (from + k > right) {
findKthLargest(nums, right + 1, end, from + k - right - 1);
} else {
findKthLargest(nums, from, left, k);
}
}
private static void swap(int[] arr, int index1, int index2) {
int tepm;
tepm = arr[index1];
arr[index1] = arr[index2];
arr[index2] = tepm;
}
二、解析
思想类似于快排,每次取数组中的一个数 x,然后将比 x 大的数全部放到其左边,此时 x 在数组中的位置即确定,若 x 的位置刚好为所求 k,则结束。
具体代码实现为:
1、选择一个基准 x,将其置换到数组末;
2、使用 left、right 双指针,初始时均指向 left - 1 处,然后 i 在 [from, end] 中循环,a. 当 arr[i] 等于x时,right 后移一位,再置换 i 和 right 指向的元素。 b. 当 arr[i] 大于x时,right 后移一位,再置换 i 和 right 指向的元素,然后 left 后移一位,再置换 left 和 right 指向的元素。这样使得,left <= right <= i 并且 left(含)之前的都比 x 大,right(不含)之后的都比 x 小。于是,循环结束后 [from, left] 的数皆大于 x,(right, end] 皆小于 x,(left, right] 皆等于 x,这样(left,right] 在数组中的顺序就都确定了。
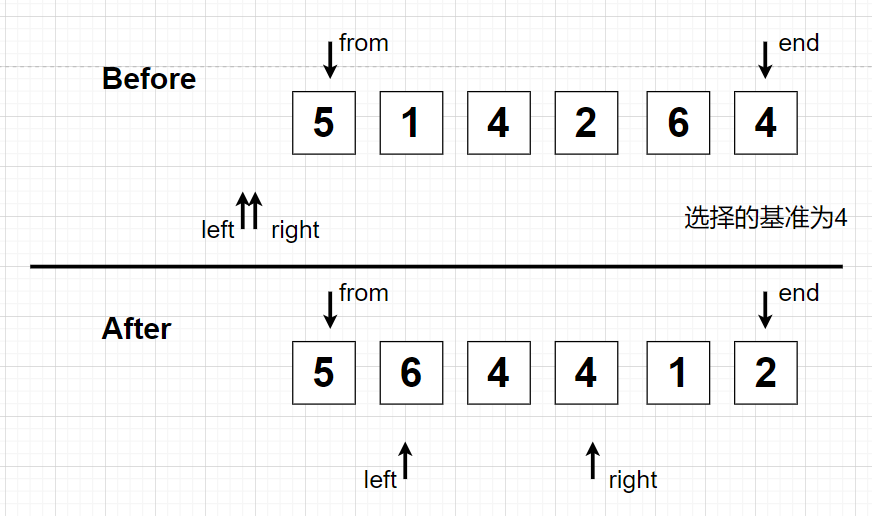
3、判断要寻找的 K 是否在(left,right] ,不在就根据情况再从[from, left] 或 (right, end] 中寻找。
另:
此处找的是第K大是包含重复元素的,同时为了使方法平均运行时长更稳定每次都随机取数组中一个元素为基准,期望平均时间复杂度为 O(n)。此外还可以使用堆排序 时间复杂度O(nlogn)。
LeetCode 相关练习: 215. 数组中的第K个最大元素 、1738. 找出第 K 大的异或坐标值