题目描述
小T 是一名质量监督员,最近负责检验一批矿产的质量。这批矿产共有 nn 个矿石,从 11到nn 逐一编号,每个矿石都有自己的重量 w_iw**i 以及价值v_iv**i 。检验矿产的流程是:
1 、给定mm个区间[L_i,R_i][L**i,R**i];
2 、选出一个参数WW;
3 、对于一个区间[L_i,R_i][L**i,R**i],计算矿石在这个区间上的检验值Y_iY**i:
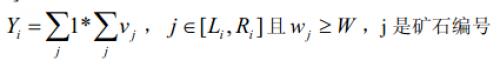
这批矿产的检验结果YY 为各个区间的检验值之和。即:Y_1+Y_2...+Y_mY1+Y2...+Y**m
若这批矿产的检验结果与所给标准值SS 相差太多,就需要再去检验另一批矿产。小T不想费时间去检验另一批矿产,所以他想通过调整参数W 的值,让检验结果尽可能的靠近标准值SS,即使得S-YS−Y 的绝对值最小。请你帮忙求出这个最小值。
解析
看到区间操作,首先想到可能数据结构,但是我一看。数据范围吓人,如果你一定要用的话,祝您线段树过百万。
分析题目,我们需要求一个限制条件的最小值,很容易想到二分答案。看到题述公式,经验告诉我们这个式子可以分开求,也就是每次check时求一组满足(w_j>W)的(m)个询问的(sum_j1)和(sum_jv_j),然后乘起来就得到答案。但是(O(nm))的求肯定会爆掉,我们就自然而然地考虑一个前缀和的优化,减少大量计算。
参考代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<vector>
#define INF 999999999999
#define PI acos(-1.0)
#define N 200010
#define MOD 2520
#define E 1e-12
#define ll long long
using namespace std;
inline ll read()
{
ll f=1,x=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
inline ll max(ll x,ll y){return x>y?x:y;}
inline ll min(ll x,ll y){return x<y?x:y;}
ll n,m,S;
int l[N],r[N],w[N],v[N];
ll tmp1[N],tmp2[N];
ll res;
inline bool check(int x)
{
res=0;
for(int i=1;i<=n;++i){
tmp1[i]=tmp2[i]=0;
if(w[i]>=x) tmp1[i]=tmp1[i-1]+1,tmp2[i]=tmp2[i-1]+v[i];
else tmp1[i]=tmp1[i-1],tmp2[i]=tmp2[i-1];
}
for(int i=1;i<=m;++i)
res+=(tmp1[r[i]]-tmp1[l[i]-1])*(tmp2[r[i]]-tmp2[l[i]-1]);
if(res-S==0){printf("0
");exit(0);}
if(res-S>0) return 1;
else return 0;
}
int main()
{
n=read(),m=read(),S=read();
ll maxx=-1,minn=INF;
for(int i=1;i<=n;++i){
w[i]=read(),v[i]=read();
minn=min(minn,w[i]),maxx=max(maxx,w[i]);
}
for(int i=1;i<=m;++i) l[i]=read(),r[i]=read();
ll l=minn-1,r=maxx+1;
ll ans=0x3f3f3f3f3f3f3f3f;
while(l<r){//据说只有10%的程序员写的对二分(摊
int mid=(l+r+1)>>1;
if(check(mid)) l=mid;
else r=mid-1;
res=llabs(res-S);//注意longlong类型的绝对值函数要用这个,否则会溢出
ans=min(ans,res);//找最优解
}
printf("%lld
",ans);
return 0;
}