题目描述
Black Box是一种原始的数据库。它可以储存一个整数数组,还有一个特别的变量i。最开始的时候Black Box是空的.而i等于0。这个Black Box要处理一串命令。
命令只有两种:
ADD(x):把x元素放进BlackBox;
GET:i加1,然后输出Blackhox中第i小的数。
记住:第i小的数,就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如:
我们来演示一下一个有11个命令的命令串。(如下图所示)
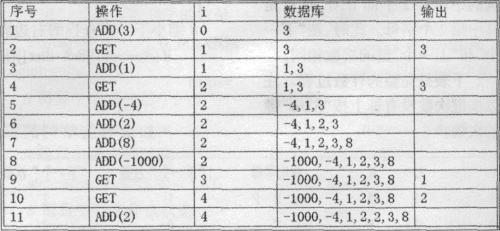
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串:
1.A(1),A(2),…A(M):一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数,M$200000。例如上面的例子就是A=(3,1,一4,2,8,-1000,2)。
2.u(1),u(2),…u(N):表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(l,2,6,6)。输入数据不用判错。
解析
我一看,动态维护第k小,这不是对顶堆模板吗。
简单讲一下:对于一个递减的序列,长度为(n),其中的值可以分为两部分:第(1sim k)大的数为一部分,第(k+1sim n)大数为第二部分 。对顶堆,就是用堆维护这两部分的数。我们不妨用一个大根堆维护(1sim k),用一个小根堆维护(k+1sim n),这样,第(k)小的数和第(k+1)小的数都恰好在堆顶,在输出时我们输出大根堆的堆顶就行了。这也是为什么这个方法叫对顶堆。
实现起来简单又快捷,优先队列就可以了。
参考代码
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#define ll long long
#define N 200010
using namespace std;
inline int read()
{
int f=1,x=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
priority_queue<ll> Q;
priority_queue<ll,vector<ll>,greater<ll> > q;
int k,a[N],b[N],n,m;
int main()
{
m=read(),n=read();
for(int i=1;i<=m;++i) a[i]=read();
for(int j=1;j<=n;++j) b[j]=read();
k=1;
Q.push(a[1]);
for(int i=1;i<=m;++i){
if(i>1){
if(a[i]>Q.top()) q.push(a[i]);
else Q.push(a[i]);
}
while(i==b[k]){
while(Q.size()>k) q.push(Q.top()),Q.pop();
while(Q.size()<k) Q.push(q.top()),q.pop();
++k,printf("%d
",Q.top());
}
}
return 0;
}