哈希表
哈希表就是一种以 键-值(key-indexed) 存储数据的结构,我们只要输入待查找的值即key,即可查找到其对应的值。
哈希的思路很简单,如果所有的键都是整数,那么就可以使用一个简单的无序数组来实现:将键作为索引,值即为其对应的值,这样就可以快速访问任意键的值。这是对于简单的键的情况,我们将其扩展到可以处理更加复杂的类型的键。
使用哈希查找有两个步骤:
- 使用哈希函数将被查找的键转换为数组的索引。在理想的情况下,不同的键会被转换为不同的索引值,但是在有些情况下我们需要处理多个键被哈希到同一个索引值的情况。所以哈希查找的第二个步骤就是处理冲突
- 处理哈希碰撞冲突。有很多处理哈希碰撞冲突的方法,如拉链法和线性探测法。
哈希表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制,那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1);如果没有时间限制,那么我们可以使用无序数组并进行顺序查找,这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。
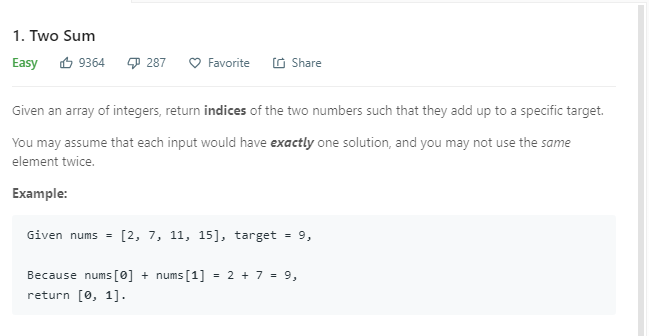
001.Two Sum
解题思路
这里需注意,返回值为[index_a,index_b],内部都是序列值。这道题用暴力解法行不通,用首尾递进的解法,时间复杂度为O(nlogn)。用哈希表可以达到最佳效果。
代码
这是个人用哈希表解决
class Solution:
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
dNums = {}
for i, n in enumerate(nums):
dNums[n] = i
for i, n in enumerate(nums):
m = target - n
if m in dNums.keys() and i != dNums[m]:
return [i, dNums[m]]
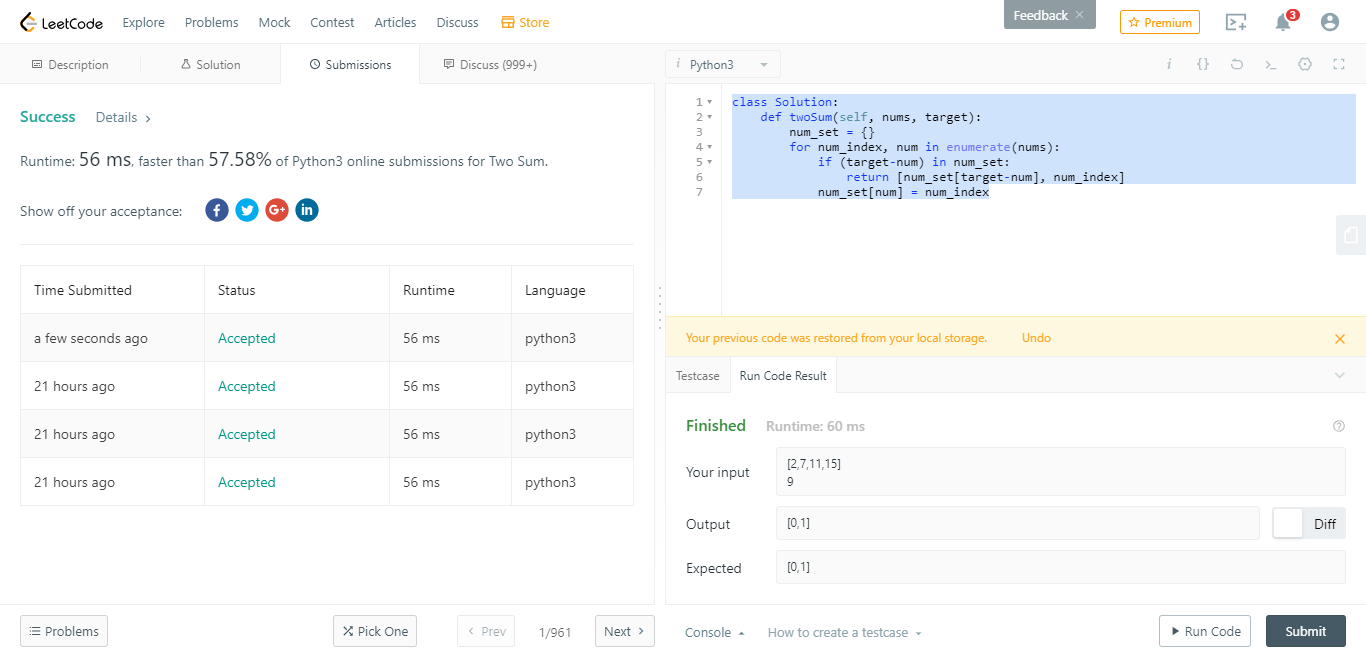
上面理论上的时间复杂度为O(2n),实际上和首尾递进的解法差不多了。这里,答案告诉我们存在O(n)的解法,如下:
class Solution:
def twoSum(self, nums, target):
num_set = {}
for num_index, num in enumerate(nums):
if (target-num) in num_set:
return [num_set[target-num], num_index]
num_set[num] = num_index
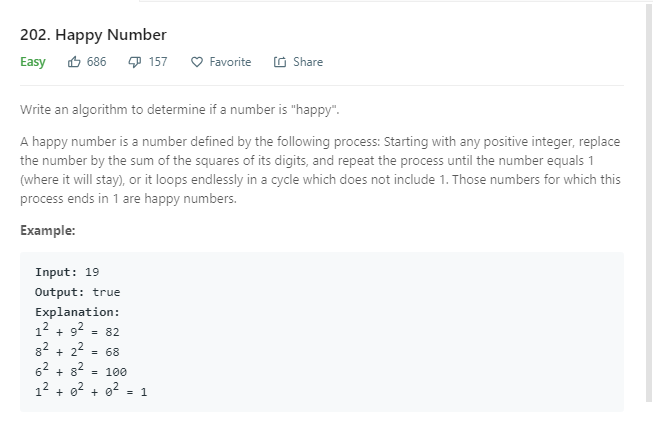
202.Happy Number
解题思路:
这道题要求我们取Number上的各位数字的平方并相加。从这个条件里,可以很快反应到,19和91在本题里是没有差别的。
然后,在自己额外造用例时发现,一些数字会产生自循环,如58-89-145-42-2-4-16-37-58,这种数字肯定不是HpNnum。
通过上面的规律探索,可以开始思考代码流程。代码的思路很简单,一边算一边存,如果算出来的结果和之前重复,返回False;如果最终得到1,则返回True。
代码
这是我用哈希表写出来的
class Solution:
def isHappy(self, n):
"""
:type n: int
:rtype: bool
"""
hashmap = {}
n_lst = [int(i) for i in str(n)]
while n_lst not in hashmap.values():
hashmap[index] = n_lst
n = sum([i**2 for i in n_lst])
n_lst = [int(i) for i in str(n)]
if n_lst == [1]:
return True
else:
return False
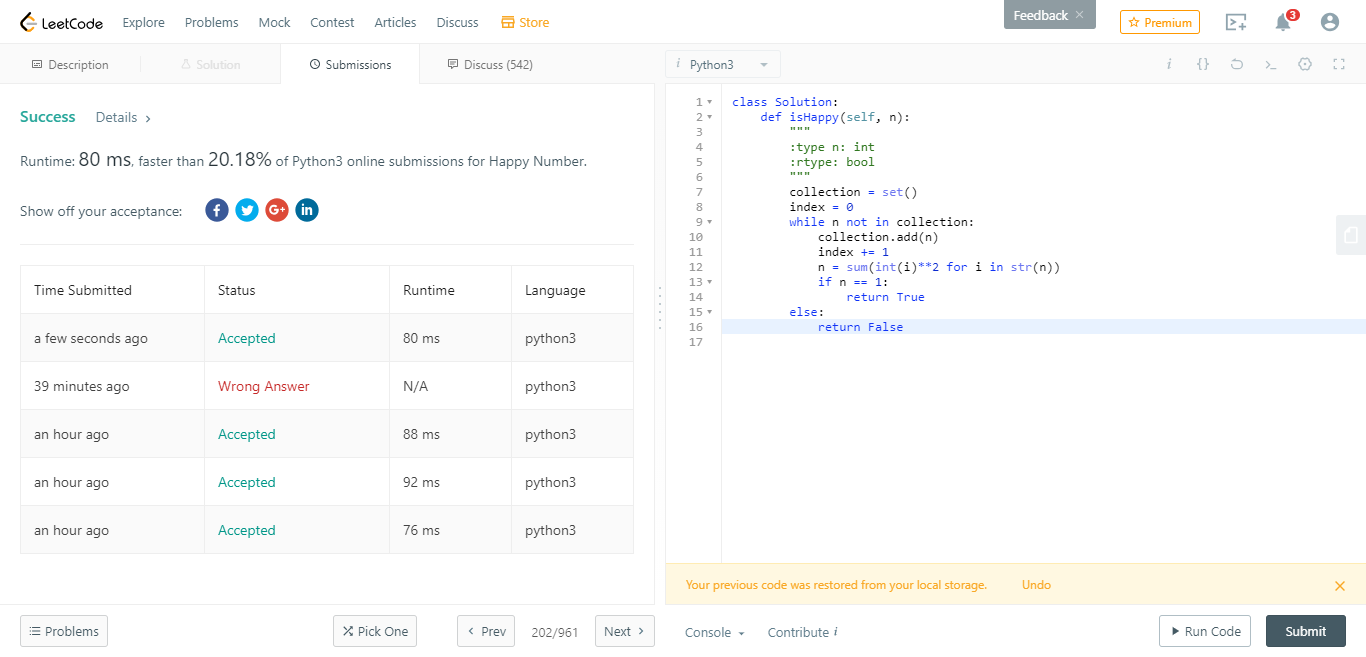
上面有很多值得优化的地方,不过最值得优化的重点不是这个,是用哈希表明显浪费了一半的内存空间。这道题可以用集合会更好。整体优化过的代码如下:
class Solution:
def isHappy(self, n):
"""
:type n: int
:rtype: bool
"""
collection = set()
while n not in collection:
collection.add(n)
n = sum(int(i)**2 for i in str(n))
if n == 1:
return True
else:
return False